数学
充分条件和必要条件
充分条件
A是B的充分条件(多因一果,多个原因都能单独地导致这一后果)
1)有前项必有后项:
2)无前项时可能有后项也可能没有,但都不影响前项是后项的充分条件- 必要条件
前项是后项的必要条件(合因一果,多个原因共同作用导致这一结果)

缺少任何一个原因都不能导致这一后果(无前项一定无后项)所以也可认为前项假后项真这个命题为假
汉语
”的“ ”地“的区别
的
判断技巧
如果“的”后面的词语是名词(或可补出名词),则用“的”。例子:
这本书是老师的。(“的”代替省略的名词“书”)
地
判断技巧
如果“地”后面的词语是动词或形容词(表示动作/状态),则用“地”。
**例子:**
认真地学习(副词+地+动词)
开心地笑了(形容词+地+动词)
出奇地安静(副词+地+形容词)
牛顿迭代法求平方根
该方法主要思想就是切线是曲线的线性逼近。
假设我们要求一个数的平方根(a),那么可以写为一个函数:
在f(x)上任意一点

微分和导数的关系
参考链接:https://www.zhihu.com/question/22199657/answer/115178055
从历史角度来看,微积分被发明了两次,古典微积分和极限微积分。古典微积分存在一定的缺陷,极限微积分弥补了这个缺陷,也是目前一直在使用的。
古典微积分
导数的出现不是牛顿和莱布尼兹发明的,之前数学家已经在对曲线的切线进行研究了,但是牛顿和莱布尼兹在解决曲面下面积的时候把导数的定义确定下来了。
曲线下的面积
曲线下的面积在微积分出现之前是一个很复杂的问题,微积分求解的主要思想是把曲线下的面积划分成了无数个矩形面积之和:
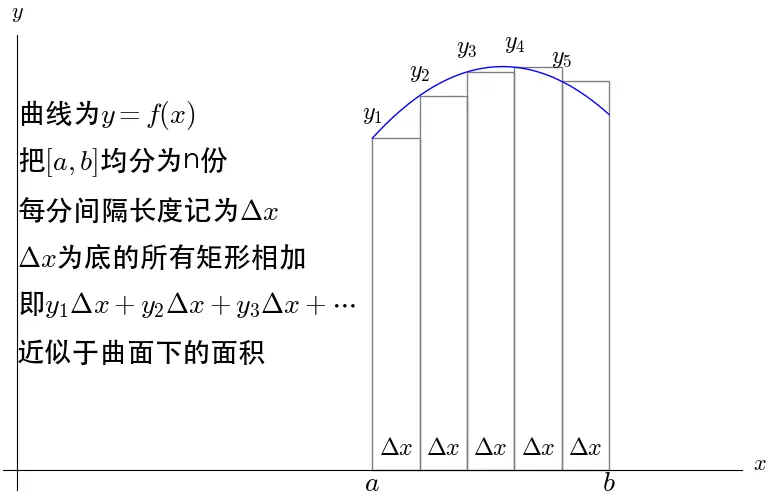
直觉告诉我们,如果
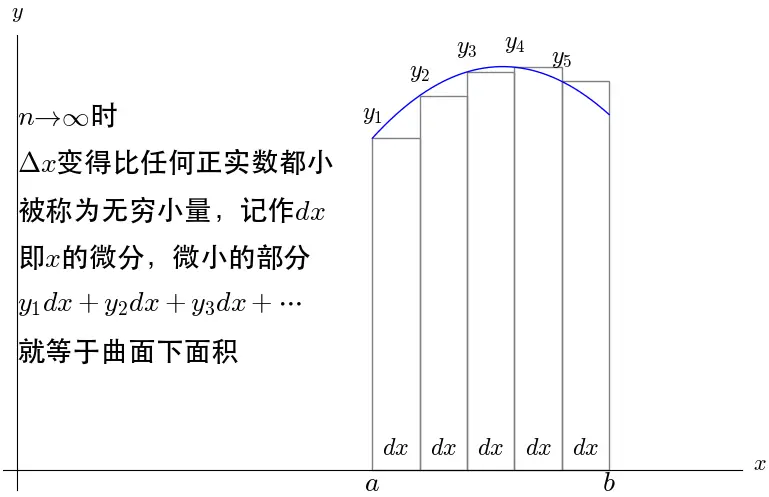
无穷小量就在这里出现了,无穷小量是建立微积分的基础,莱布尼兹介绍微积分的论文就叫做《论深度隐藏的几何学及无穷小与无穷大的分析》。在当时的观点下,无穷小量到底是什么也是有争论的,当时有数学家打比喻:“无穷小量就好比山上的灰尘,去掉和增加都没有什么影响”,很显然有人认为这是真实存在的。
在具体计算曲面下面积,即我们现在所说的定积分的时候,必然会遇到导数的问题,所以很自然的开始了对导数的定义和讨论。
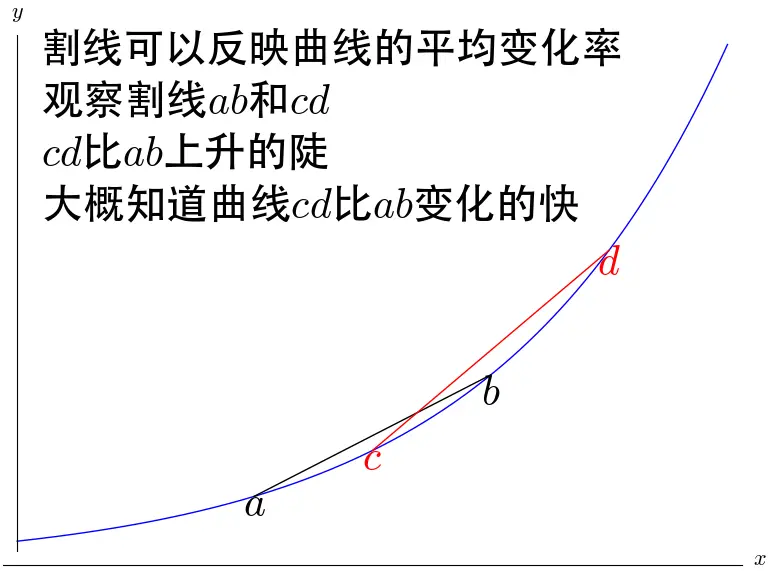
割线可以反应曲线的平均变化率,也就是说这一段大概总的趋势是上升还是下降,上升了多少,但是并不精确。
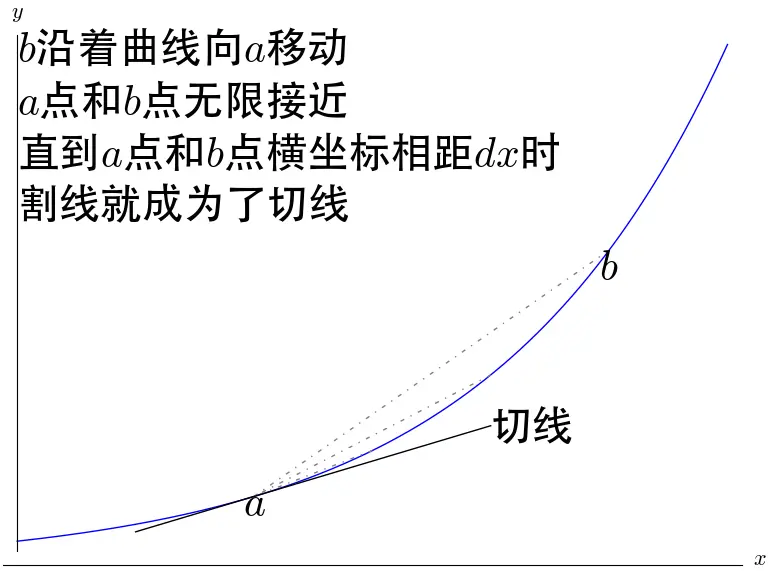
有了切线之后我们进一步去定义导数:
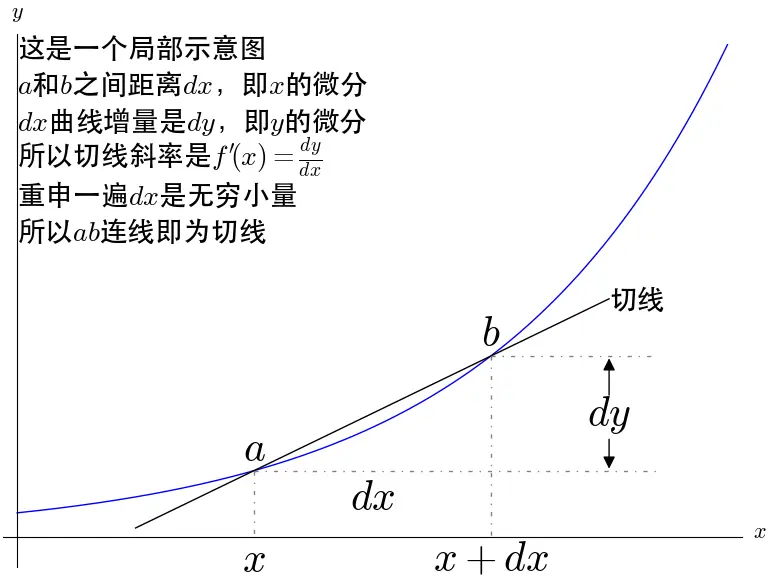
从上图就可以得到导数的定义:
无穷小量的麻烦
上一节的图实际上是有矛盾的:
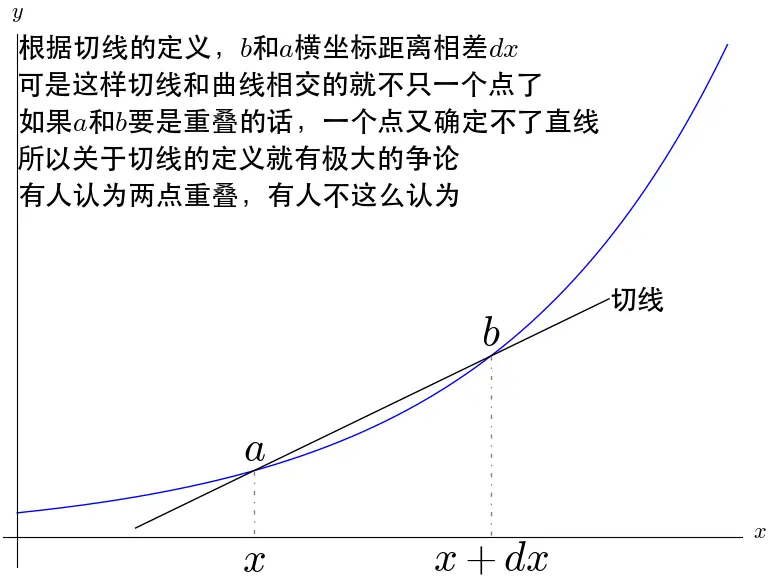
所以就切线的定义而言,微积分的基础就是不牢固的。
无穷小量的麻烦还远远不止这一些,
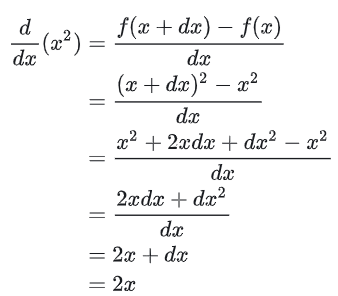
仔细看看运算过程,
无穷小量和无穷小量相除为什么可以得到不一样的值?难道不应该都是1?
小结
切线:通过无穷小量定义了切线
导数:导数就是切线的斜率
微分:微分是微小的增量,即无穷小量
导数、微分的正确定义(极限微积分)
极限微积分下,先发明极限,用极限去定义导数。再使用导数去定义微分。
基于极限重建微积分
莱布尼兹、欧拉等都认识到了无穷小量导致的麻烦,一直拼命想要修补,但是这个问题要等到200年后,19世纪极限概念的清晰之后才得到解决。
解决办法是,完全摈弃无穷小量,基于极限的概念,重新建立了微积分。
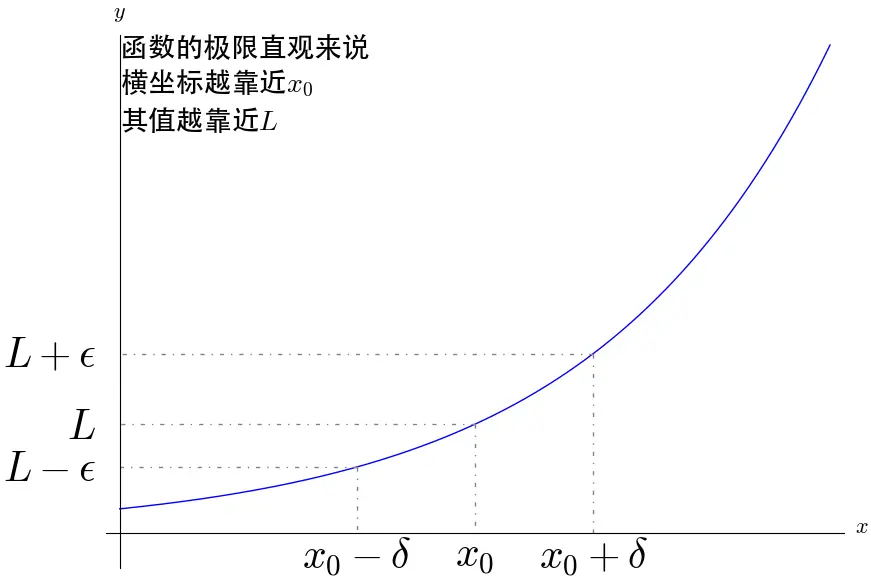
导数的定义:
接下来通过导数去定义微分:
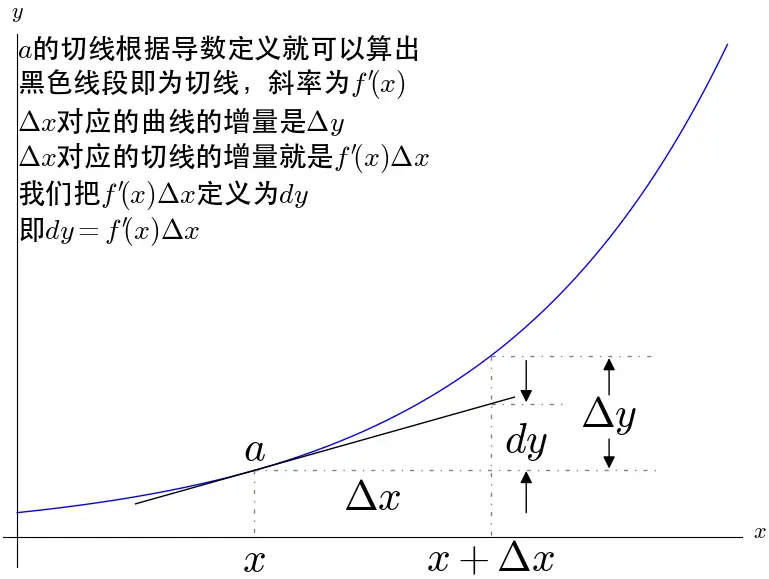
令
最后可以得到
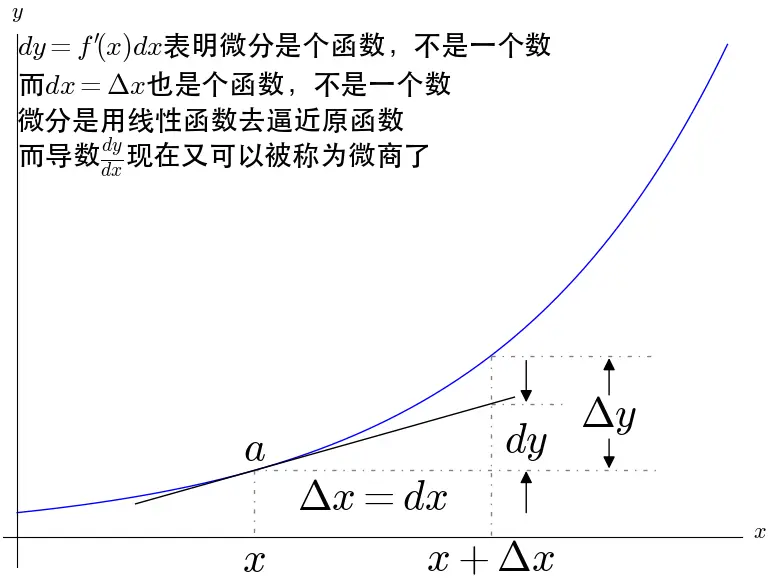
小结
导数:被定义为一个极限,其意义就是变化率
微分:是一个线性函数,其意义就是变化的具体数值
切线:有了导数之后就可以被确定下来了
古典微积分与极限微积分的对比
- 古典微积分是先定义微分再定义导数,极限微积分是先定义导数再定义微分。
- 古典微积分的导数是基于无穷小量定义的,极限微积分的导数是基于极限定义的。
- 古典微积分的微分是无穷小量,极限微积分的微分是一个线性函数。
- 古典微积分的定积分是求无穷小矩形面积的和,极限微积分的定积分是求黎曼和。
- 古典微积分的切线是可以画出来的,极限微积分的切线是算出来的。古典微积分的建立过程很直观,极限微积分的建立过程更抽象。
其他问题
。在古典微积分中可以理解为消去,但是在极限微积分中我们应该认识到,这两个 实际上是不同的函数。 古典微积分中, 确实表明是无穷多个矩形的底边,消去也是合理的,而极限微积分中, 是求黎曼和,我们可以把 当作左括号, 当作右括号,就好比(2+6)=8,计算完毕之后,括号自然就消失了。 - 古典微积分其实已经被摒弃了,我们应该知道这一点,重新从极限的角度去认识微积分。
生活
手机拍照专业模式
【【小米13Ultra】相机专业模式不会用?进来看看,包教包会!】
以小米系列手机为例,可以调节的参数依次有:
- WB
白平衡。能够调节画面的冷暖调。尽量不要动这个参数,自动就好。即使要调节,也可以通过调节色温来矫正色彩。 - F
对焦。(在设置对焦前,建议把上方菜单栏中的峰值对焦打开,以辅助我们查看画面中的焦点位置)。可以让我们将焦点放到想拍摄的物体。 - S
快门速度。快门动作可以理解为眨眼,快门速度可以理解为眨眼的速度。快门速度越短,进光量小,画面越暗;快门速度越快则反之。 - ISO
感光度。感光度越低,画质越暗,画面越清晰;感光度高则反之。 EV
曝光补偿。想让画面越亮或越暗,直接设置曝光补偿。如果想拍摄白云或白雪,可以增加。如果拍摄黑色的景物或场景,可以降低。总结:大部分的时候都设置为自动挡,改的最多的为快门和曝光补偿,有需要再改。
win10操作
遇到的问题
desktopwindowxamlsource窗口
某一次在任务栏下面出现了“desktopwindowxamlsource“字样的东西,点击没反应,如果右键关闭,那么onedirve也会被关闭。卸载onedrive,重新安装,一开始可以,但几天后又出现了。
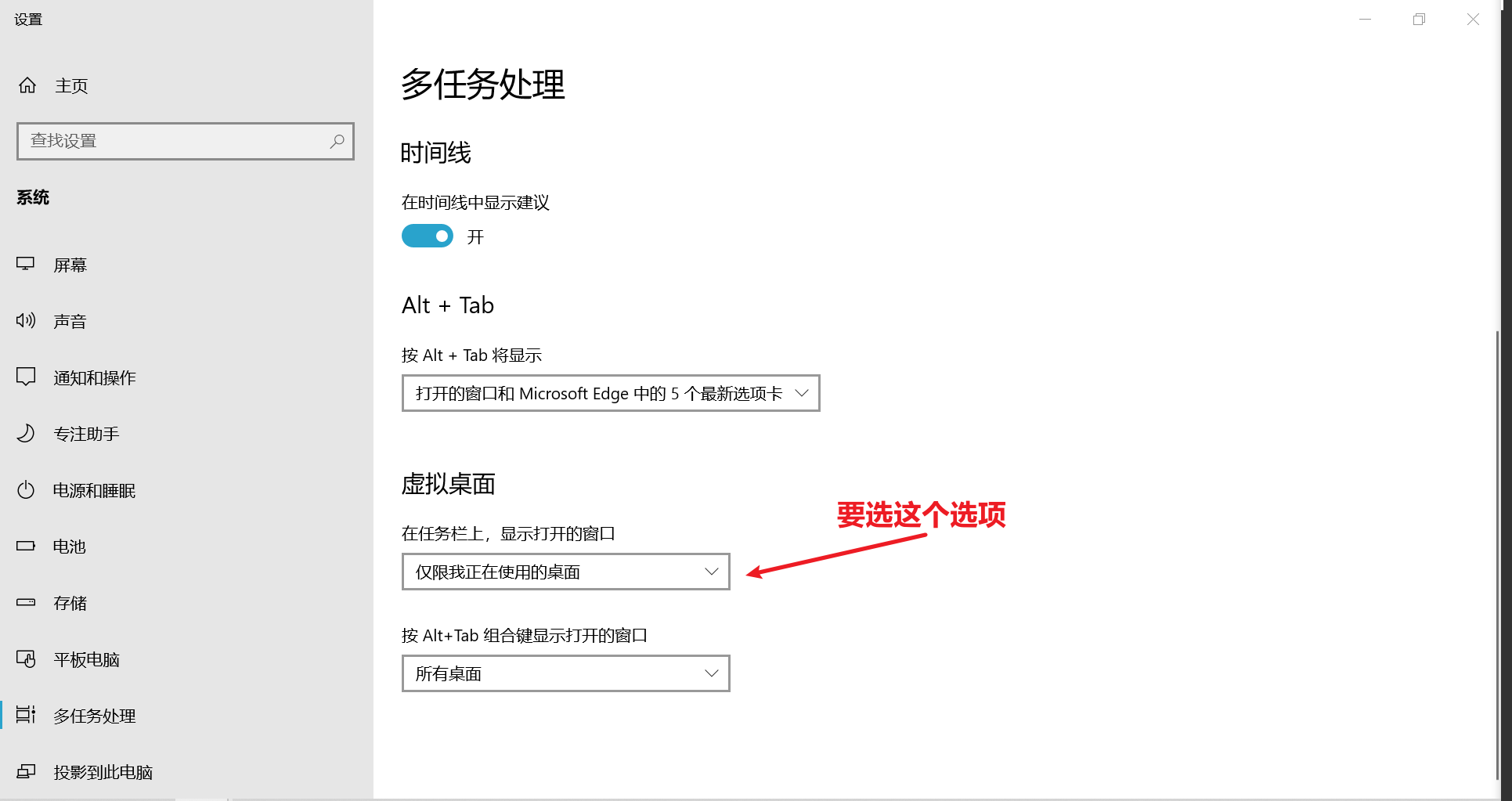
*解决方法:
设置->搜索多任务处理->虚拟桌面。“在任务栏上,显示打开的窗口”。选择“仅限我正在使用的电脑”
Windows 10每天定时执行脚本
Windows键+R 调出此窗口,输入compmgmt.msc (调用的是计算机管理)
原文链接
点击下面的框,创建一个基本任务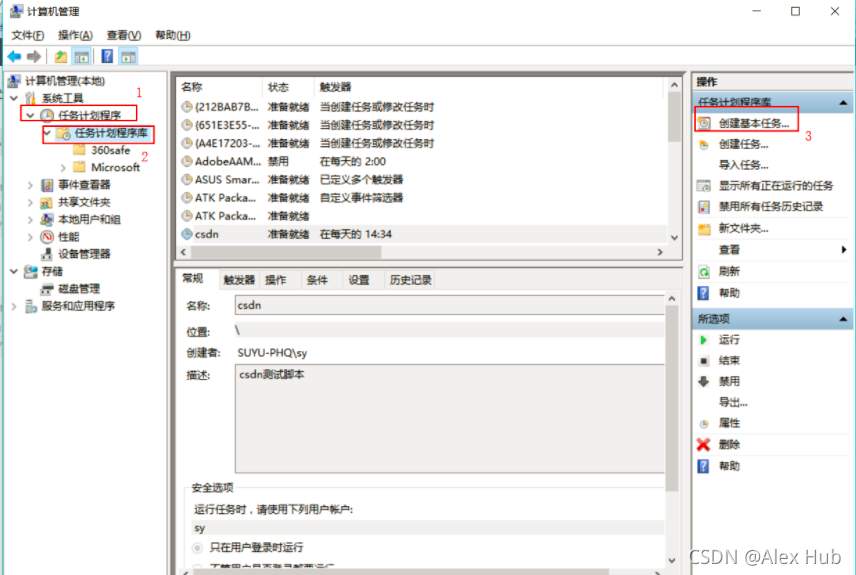
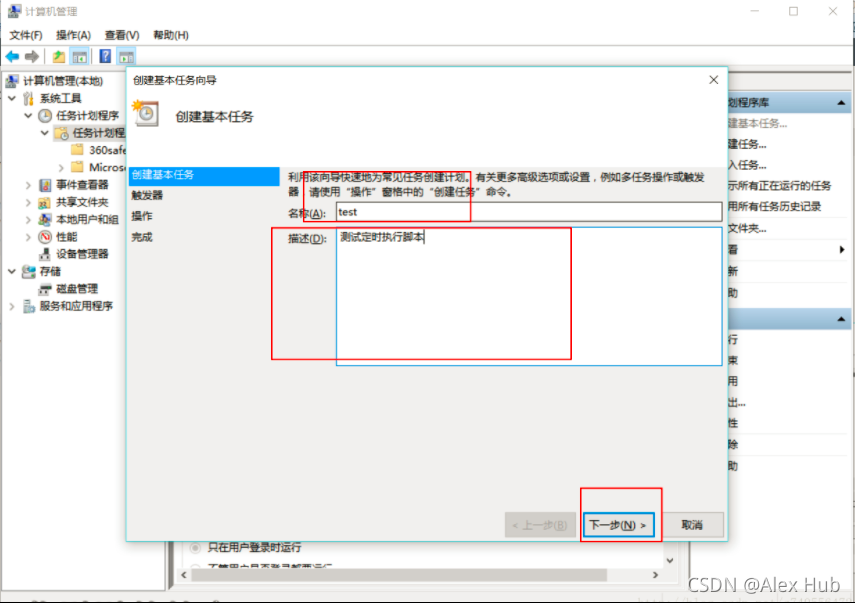
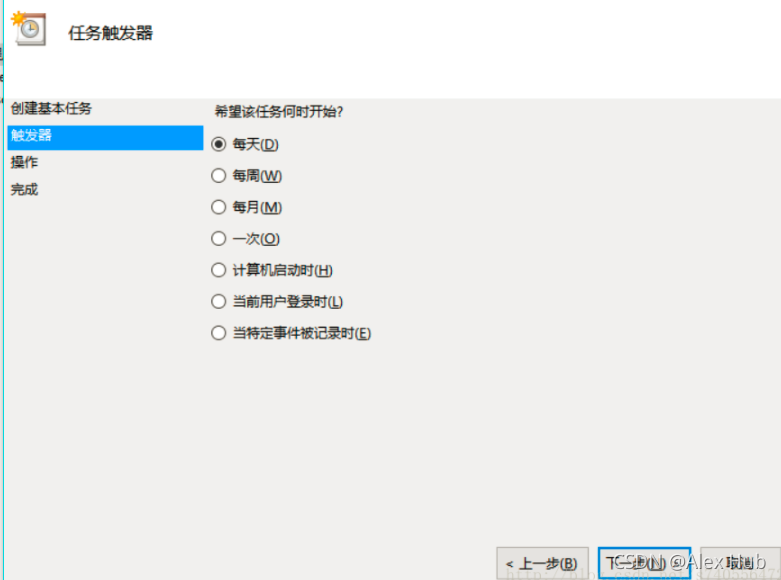
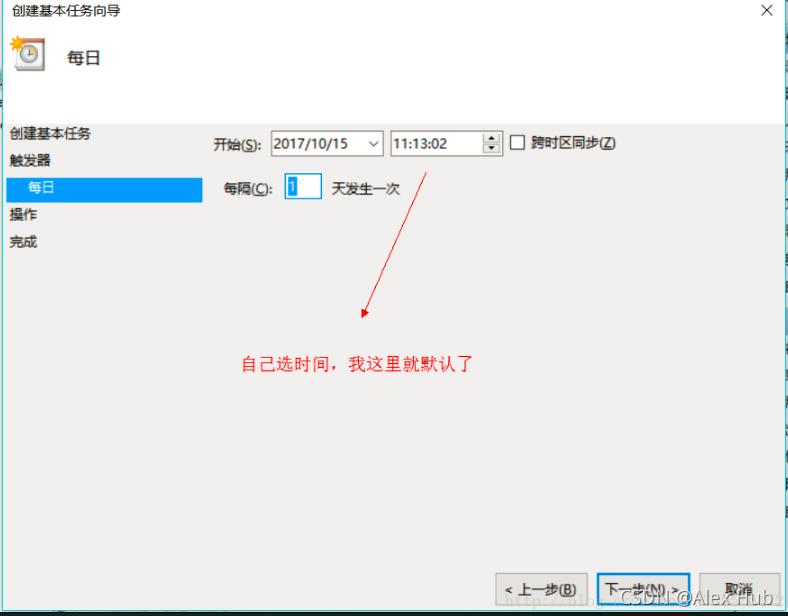
后面跟着点就好
Windows重启打印机服务
有时候需要重启打印机,采用命令行的方式。
Win+R :services.msc 找到 Print Spooler 重启。
Win10开机自启动软件
把该应用程序的快捷方式放到“系统启动文件夹”里;
C:\ProgramData\Microsoft\Windows\Start Menu\Programs\StartUp
Win10查看电脑配置信息和型号
使用dxdiag命令检查电脑配置
按下键盘上的Win+R组合键,打开运行窗口,输入dxdiag,点击确定。
在打开的页面中就可以看到当前计算机名称、操作系统、CPU、内存等重要信息。
使用diskmtgt.msc命令进入磁盘管理,查看硬盘大小及已使用的空间。
465.76GB就是500G的硬盘,不要怀疑是不是奸商给你的是假货,这是没有问题的,硬盘的生产厂家在生产硬盘时用的是1000进制,即1GB=1000MB;1MB=1000KB;1KB=1000B。而电脑的计算进制是1024,即1G=1024MB;1MB=1024KB;1kB=1024B,这样就会造成电脑检测出来的容量比标称容量小。
此外,除了以上方法也可以进入设备管理器里查看电脑配置信息,步骤:右击桌面上的“计算机”—>“设备管理器”,在设备管理器中就可以看见电脑配置情况了
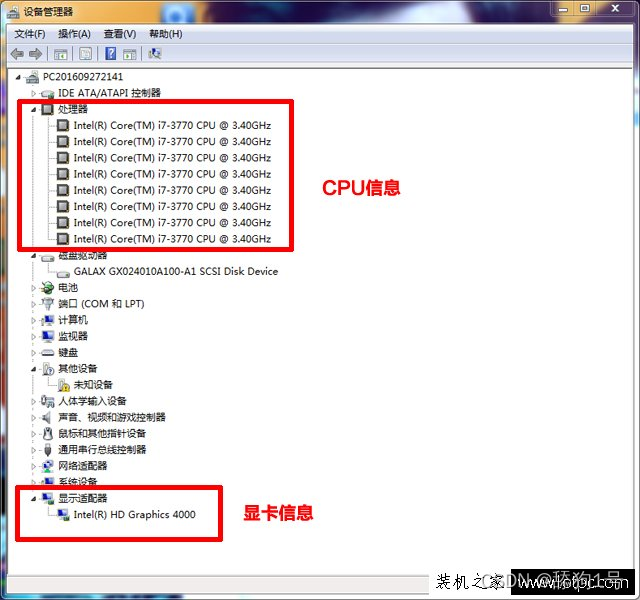
win10查看端口使用情况
netstat [选项]
具体选项可自主查询使用示例:
netstat -a # 列出所有端口
netstat -at # 列出所有TCP端口
netstat -au # 列出所有UDP端口
netstat -ax # 列出所有unix端口
netstat -atnlp # 直接使用ip地址列出所有处理监听状态的TCP端口,且加上程序名
netstat -ano # 端口+显示ip+显示计时器
netstat -ano |findstr "端口号" #这个端口被哪个应用占用,实际输入端口号需要用引号括起来
tasklist |findstr "进程id号" #查看到对应的进程id之后,就可以通过id查找对应的进程名称
taskkill /f /t /im "进程id或者进程名称" #通过命令杀掉进程,或者是直接根据进程的名称杀掉所有的进程录屏
win10/win11自带的我觉得不好用,选择用QQ自带的。启动QQ的录屏可以去“设置-快捷键”里面查看。我这里看到的是”Ctrl+Alt+R”。
win11内存占用高
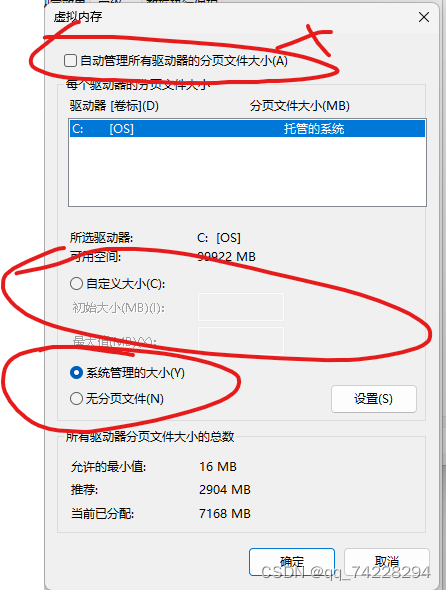
16g的内存,打开电脑,只开启了几个页面内存占用率就是90%左右。尝试了几个办法,最有用的是设置虚拟内存。
原链接:https://blog.csdn.net/qq_74228294/article/details/138399843
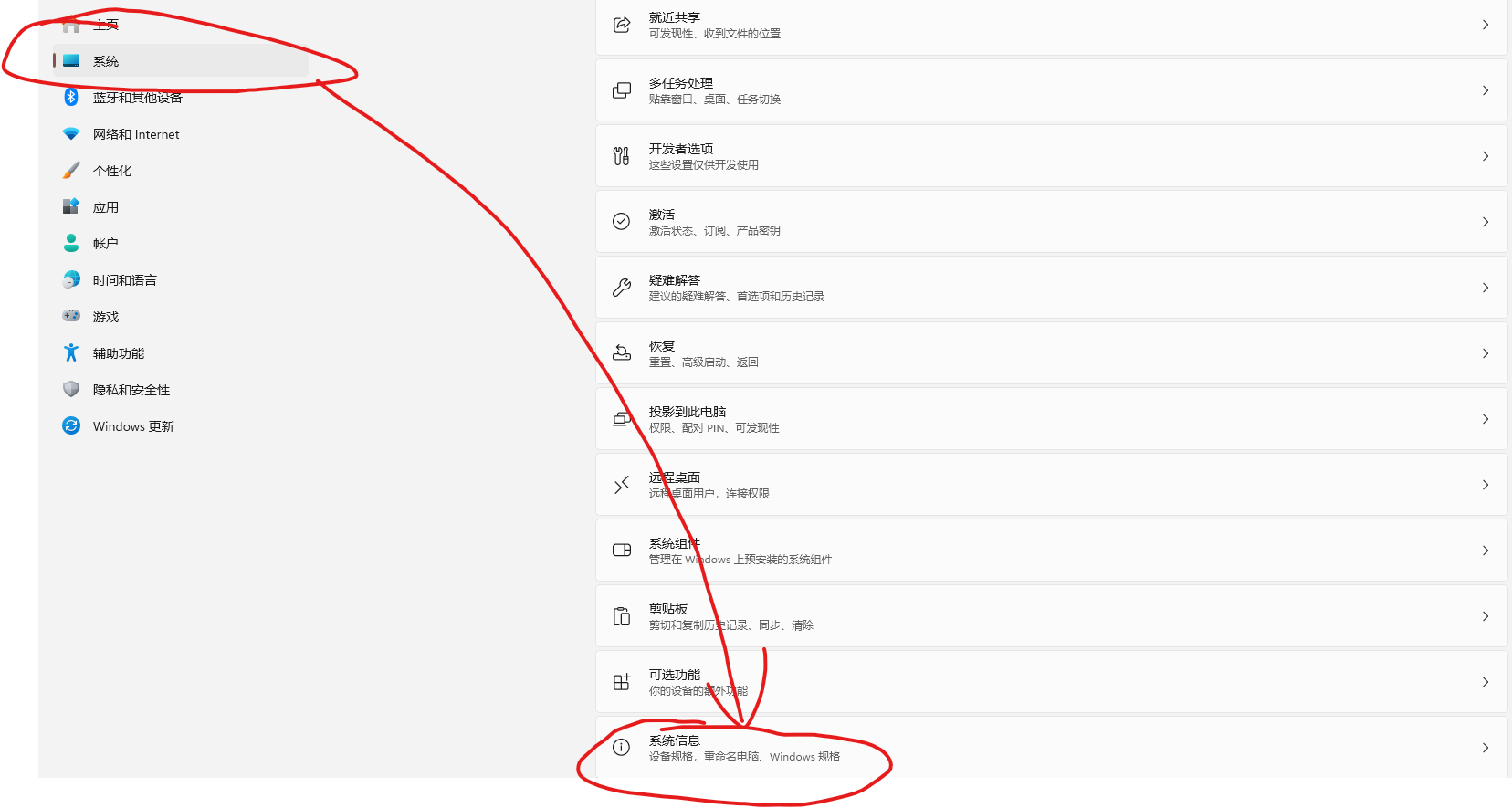
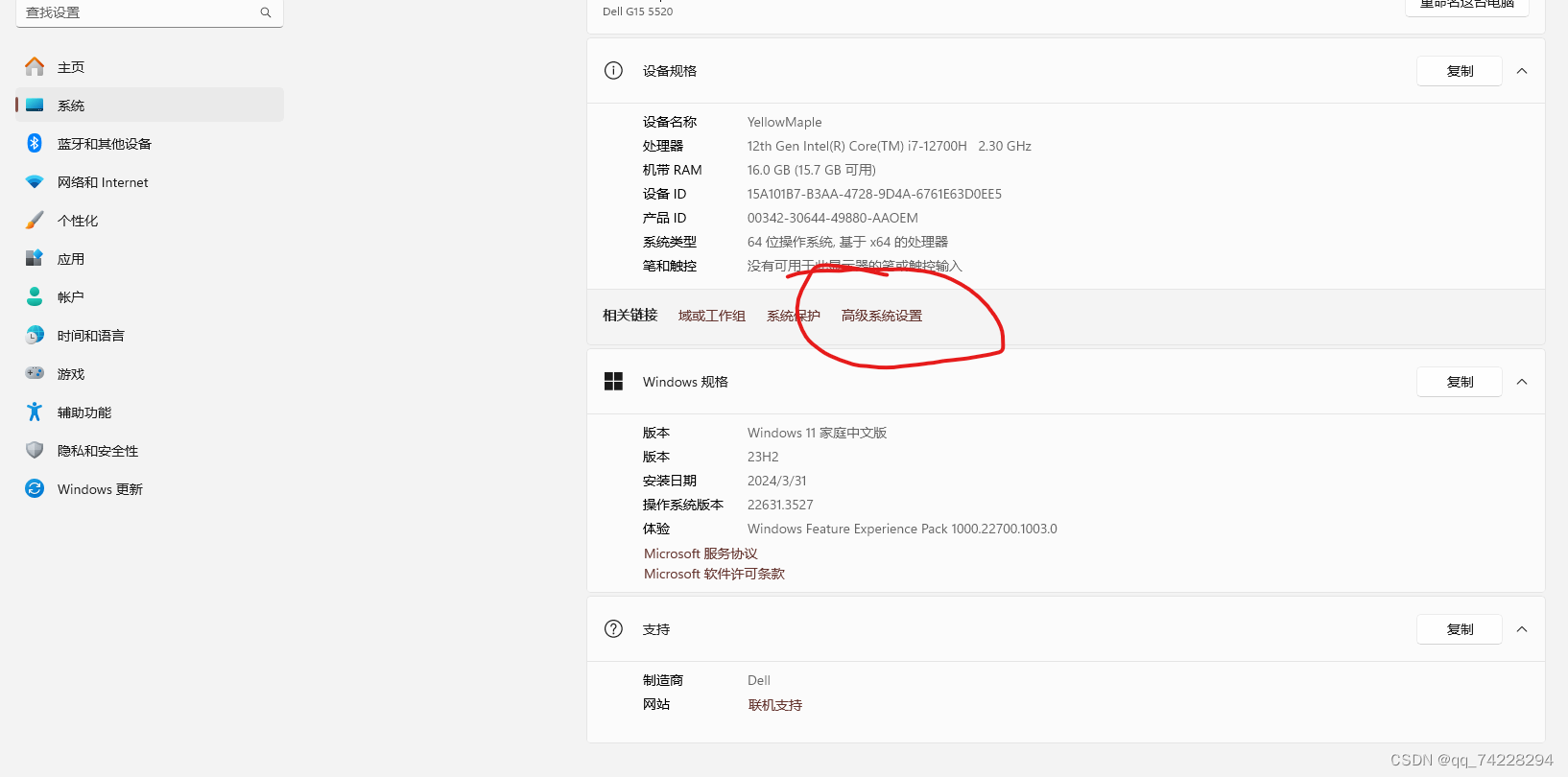
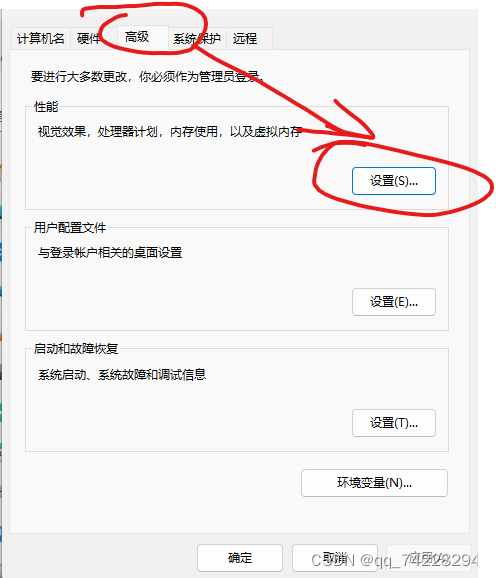
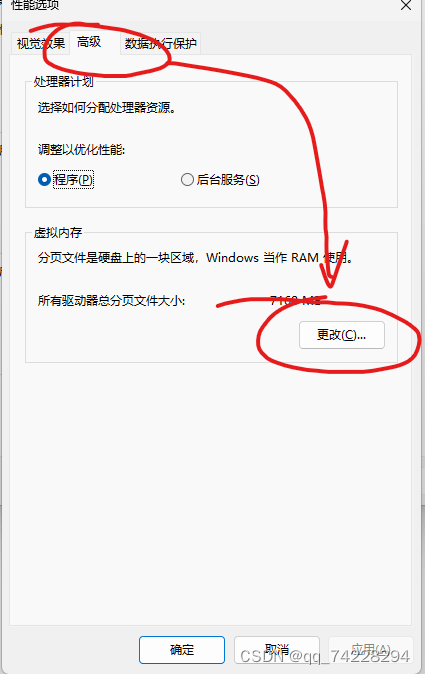
先取消勾选“自动管理分页大小”。下面的“自定义大小”是根据自己的内存来设置,拿不准就网上搜索。或者不勾选“自定义大小”,直接勾选下方的“系统管理的大小”。我就是勾选的“系统管理的大小”
由于此设备上的安全设置已更改,你的pin码不再可用
这种情况一般发生在把硬盘拷贝后,或者直接把硬盘拿到新的设备上时发生。
- 长按 Shift 键的同时点击重启
- 重启后进入到高级启动界面,点击:疑难解答 - 高级选项 - 命令提示符
- 用命令提示符将 utilman.exe 换为 cmd.exe
- Utilman是Windows辅助工具管理器,在登陆界面是可以直接调用的。
move c:\windows\system32\utilman.exe c:\ && copy c:\windows\system32\cmd.exe c:\windows\system32\utilman.exe。这里面的windows有可能是Windows,不过可以用table来补齐,大小写不对没有关系,字母正确就可以。完成后重启。
- Utilman是Windows辅助工具管理器,在登陆界面是可以直接调用的。
- 修改注册表的值
- 点击右下角小人形状的按钮,即可弹出命令提示符界面。在命令提示符界面中输入 regedit 再回车,即可打开注册表编辑器。

- 找到:\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows NT\CurrentVersion\PasswordLess\Device。将“DevicePasswordLessBuildVersion”的值修改为“0”(十六进制)
- 点击右下角小人形状的按钮,即可弹出命令提示符界面。在命令提示符界面中输入 regedit 再回车,即可打开注册表编辑器。
- 重启后。选择密码登录,即可成功登入系统。在设置中,先删除 PIN 的设置,注销系统后,再添加 PIN 的设置。打开注册表编辑器,再把 DevicePasswordLessBuildVersion”的值改回“2”。
- C盘根目录的utilman.exe剪切到c:\Windows\System32\下覆盖即可
mathtype
mathtype试用期到期 解决办法
- win + R 打开运行窗口,输入regedit
- 找到注册表.计算机\HKEY_CURRENT_USER\SOFTWARE\Install Options
- 删掉options6.9
mathtype为word中的公式自动编号
bat脚本
案例1:拉取代码
cmd /k "cd /d 执行目录&&git pull origin dev1:dev1&&cd /d 执行目录&&git pull origin hexo:hexo"&& 表示前面的执行完才会执行后面的
执行目录要替换为具体的路径。
win 11 添加VSCode至右键菜单
- 新建一个文本文件,内容如下:
Windows Registry Editor Version 5.00 [HKEY_CLASSES_ROOT\*\shell\VSCode] @="Open with Code" "Icon"="S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe" [HKEY_CLASSES_ROOT\*\shell\VSCode\command] @="\"S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe\" \"%1\"" Windows Registry Editor Version 5.00 [HKEY_CLASSES_ROOT\Directory\shell\VSCode] @="Open with Code" "Icon"="S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe" [HKEY_CLASSES_ROOT\Directory\shell\VSCode\command] @="\"S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe\" \"%V\"" Windows Registry Editor Version 5.00 [HKEY_CLASSES_ROOT\Directory\Background\shell\VSCode] @="Open with Code" "Icon"="S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe" [HKEY_CLASSES_ROOT\Directory\Background\shell\VSCode\command] @="\"S:\\Microsoft VS Code\\Microsoft VS Code\\Code.exe\" \"%V\"" 将vscode安装地址替换成你实际安装的地址
注意:地址最好使用双斜杠,替换的时候要注意不要删掉其他的东西,上述中需要替换的只有S:\Microsoft VS Code\Microsoft VS Code\Code.exe这个地方将文件后缀名改成 .reg,最后双击执行就成功了。
模糊照片变高清
访问
bigjpg.com
将照片扔上去就好。
右键菜单,用vscode打开文件和文件夹
效果如下: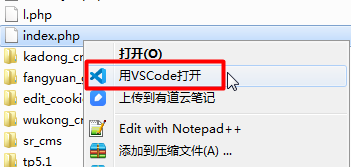
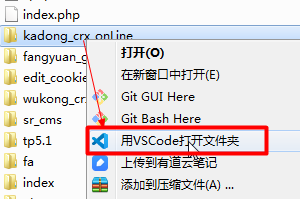
方法1 重装软件
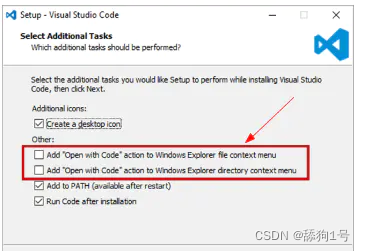
方法2 修改注册表
1.右键打开文件
1, Win+R 打开运行,输入regedit,打开注册表,找到HKEY_CLASSES_ROOT\*\shell分支,如果没有shell分支,则在*下点击右键,选择“新建-项”,建立shell分支。
2, 在shell下新建“VisualCode”项,在右侧窗口的“默认”双击,在数据里输入“用VSCode打开”。这是右键上显示的文字,可以随便写,只是为了方便查看
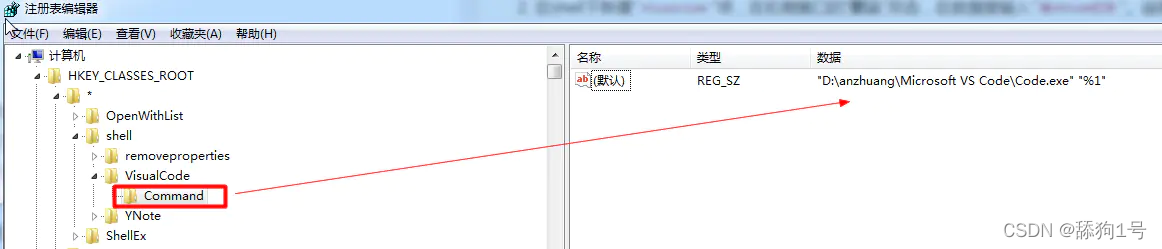
3, 在“VisualCode”下再新建Command项,在右侧窗口的“默认”键值栏内输入程序所在的安装路径,我的是:"D:\anzhuang\Microsoft VS Code\Code.exe" "%1"。其中的%1表示要打开的文件参数。
4, 配置缩略图。在VisualCode项上新建可扩充字符串值,命名为Icon,双击,把"D:\anzhuang\Microsoft VS Code\Code.exe"放进数据就可以了。
5, 关闭注册表,即可生效。
2.右键打开文件夹
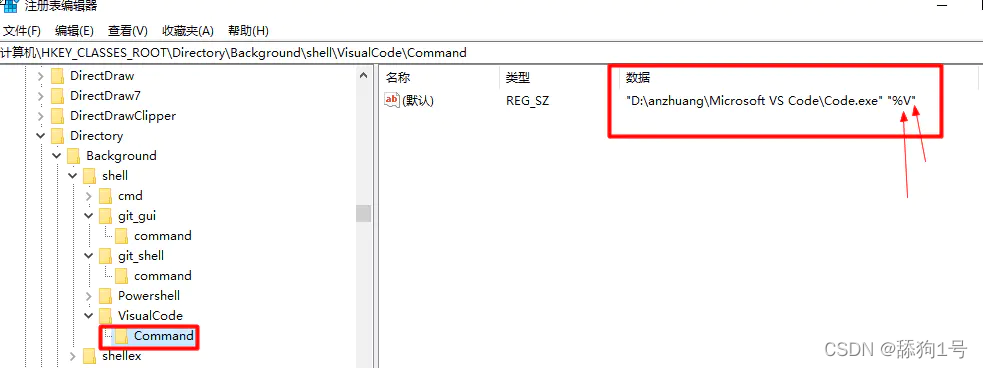
1.Win+R 打开运行,输入regedit,打开注册表,找到HKEY_CLASSES_ROOT\Directory\Background\shell\分支
2、同上面的2完全一样
3、同上,把 %1 改为%V,例如:"D:\anzhuang\Microsoft VS Code\Code.exe" "%V"
4、5同上,完全一样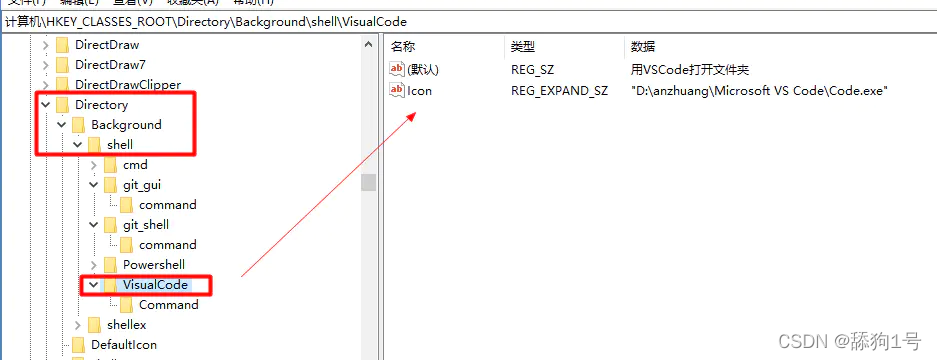
国家推出的标准查询
比如2025-03-28发布的《电动汽车用动力蓄电池安全要求》,可以在下面这个网站查找:
国家标准全文公开系统
专利
如何查询专利
1.登录网站(国家知识产权)
2.专利检索
3.
账号是:1gaofeng1
密码:110
输入申请号查询
Hexo 相关内容
添加自定义的内容
我想给博客添加一些新内容,通过url访问,比如加密功能,但是不希望被模板渲染。
在source目录下新建一个目录,这里取名password,然后把要添加的内容放进去。内容里面要渲染的html文件名为index.html(可以起别的名字)。
然后要在_config.yml里面的”skip_render:”字段里面按固定格式加上文件名,如下图所示。
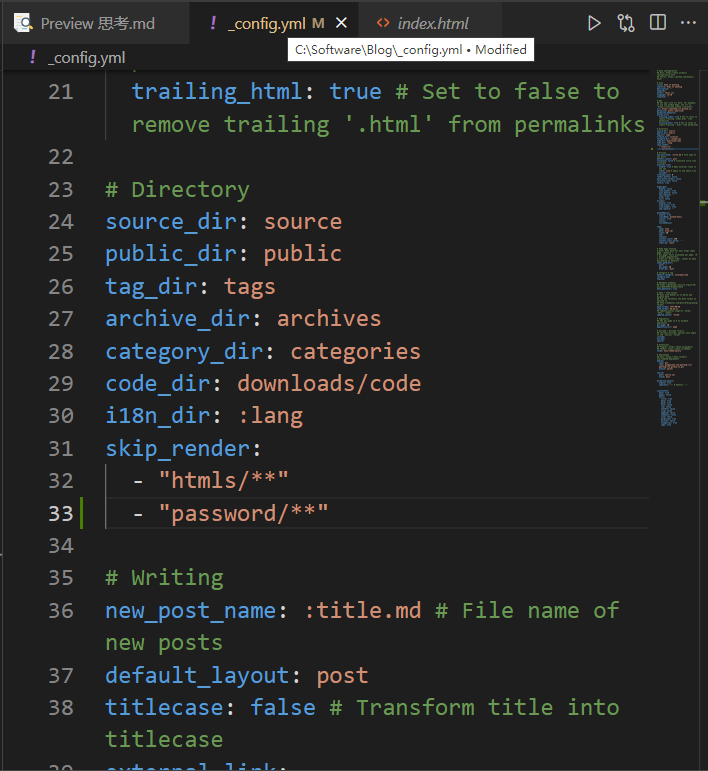
然后提交,访问的时候在url后面跟上
/password/index.html就可以访问对应页面
注意事项
具体的教程网上自行搜索就好,下面重点列出几个容易出问题的地方。
- 仓库名应该为:用户名.http://github.io 这个用户名使用你的GitHub帐号名称代替,这是固定写法。
- hexo配置文件里面的url要换成自己实际访问的url

hexo多终端同步管理
因为hexo只是将生成好的静态文件放在github上,没有源码。如果在另一台设备就没法。
思路:在原有仓库建一个分支,源码的拉取和推送都在分支上。但是hexo g && hexo d会弄到主干上
实现
创建分支(在 Github上操作)
首先在Github上面创建一个分支命名为hexo,hexo 是从master 拉取,所以分支的文件和 master 一样。
初始化分支(PC1上面操作)
在已经部署好Hexo环境的PC1上的安装Hexo的根目录下拉取 hexo 分支,步骤如下:
git clone 仓库地址将仓库文件拉取到本地,生成的文件名为 username.github.io;进入username.github.io文件夹,除了 .git 文件夹以外,其他文件全部删除;
git add .将修改提交至暂存区;
git commit -m “提交说明”提交本次修改;
git push origin Hexo将本次修改推送到远端 Hexo;将刚才未删除的 .git 文件夹拷贝至Hexo根目录,删除 username.github.io 文件夹,此时本地的Hexo目录已与 Github上面的 Hexo 文件夹关联了,而且默认的 .gitignore 已经配置了忽略规则,所以已经可以将根目录下的文件同步上去,还是依次调用 git add . 、git commit -m ‘comment’、 git push origin Hexo 三个命令将当前的文件推送至远程的 Hexo分支。
同步分支(PC2上面操作)
此时在PC2上,创建文件夹Blog,在Blog文件夹下面还行以下操作:
git clone 仓库地址 BlogName
git clone -b hexo 仓库地址 hexo.repo //这一步是将Hexo分支的代码拉到hexo.repo里面。名字可以自己起。在clone下来的仓库文件夹中将hexo.repo 文件夹下的文件拷贝到 BlogName 目录中(这里把hexo.repo里面的所有文件夹包括.git一起拷贝过去,这时候本地的分支就是Hexo。虽然远程和本地都有Hexo,但是PC2没有master。那么以后的推送或拉取都要把分支指定完全 git push origin Hexo:Hexo git pull origin Hexo:Hexo)
其实上面的问题,在pc2上把hexo.repo的文件复制过去后,可以再建一个master,把远程仓库的master拉到本地master应该就可以了,虽然这个办法没尝试过,但是下次可以试试。
然后安装和配置hexo环境,依次调用命令: npm install hexo、npm install、npm install hexo-deployer-git;(不需要hexo init)此时通过命令 hexo g、hexo s即可在本地开启同步下来的博客静态页面,并通过 http://localhost:4000/ 访问。
在新设备上使用可能遇到的问题
npm安装好hexo后,把github上的代码拉下来,进入指定目录后,无法使用hexo命令。
原因:缺少node_modules包
可以使用npm install安装,如果不行的话,可以把其他设备的node_modules包拷贝过来新设备hexo g 与 hexo s后,页面是空白的
原因:themes下面的主题文件夹内容为空
可能是当时主题文件夹里面有git文件夹,导致没有上传到github,所以新设备拉去的时候,里面的内容是空的。只需要把原来设备的主题拷贝过来就好
发布博文(PC1或者PC2)
后续不管是PC1还是PC2,如果修改了主题或者新增了博文,按照以下步骤即可:
git add .
git commit -m “修改说明”
git push origin Hexo
hexo g -d博客无法渲染出数学公式
原因
Hexo默认使用”hexo-renderer-marked”引擎渲染网页,该引擎会把一些特殊的markdown符号转换为相应的html标签,比如在markdown语法中,下划线’_’代表斜体,会被渲染引擎处理为标签。
因为类Latex格式书写的数学公式下划线 ‘_’ 表示下标,有特殊的含义,如果被强制转换为标签,那么MathJax引擎在渲染数学公式的时候就会出错。例如,
类似的语义冲突的符号还包括’*’, ‘{‘, ‘}’, ‘\’等。
解决办法:
- 安装Mathjax
MathJax就是我们用来渲染数学公式的js引擎。
不过在这之前,我们还需要卸载自带的hexo-math以避免冲突。
npm uninstall hexo-math --save
npm install hexo-renderer-mathjax --save(npm 后面添加—save,会把包安装到当前的node_modules文件夹下面,如果没有这个,估计是npm的安装位置下的某个位置,和环境变量有异曲同工的意思)
- 更新MathJax的CDN链接
搜索mathjax.html文件,将最后一行cdn地址改为(版本可以根据实际情况修改,我是2.7.3)
<script src="//cdn.bootcss.com/mathjax/2.7.3/MathJax.js?config=TeX-MML-AM_CHTML"></script>- 更换默认渲染引擎
npm uninstall hexo-renderer-marked --save
npm install hexo-renderer-kramed --save- 更改转义规则
首先, 打开/node_modules/kramed/lib/rules/inline.js
第11行的escape变量的值做相应的修改:
escape: /^\\([`*\[\]()#$+\-.!_>])/这一步是在原基础上取消了对\,{,}的转义(escape)。
同时把第20行的em变量也要做相应的修改
em: /^\*((?:\*\*|[\s\S])+?)\*(?!\*)/同时开启mathjax
进入到主题目录,找到_config.yml配置问题,把mathjax默认的false修改为true,具体如下
# Math Formulas Render Support
math:
enable: true
# Default (true) will load mathjax / katex script on demand.
# That is it only render those page which has `mathjax: true` in Front-matter.
# If you set it to false, it will load mathjax / katex srcipt EVERY PAGE.
per_page: true
# hexo-renderer-pandoc (or hexo-renderer-kramed) required for full MathJax support.
mathjax:
enable: true
# See: https://mhchem.github.io/MathJax-mhchem/
mhchem: false每篇文章的开头打开mathjax开关:
title: index.html
date: 2016-12-28 21:01:30
tags:
mathjax: true到这里一般就可以了,要记得hexo clean, 再hexo g,然后hexo s。不要直接hexo s或者hexo server。
- 使用hexo-filter-mathjax
对部分支持MathJax的主题来说,只需在主题配置文件将相关配置项开启即可使用MathJax。但对很多主题,如我使用的CleanBlog主题来说,没有这样的功能。有一个工具可以帮助我们:hexo-filter-mathjax。
npm install hexo-filter-mathjax --savehexo无缘无故出现404
访问的时候突然出现404。hexo clean ,hexo g , hexo d不行; hexo s也不行
访问url是404,hexo s出现的是cannot GET
解决方法
还一个可能产生404的原因便是因为缺少了index.html文件,解决方案如下:
在git bash中敲入
npm install hexo-generator-index --save
之后便有index.html文件了。不妨重新hexo clean,hexo g -d试试。
第一次写博客,还有些生涩,希望可以帮到大家。有问题可直接评论,我会不定期登录博客,和大家一起探讨。
hexo d 发布的时候无法访问到仓库
有时候会遇到这个错:ssh: connect to host github.com port 22: Connection timed out
如果把clash打开/关闭后还是没用,可以这样操作:
找到 ~/.ssh/config 文件(windows是在C/用户/用户名/.ssh/config)
然后添加:
Host github.com
Hostname ssh.github.com
Port 443宽带、带宽、流量
基本概念
- 宽带:通常别人会说你家能不能上网呀?其实这个意思就是你家有没有宽带,换句话说,就是一个名词,先有了宽带一词,然后才可以说你带宽是多少,宽带与上网的速度快慢没有直接关系。
- 带宽:带宽是量词,指的是网速的大小,比如1Mbps的意思是一兆比特每秒
下载速度
如果申请的带宽是10Mb/s这个单位中的b是小写的,而我们刚才说的1B(字节)=8b(位),这里刚好是8倍的关系,即下载速度:10Mb / 8 = 1.25MB
有的人就会问,为什么要除以8?
- 在计算机中,下载速度是以字节(B)为单位的,而提供商说的是以比特(b)为单位的。
流量
流量是对外发送数据与接收数据包的大小总和,单位是采取1024进制的,单位有 B,KB,MB(M),GB(G)
1G=1024MB
1M=1024KB
1KB=1024字节(B)一般我们手机有 5元30MB,10元70MB的流量套餐,当我们打开一个网页,需要多少流量呢?(2005)
假设某一个网页上有 100个汉字与一张100KB的图片,一个汉字=2个字节
即这个页面的数据大小为:100 * 2B / 1024 + 100KB = 0.2KB +100KB =100.2KB;
每访问一次这个页面,将产生100.2KB的流量,如果是70MB的流量,那么访问几个网页基本没有了,所以更不要说看视频了。带宽、网速、流量的关系
1.带宽单位是:比特/秒(bps):10M=10Mbps
2.网速是数据传输的速度,单位是:字节/秒 (B/s, KB/s, MB/s)
1MB/s=1024KB/s
1KB/s=1024B/s3.流量是用户上网 发送和接收 的 数据量总和 ,单位是:字节(Byte);
比特是信息的最小单位:1字节=8比特 也就是1B=8bit 或者 1B=8b
1字节/秒=8比特/秒 (1B/s=8bps)
1比特 (1b or 1位) 是信息技术中的最小存储单位,1位代表一个“1”或者“0”;
1B(1字节)是比较小的存储单位:一般情况下1个英文字母占1个字节;一个汉字占2个字节;4.他们之间的换算:带宽大小 / 8
传统下载、BT下载,磁链下载
传统下载
采用的是C/S模式,所有的用户都从指定服务器上拿东西,对服务器有较高的要求。如果请求量过大,容易崩
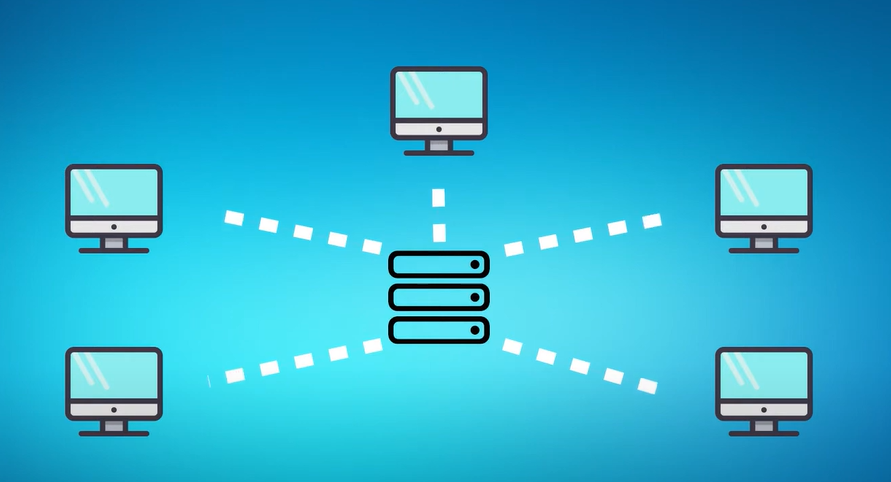
BT下载
简介
BitTorrent(简称BT)是一个文件分发协议,每个下载者在下载的同时不断向其他下载者上传已下载的数据。而在FTP,HTTP协议中,每个下载者在下载自己所需文件的同时,各个下载者之间没有交互。当非常多的用户同时访问和下载服务器上的文件时,由于FTP服务器处理能力和带宽的限制,下载速度会急剧下降,有的用户可能访问不了服务器。BT协议与FTP协议不同,特点是下载的人越多,下载速度越快,原因在于每个下载者将已下载的数据提供给其他下载者下载,充分利用了用户的上载带宽。通过一定的策略保证上传速度越快,下载速度也越快。在很短时间内,BitTorrent协议成为一种新的变革技术。
BitTorrent 的发展依赖于peer-to-peer技术,在P2P网络中,每个参与的节点既是服务器又是客户端,既是信息的提供者又是信息的消费者。
为什么说下载的人越多,下载速度越快?
假如目标文件目前有4个人持有,那我从4个人手里面取走一部分,拼凑起来就可以获得目标文件,但是理论用时为原来的1/4。
大概流程
种子会告诉我联系哪个追踪服务器,然后服务器告诉我该找谁要资源。
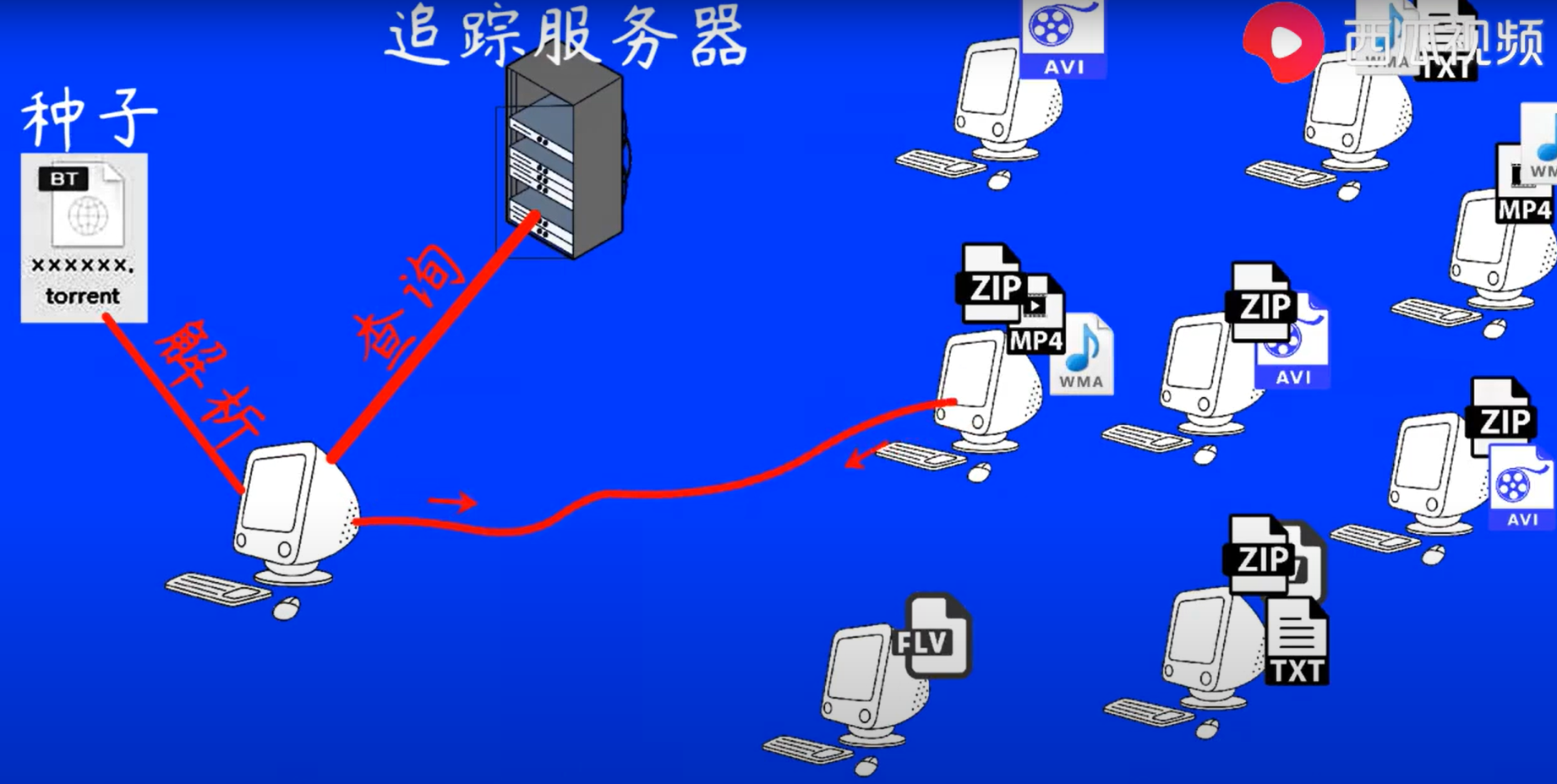
但是这种方式存在一个弊端,没有存在真正的去中心化,如果tracker被干掉了,那么种子就会失效。(因为大量网民下载盗版的,有电源公司和唱片公司等会想办法干掉tracker)
磁链接下载
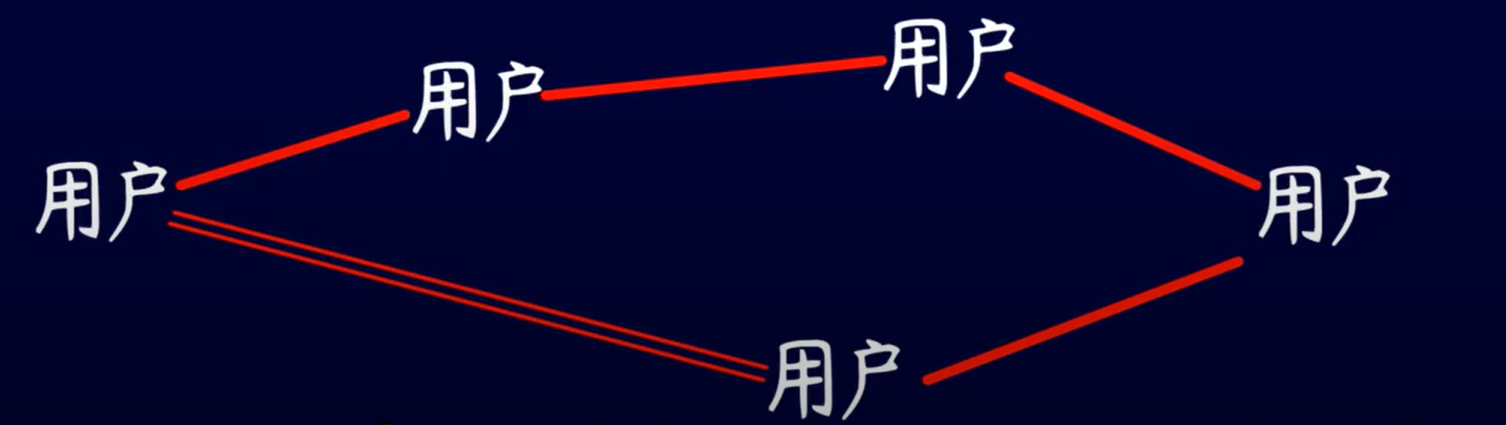
没有种子,没有固定的追踪服务器
追踪服务器都是临时工,由某一个下载者兼任。要找到这个下载者需要多方打听。看看自己名单里面谁和这个下载者最近,然后层层联系。
知识百科
飞机为什么能飞起来
几百吨重的飞机为什么能飞起来? - 无敌铁憨憨的回答 - 知乎
https://www.zhihu.com/question/482015979/answer/3325853989
人们日常被空气所包围,一般情况下感受不到。如果跑得很快就能感受到,如果到音速,会更加明显。
当速度很快时候,你还想继续跑,你就必然要不断去挤开前面的空气…为啥战斗机头是尖的而不是弄个方块儿?就是为了容易挤。
绿色代表原来的空气,往前跑把前方的空气按照黄色轨迹挤压到了两侧。
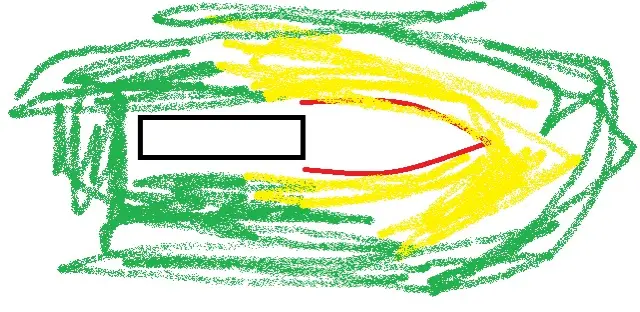
但这样子的话它是飞不起来的。
于是飞机翅膀上会有个能活动的板子,当起飞时候它会向下打开。降落时候会朝上打开…
起飞时候打开,前方被挤开空气的一部分,会被这个板子挡一下,然后导致一个堆叠,例如紫色这部分就代表着因为挡住没有及时流通走而堆叠的空气。
正常情况下,紫色这堆淤积在那儿的空气,肯定是要沿着红色箭头方向散出去的……
然后它往箭头方向去挤压,那其他正常流通的黄色的空气,也会给这堆紫色空气一个反作用力(蓝色箭头),不让紫色那一堆太容易挤进来…

堆积的越来越多,就起飞了…
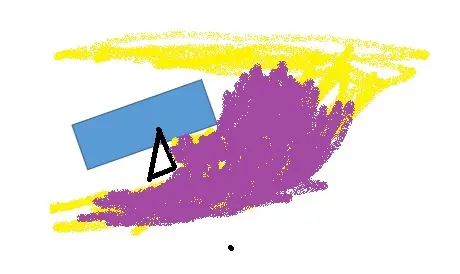
飞机为什么不会掉下来
正常情况下它会受重力影响逐渐下来对吧?
但是本来它上下左右前后都有空气,假设绿色的那些。然后它高速把前方绿色空气挤到两侧,按照黄色线条轨迹…那这堆被从前面挤过来的空气,是要按照黄色箭头继续往上、下侧再挤的……结果原本在上下侧绿色的空气,又不愿意那么轻松就被这些从前面挤过来的气流再插进来,于是会给这些想往上下侧挤进来的气流一个橙黄色的反作用力,如果下侧给的反作用力等于重力,这东西它就会平着飞了。

只要不失速,就基本安全
即便你说遇到很大的气流颠簸,你就理解为前方很多很多空气墙厚度都不一样,所以一个个撞过去然后被挤压到两侧的气流量有不同…
但只要不失速那就可控…
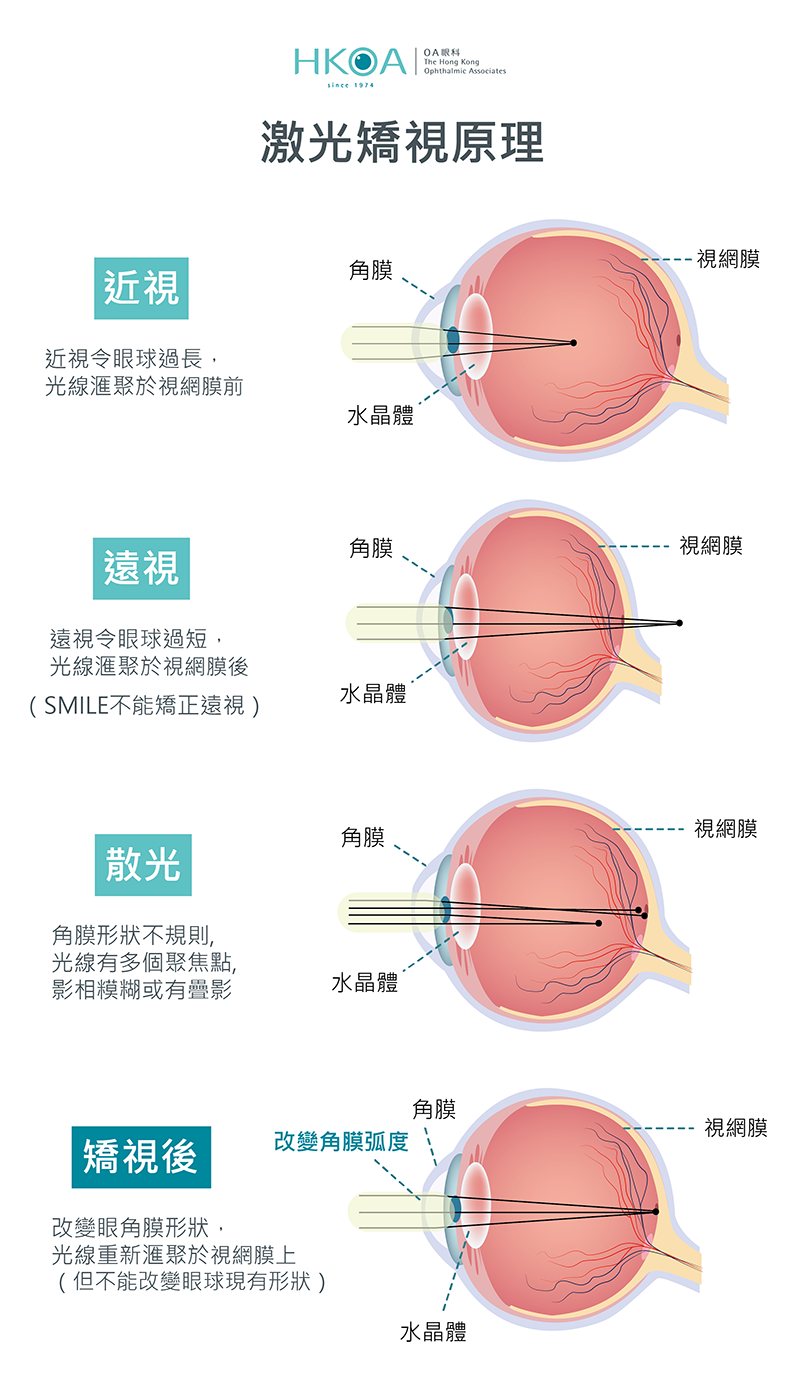
近视和飞秒手术
【你近视散光吗?你了解眼镜吗?】 https://www.bilibili.com/video/BV1qx411k7AH/?share_source=copy_web&vd_source=0aac08942099868c6eaf781c9de8ebb1
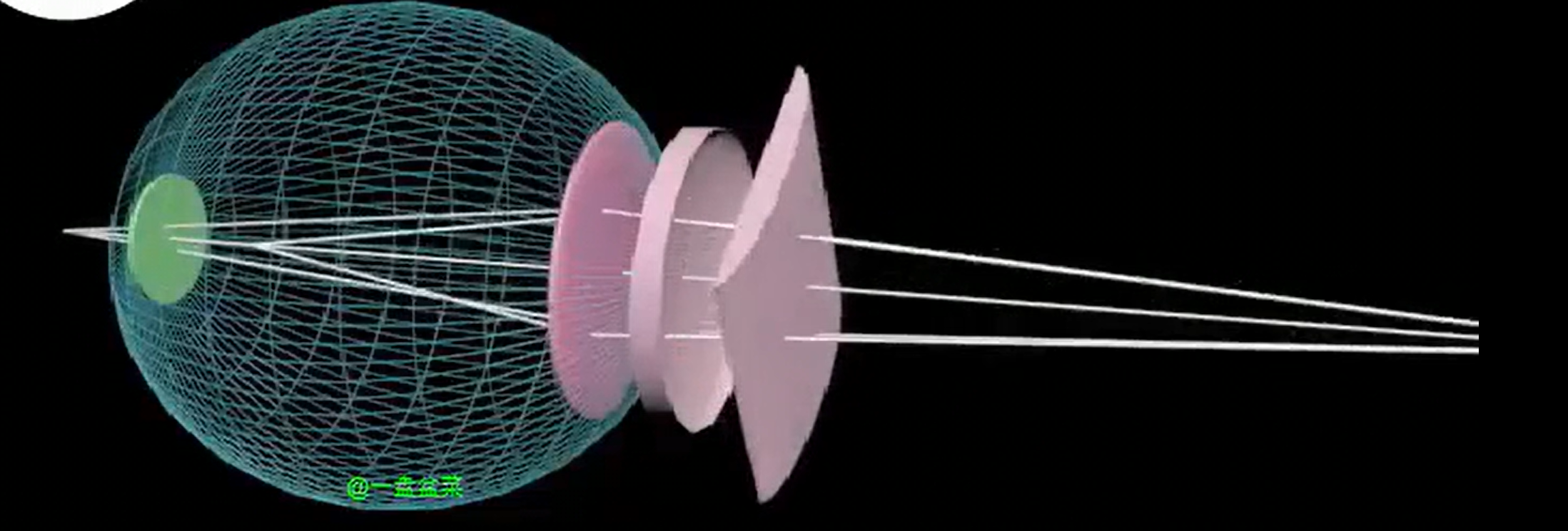
晶状体调节
物体的远近会影响在视网膜上的成像(远近),为了看清楚,晶状体会跟着调节。
更近的物体,成像落在视网膜后方,肌肉压缩晶状体,变凸,成像在视网膜上
更远的物体,成像落在视网膜前方,肌肉放松晶状体,被拉长,成像在视网膜上
近视原因
近视分为两种情况:真性近视和假性近视
假性近视也称为屈光性近视,肌肉长期紧张,晶状体可以变凸,但是没法放松,所以看远的看不清楚。但是眼轴正常
真性近视就是眼轴变长了
长时间静距离用眼,导致眼轴变长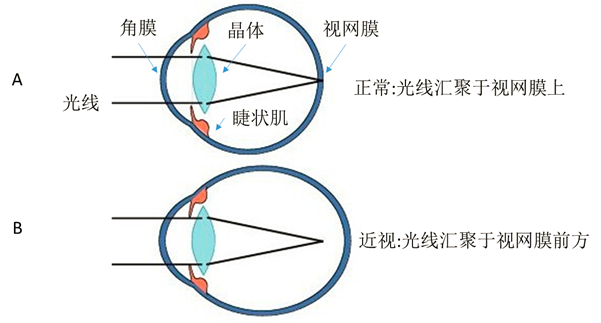
红绿测试
红光波长长,偏转角度小,落在视网膜后方;绿光波长短,偏转角度大,落在视网膜前方
可以想象三节棍,九节鞭和长绳。长绳可以理解为由很多距离小的短连接起来的。
长绳=多节鞭
长绳弯曲是最容易的。所以波长短的偏转角度大
验光的时候红光比绿光清晰是正常的,因为你是近视眼,看不清视网膜前面的光线是正常的。最终需要调节到两个颜色差不多的程度。
散光
眼球变形导致眼角膜被压弯,水平方向的光线会边远,竖直方向的会变近。近视镜片无法把它们聚集在同一点。
散光相当于在眼球前面加了个凸柱镜和凹透镜。眼球变形的方向不同,相当于凸柱镜的轴向不同,也就是散光的轴向
飞秒手术原理
把角膜切一部分,变成一个凹面镜,让光线落到视网膜上。
验光单
近视+散光(眼镜店验光单):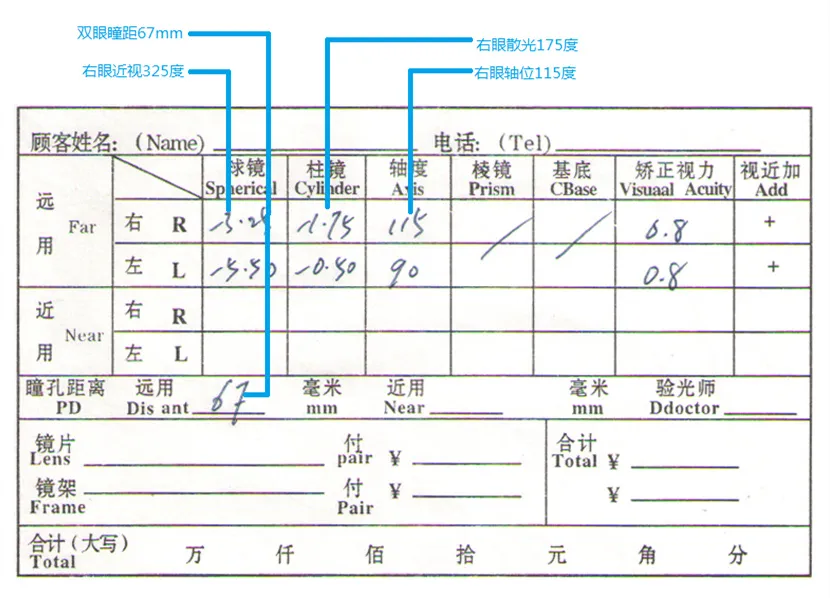
单纯近视(机打验光单):
上面两个图都是近视眼的验光单。如果是远视眼,那么前面不是负号(-),而是加号(+)



