数学知识

凸优化（Convex Optimization）

凸集（Convex Set）

凸集是一系列点的集合，凸集中任意两点之间所连线段一定落在集合内部，如下图所示。

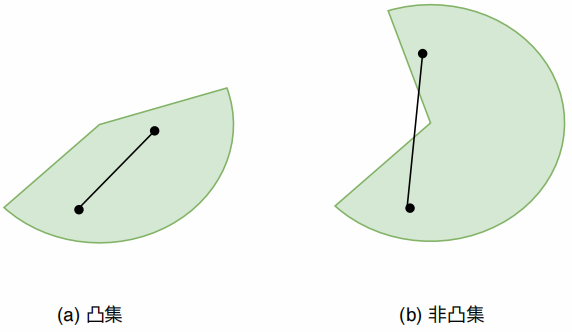
站在集合内部看向集合边界时，集合的边界都是向外凸出的，就是凸集；如果是向内凹陷的，就不是凸集。

凸集的定义

空间，对于某个子集，从中挑选任意两个元素，对于，如果满足：

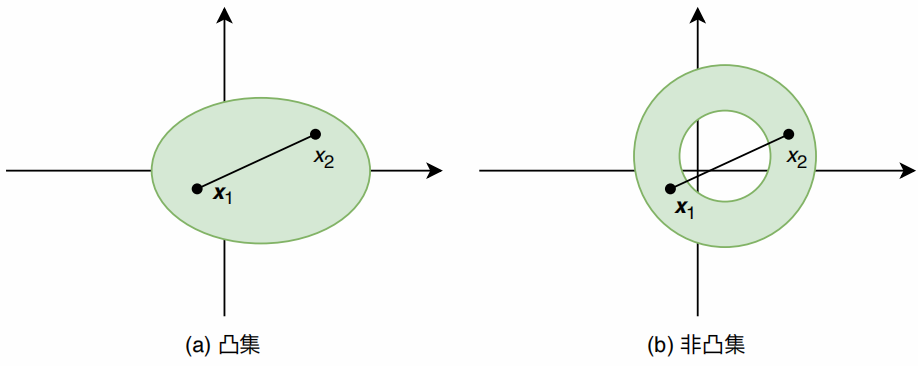
那么集合S是一个凸集，否则为非凸集。该判断标注和凸集的定义是定价的，本质是看元素之间所连线段是否落在集合内部，如下图所示：

凸函数

基于凸集的概念可以定义凸函数。凸函数一类具有特殊性质的函数统称，如果函数的定义域为凸集，且对于定义域内任意两个元素，对任意满足：

即函数上任意两点所连线段落于函数曲线上方或恰好在曲线上，称为凸函数，否则为非凸函数。下图展示时的情况：

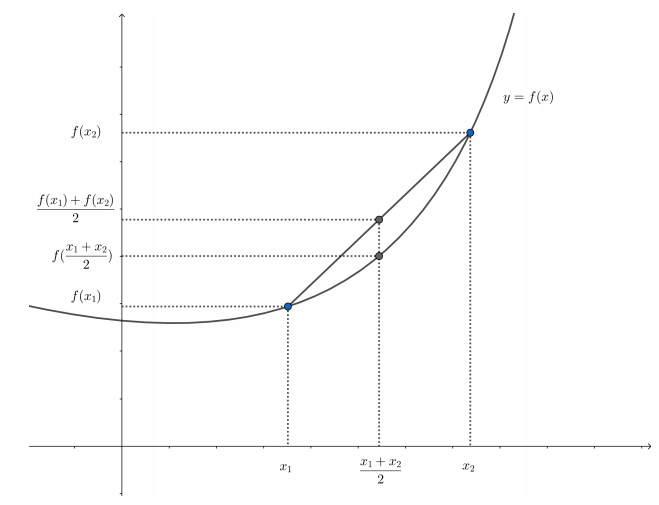
如果是凸函数，则称为凹函数（Concave Function）。凸函数或凹函数并不是两者必取其一，如果的函数形状存在起伏或没有规律，既不是凸函数也不是凹函数。

函数最小值

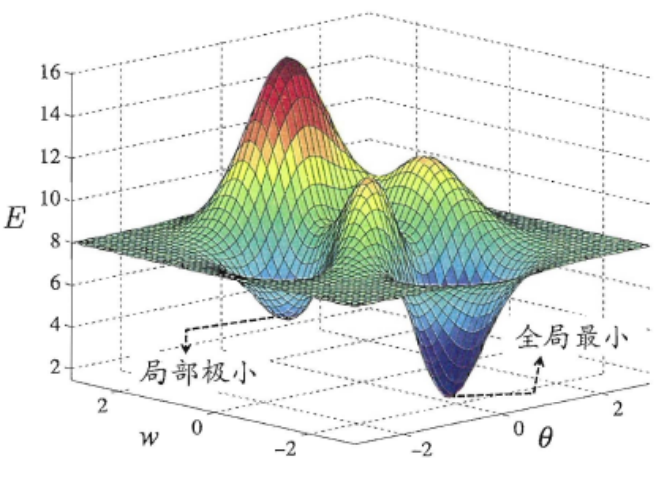
对任意一个函数，可能存在多个局部极小点，但全局最小点只有一个。但如果是凸函数，那么只存在一个局部极小点，该点也就是非全局最小点。

求解函数最小值的常用方法就是梯度下降法。深度学习中的损失函数通常是非凸函数，只能得到局部极小点。非凸问题的传统做法：

• 块坐标下降法：每次迭代的过程中，只针对一个变量进行优化求解，其余变量保持不变，然后交替求解。
• 逐次凸逼近法：将目标函数在定点进行一阶泰勒展开，然后构建近似函数，近似函数代替原目标函数进行求解。
• 松弛变量引入法：引入松弛变量，将原目标函数中难以解决的公式部分用松弛变量代替，使目标函数变为凸函数。

k-means相关

k-means

k-means也被称为k均值算法，算法运行流程：
运行流程：

• 1.初始化质心：随机选择 K 个样本作为初始质心。
• 2.分配样本：将每个样本分配到最近的质心（基于距离，如欧氏距离）。
• 3.更新质心：重新计算每个簇的质心（所有样本的均值）。
• 4.迭代收敛：重复步骤 2-3，直到质心不再变化或达到最大迭代次数。

其中的优化函数或优化目标定义如下：

给定样本集，划分簇

每个簇内的均值向量

注意：表示的是簇里面的包含的数据个数，就是里面有多少个，而不是这个簇里面的数据点模。

而K-means的目标是最小化每个聚类的平方误差之和。

值越小则簇内样本相似度越高。