深度学习

卷积相关的内容

网络模型参数的关系

编码器：

convlstm_encoder_params = [
    [
        OrderedDict({'conv1_leaky_1': [1, 16, 3, 1, 1]}),
        OrderedDict({'conv2_leaky_1': [64, 64, 3, 2, 1]}),
        OrderedDict({'conv3_leaky_1': [96, 96, 3, 2, 1]}),
    ],

    [
        CLSTM_cell(shape=(64,64), input_channels=16, filter_size=5, num_features=64),
        CLSTM_cell(shape=(32,32), input_channels=64, filter_size=5, num_features=96),
        CLSTM_cell(shape=(16,16), input_channels=96, filter_size=5, num_features=96)
    ]
]

OrderedDict定义了一个卷积层的参数，包括输入通道数、输出通道数、卷积核大小、步长和填充。

CLSTM_cell定义了一个CLSTM单元，包括特定的形状、输入通道数、滤波器（卷积核）大小和特征数量（隐藏状态通道数）。

下面给一个具体的例子：
输入到编码器的特征维度为（16, 10, 1, 64, 64）。

经过第一个卷积层conv1_leaky_1后，输出特征维度变为（16, 10, 16, 64, 64）。

之后，这个输出进入到第一个CLSTM_cell，此时shape为（64, 64），输入通道为16，经过卷积LSTM后，输出特征维度为（16, 10, 64, 64, 64）。

然后，这个输出经过第二个卷积层conv2_leaky_1，输出特征维度变为（16, 10, 64, 32, 32）。

然后，这个输出进入到第二个CLSTM_cell，此时shape为（32, 32），输入通道为64，经过卷积LSTM后，输出特征维度为（16, 10, 96, 32, 32）。

然后，这个输出经过第三个卷积层conv3_leaky_1，输出特征维度变为（16, 10, 96, 16, 16）。

最后，这个输出进入到第三个CLSTM_cell，此时shape为（16, 16），输入通道为96，经过卷积LSTM后，输出特征维度为（16, 10, 96, 16, 16）。

此时已经完成了编码阶段，这个输出将作为解码器的输入。

在解码阶段，过程类似：

这个输出经过第一个反卷积层deconv1_leaky_1，输出特征维度变为（16, 10, 96, 32, 32）。

然后，这个输出进入到第一个解码器的CLSTM_cell，此时shape为（32, 32），输入通道为96，经过卷积LSTM后，输出特征维度为（16, 10, 96, 32, 32）。

然后，这个输出经过第二个反卷积层deconv2_leaky_1，输出特征维度变为（16, 10, 96, 64, 64）。

然后，这个输出进入到第二个解码器的CLSTM_cell，此时shape为（64, 64），输入通道为96，经过卷积LSTM后，输出特征维度为（16, 10, 64, 64, 64）。

最后，这个输出经过最后一个卷积层conv3_leaky_1和conv4_leaky_1，最后的输出特征维度为（16, 10, 1, 64, 64），这就是最后的输出结果。

图像尺寸、卷积核大小、步长、填充之间的关系或数学公式

输出高度 = (输入高度 - 核高度 + 2 * 填充) / 步长 + 1
输出宽度 = (输入宽度 - 核宽度 + 2 * 填充) / 步长 + 1

反卷积层：图像尺寸、卷积核大小、步长、填充之间的关系或数学公式

OutputSize = (InputSize - 1) * Stride - 2 * Padding + KernelSize + OutputPadding

其中：

InputSize 是输入特征图的尺寸。
Stride 是卷积核移动的步长。
Padding 是在输入特征图周围填充的零的数量。
KernelSize 是卷积核的尺寸。
OutputPadding 是添加到输出尺寸的额外元素数量。一般在进行转置卷积时，如果希望输出尺寸刚好是输入尺寸的某个倍数，且不能通过调整步长和填充来达到，那么就需要使用OutputPadding。
例如，如果你的输入特征图尺寸为16x16，你希望将其上采样为32x32，你使用的卷积核大小为4，步长为2，那么你可以将填充设置为1，无需OutputPadding。此时，使用上述公式计算得到的输出尺寸就为：

OutputSize = (16 - 1) * 2 - 2 * 1 + 4 + 0 = 32

因此，你的输出特征图的尺寸就为32x32。

卷积神经网络（CNN）

传统神经网络

原文链接

神经网络搭建需要满足三个条件：

1. 输入和输出
2. 权重（w）和阈值（b）
3. 多层感知器的结构

其中，最困难的部分就是确定权重（w）和阈值（b）。目前为止，这两个值都是主观给出的，但现实中很难估计它们的值，必需有一种方法，可以找出答案。

这种方法就是试错法。其他参数都不变，w（或b）的微小变动，记作Δw（或Δb），然后观察输出有什么变化。不断重复这个过程，直至得到对应最精确输出的那组w和b，就是我们要的值。这个过程称为模型的训练。

因此，神经网络的运作过程如下：

1. 确定输入和输出
2. 找到一种或多种算法（数学公式），可以从输入得到输出
3. 找到一组已知答案的数据集，用来训练模型，估算w和b
4. 一旦新的数据产生，输入模型，就可以得到结果，同时对w和b进行校正

传统神经网络数学公式推导（全连接）

原文链接

传统神经网络的问题

1. 图像需要处理的数据量太大，导致成本很高，效率很低

现在随随便便一张图片都是 1000×1000 像素以上的， 每个像素都有RGB 3个参数来表示颜色信息。

假如我们处理一张 1000×1000 像素的图片，我们就需要处理3百万个参数！

1000×1000×3=3,000,000

卷积神经网络 – CNN 解决的第一个问题就是「将复杂问题简化」，把大量参数降维成少量参数，再做处理。

1. 图像在数字化的过程中很难保留原有的特征，导致图像处理的准确率不高
   

假如有圆形是1，没有圆形是0，那么圆形的位置不同就会产生完全不同的数据表达。但是从视觉的角度来看，图像的内容（本质）并没有发生变化，只是位置发生了变化。

所以当我们移动图像中的物体，用传统的方式的得出来的参数会差异很大！这是不符合图像处理的要求的。

CNN 解决了这个问题，他用类似视觉的方式保留了图像的特征，当图像做翻转，旋转或者变换位置时，它也能有效的识别出来是类似的图像。

具体表现为：

CNN（卷积神经网络）相对于传统的全连接神经网络（FNN），可以通过卷积层（权值共享、局部连接）和池化层（空间维度的降采样）的设计来实现参数降维，从而减少模型中的参数数量。

CNN的基本步骤

卷积神经网络（Convolutional Neural Network，CNN）是一种在计算机视觉和图像处理任务中广泛应用的深度学习模型。CNN通过模拟生物视觉系统中神经元的工作原理，能够自动学习图像和视频等数据的特征表示。

CNN的基本概念包括以下几个要素：
相关链接，写的不错

1. 卷积层（Convolutional Layer）：卷积层是CNN的核心组成部分。它通过使用一系列可学习的滤波器（也称为卷积核）对输入图像进行卷积操作，从而提取图像中的局部特征。卷积层的输出被称为特征图（Feature Map）。

2. 池化层（Pooling Layer）：池化层用于减少特征图的空间维度，同时保留主要的特征信息。池化层也称为下采样。常用的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。池化层可以帮助减少计算量，提取图像的不变性，并且能够控制模型的过拟合。

3. 激活函数（Activation Function）：激活函数引入非线性性质，使得CNN能够学习复杂的非线性特征。常用的激活函数包括ReLU（Rectified Linear Unit）、Sigmoid和Tanh等。

4. 全连接层（Fully Connected Layer）：全连接层将前面的卷积层和池化层的输出连接到输出层，进行最终的分类或回归任务。

5. 反向传播（Backpropagation）：CNN利用反向传播算法进行训练。反向传播通过计算损失函数关于模型参数的梯度，以更新模型参数来最小化损失函数。

下面是一个简单的CNN示例，以图像分类为任务：

输入：一张32x32像素的彩色图像

1. 卷积层：使用一组3x3大小的卷积核，对输入图像进行卷积操作，得到特征图。
2. 激活函数：对特征图的每个元素应用ReLU激活函数，增加非线性性质。
3. 池化层：使用2x2大小的最大池化，将特征图的尺寸减半。
4. 卷积层：再次使用一组3x3大小的卷积核，对池化后的特征图进行卷积操作，得到新的特征图。
5. 激活函数：对新的特征图的每个元素应用ReLU激活函数。
6. 池化层：再次使用2x2大小的最

大池化，将特征图的尺寸减半。

1. 展平层（Flatten）：将池化层的输出展平为一维向量。
2. 全连接层：将展平的向量连接到全连接层，并应用激活函数。
3. 输出层：使用适当的激活函数（如Softmax）进行多类别分类。

这个例子只是一个简化的CNN结构，实际中可能会有更多的卷积层、池化层和全连接层，以及一些正则化和优化技巧，来提高模型的性能和稳定性。

请注意，具体的CNN结构和参数设置会根据不同的任务和数据集而有所不同，需要根据实际情况进行调整和优化。

CNN数学公式推导

链接1

链接2

二维卷积公式：

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

输出图像的高、宽计算公式:

卷积的过程：

卷积神经网络是权值共享，非全连接的神经网络。以2个卷积层和2个池化层的卷积神经网络为例，其结构图如下：

从这个图可以看出几个关键的地方：

1. 卷积层和池化（采样）层结束的时候都需要一个激活函数，就是f(.)。
2. 卷积核可以不止有一个，可以采用多个卷积核分别进行卷积, 这样便可以得到多个特征图。有时, 对于一张三通道彩色图片, 或者如第三层特征图所示, 输入的是一组矩阵, 这时卷积核也不再是一层的, 而要变成相应的深度.

上图中是经过一次卷积后的结果，得到了3个特征图。再次卷积时，输入的是一组矩阵, 这时卷积核也不再是一层的, 而要变成相应的深度。, 最左边是输入的特征图矩阵, 深度为 3, 补零(Zero Padding)层数为 1, 每次滑动的步幅为 2. 中间两列粉色的矩阵分别是两组卷积核, 一组有三个, 三个矩阵分别对应着卷积左侧三个输入矩阵, 每一次滑动卷积会得到三个数, 这三个数的和作为卷积的输出. 最右侧两个绿色的矩阵分别是两组卷积核得到的特征图。

如何理解多尺度CNN中的尺度

在多尺度CNN中，”多尺度”指的是对输入数据进行不同尺度的处理和分析。这种处理方式可以帮助网络更好地捕捉到输入数据中的多尺度特征，从而提高模型的性能和泛化能力。

通常，多尺度CNN会通过以下几种方式来实现多尺度处理：

1. 多尺度输入：将输入数据在不同尺度下进行变换，例如通过缩放、裁剪或填充等操作，以获取不同尺度的图像输入。这样，网络可以同时关注不同尺度下的特征信息。

2. 多尺度卷积：在网络的某些层中使用不同大小的卷积核或不同步长的卷积操作，以捕捉不同尺度的特征。这样，网络可以通过不同尺度的卷积感受野来分析输入数据。

3. 多尺度池化：在池化层中使用不同大小的池化窗口或不同步长的池化操作，以对特征图进行降采样。这样可以保留不同尺度下的特征信息。

4. 多尺度特征融合：将来自不同尺度的特征进行融合，以综合利用不同尺度的信息。这可以通过特征图的级联、加权求和、并行分支等方式来实现。

通过多尺度处理，多尺度CNN能够更好地适应不同尺度的目标或特征，并更全面地理解输入数据。这对于许多计算机视觉任务如目标检测、语义分割和图像分类等是非常有益的。

什么是CNN的尺度(scale)

原文链接

相关链接

卷积神经网络里涉及到三种尺度：深度、宽度、分辨率。

• 深度指的是网络有多深，或者说有多少层。
• 宽度指的是网络有多宽，比如卷积层的通道数。
• 分辨率指的是输入卷积层的图像、特征图的空间分辨率。

也可以简单的理解为不同尺寸的图片，或者不同分辨率的图片。

模型尺度。(a) 是一个基本的网络模型；(b)-(d) 分别单独在宽度、深度、分辨率的维度上增加尺度；(e) 是论文提出的混合尺度变换，用统一固定的比例放缩三个不同维度的尺度。

感受野

若感受野太小，表明网络只能观察到图像的局部特征；若感受野太大，虽然对全局信息理解更强，但通常也包含了许多无效信息。为了提高有效感受野从而避免冗余信息，捕获多尺度特征是当前研究者们常采用的方法。比如拿望远镜看远方为小视野，直接光看为大视野。

循环神经网络（RNN）

总结：

1. RNN这个R(循环)，可以被看做是同一神经网络的多次复制，每个神经网络模块会把消息传递给下一个。
2. 常规的RNN一般是输入和输出是等长序列，为了适应不等长序列。出现了Encoder-Decoder，也叫Seq2Seq。里面的编码器和解码器可以是rnn，也可以是rnn的变种（lstm,gru）等。
3. lstm、gru等都是RNN的变式。主要是为了解决RNN无法处理长序列的缺点。

RNN

人人都能看懂的LSTM - 陈诚的文章 - 知乎

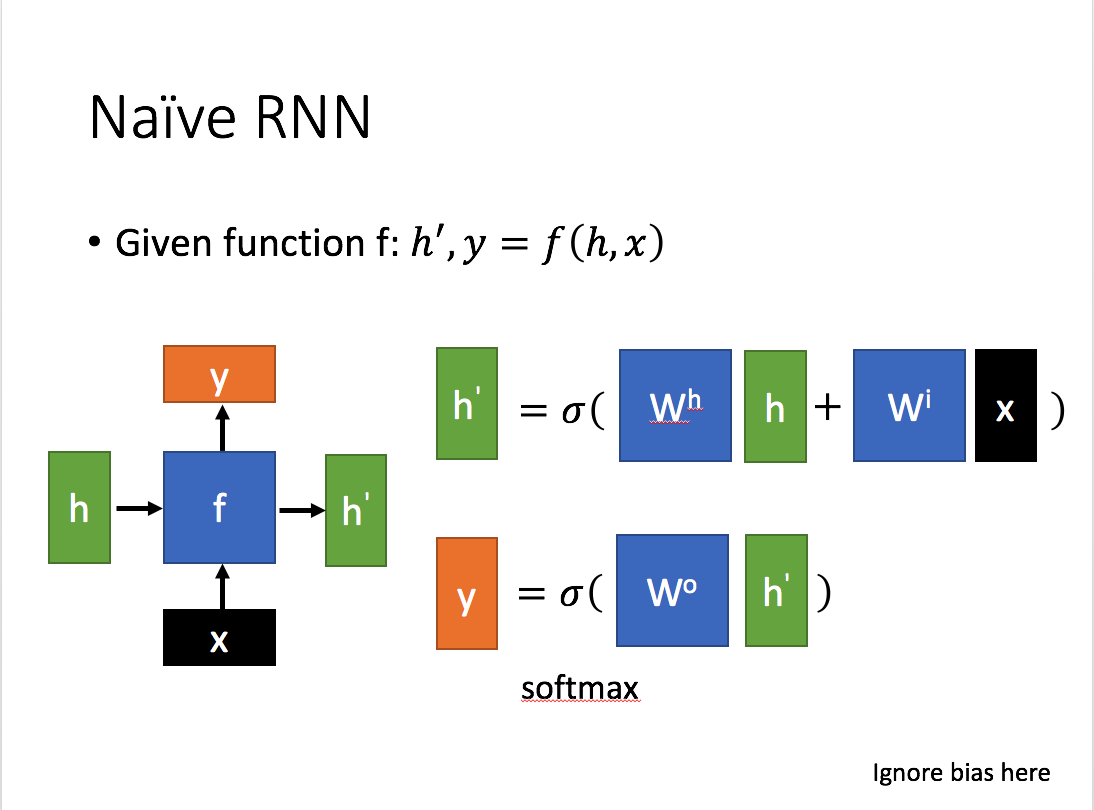
这里：

x为当前状态下数据的输入， h表示接收到的上一个节点的输入。

y为当前节点状态下的输出，而h`为传递到下一个节点的输出。

通过上图的公式可以看到，输出 h’ 与 x 和 h 的值都相关。

而 y 则常常使用 h’ 投入到一个线性层（主要是进行维度映射）然后使用softmax进行分类得到需要的数据。

对这里的y如何通过 h’ 计算得到往往看具体模型的使用方式。

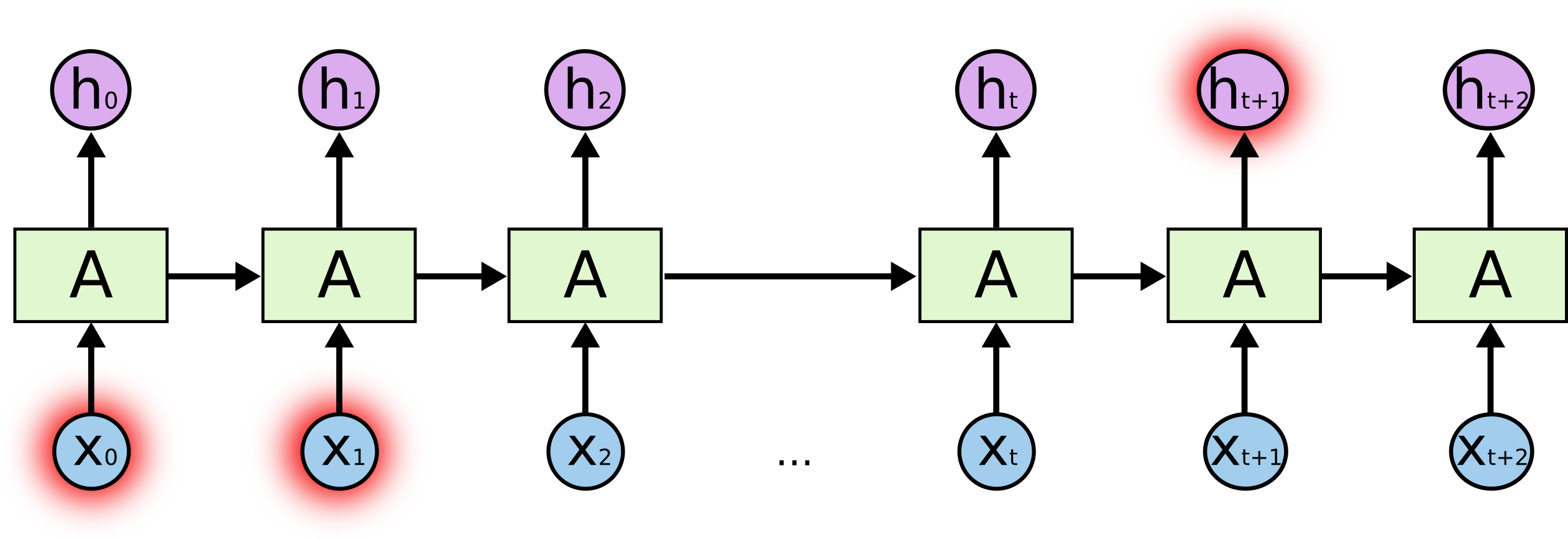
通过序列形式的输入，我们能够得到如下形式的RNN。

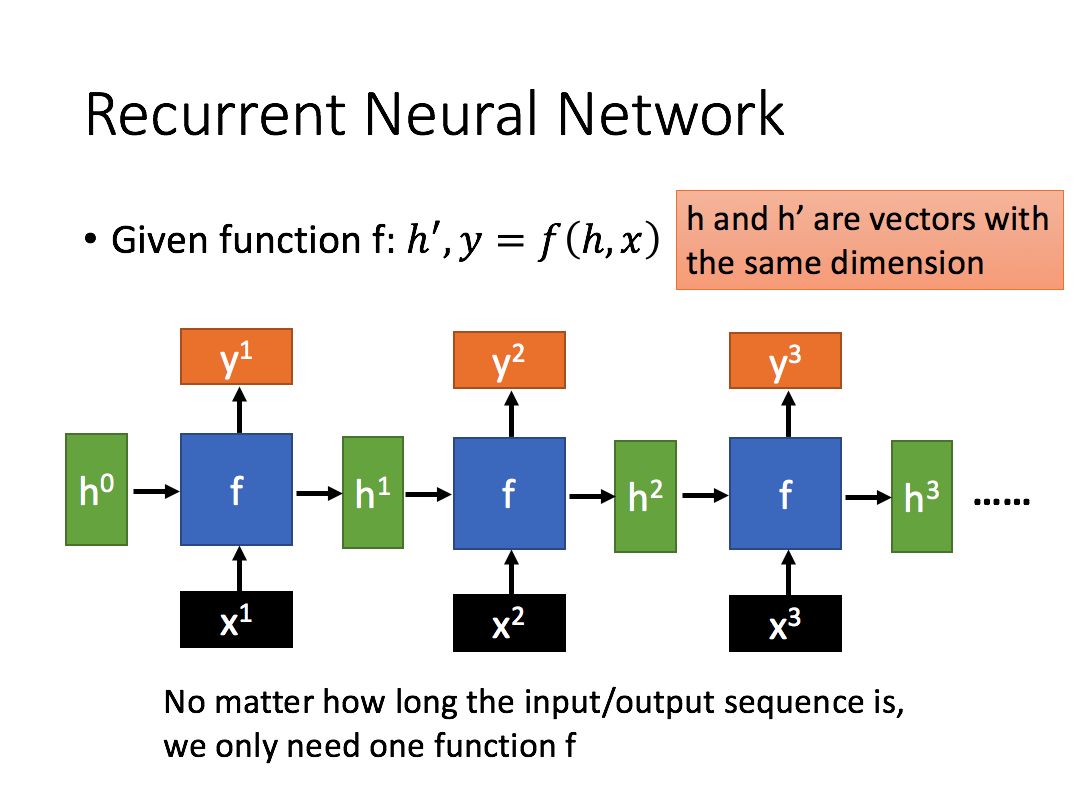
其他rnn图：

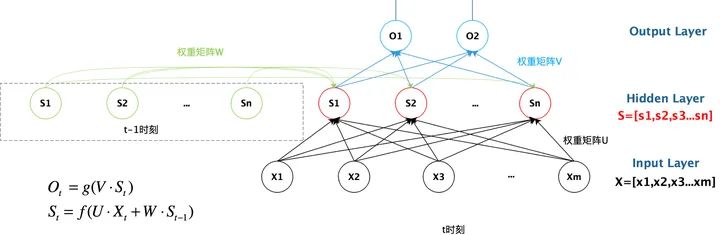
如果我们把上面的图展开，循环神经网络也可以画成下面这个样子：

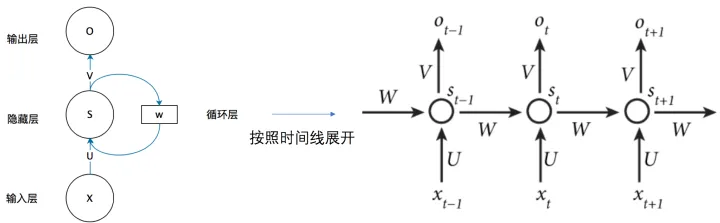
现在看上去就比较清楚了，这个网络在t时刻接收到输入之后，隐藏层的值是，输出值是 。关键一点是,的值不仅仅取决于 ，还取决于 。我们可以用下面的公式来表示循环神经网络的计算方法：

用公式表示如下：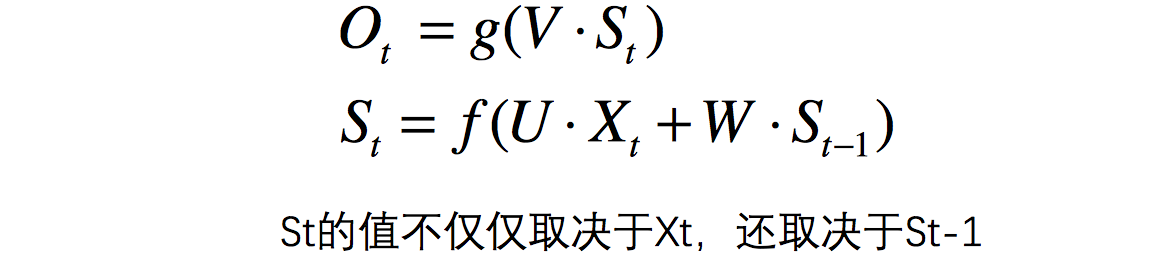

rnn+lstm

rnn

rnn+seq2seq2+attention

RNN的局限：长期依赖（Long-TermDependencies）问题

一些更加复杂的场景。比如我们试着去预测“I grew up in France…I speak fluent French”最后的词“French”。当前的信息建议下一个词可能是一种语言的名字，但是如果我们需要弄清楚是什么语言，我们是需要先前提到的离当前位置很远的“France”的上下文。这说明相关信息和当前预测位置之间的间隔就肯定变得相当的大。

不幸的是，在这个间隔不断增大时，RNN会丧失学习到连接如此远的信息的能力。

在理论上，RNN绝对可以处理这样的长期依赖问题。人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN则没法太好的学习到这些知识。Bengio,etal.(1994)等人对该问题进行了深入的研究，他们发现一些使训练RNN变得非常困难的相当根本的原因。

换句话说， RNN 会受到短时记忆的影响。如果一条序列足够长，那它们将很难将信息从较早的时间步传送到后面的时间步。

因此，如果你正在尝试处理一段文本进行预测，RNN 可能从一开始就会遗漏重要信息。在反向传播期间（反向传播是一个很重要的核心议题，本质是通过不断缩小误差去更新权值，从而不断去修正拟合的函数），RNN 会面临梯度消失的问题。

因为梯度是用于更新神经网络的权重值（新的权值 = 旧权值 - 学习率*梯度），梯度会随着时间的推移不断下降减少，而当梯度值变得非常小时，就不会继续学习。

​

换言之，在递归神经网络中，获得小梯度更新的层会停止学习—— 那些通常是较早的层。 由于这些层不学习，RNN会忘记它在较长序列中以前看到的内容，因此RNN只具有短时记忆。

而梯度爆炸则是因为计算的难度越来越复杂导致。

然而，幸运的是，有个RNN的变体——LSTM，可以在一定程度上解决梯度消失和梯度爆炸这两个问题！

LSTM

总体框架

人人都能看懂的LSTM - 陈诚的文章 - 知乎

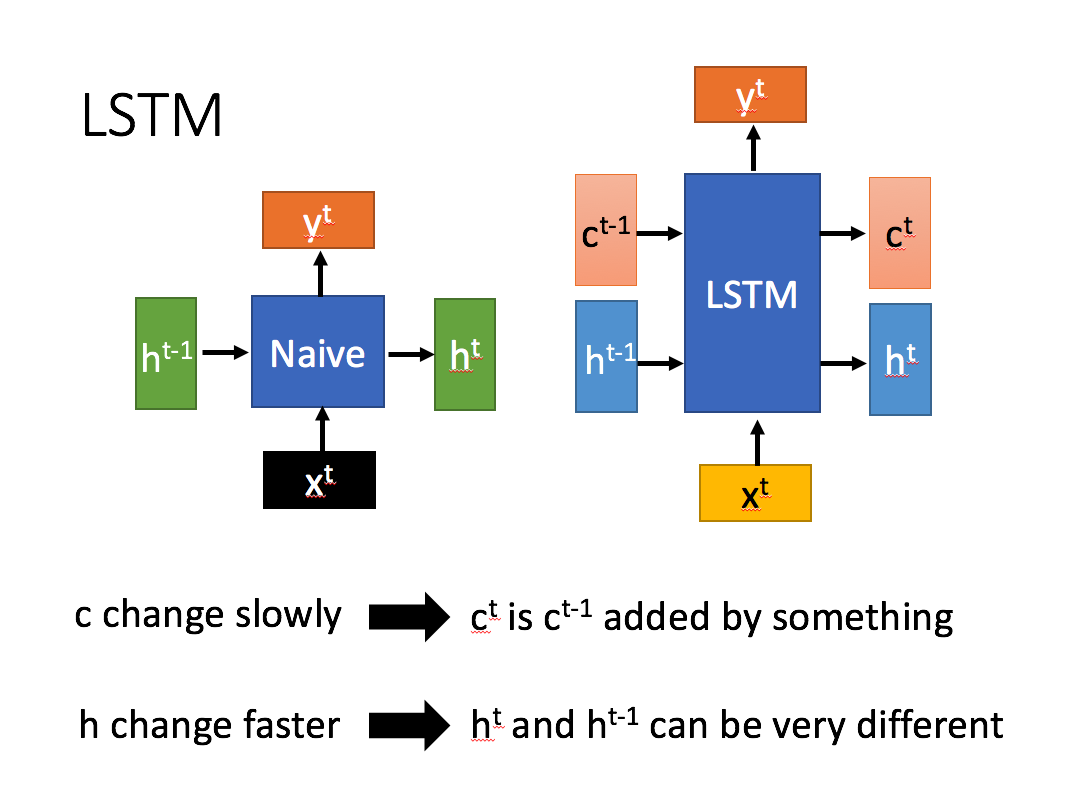
LSTM有两个传输状态，一个（cell state），和一个 （hidden state）

无论是rnn 还是 lstm ,h^t 感觉表示的都是短期记忆，rnn相当于lstm中的最后一个“输出门”的操作，是lstm的一个特例，也就是lstm中的短期记忆知识，而lstm包含了长短期的记忆，其中 C^t就是对前期记忆的不断加工，锤炼和理解，沉淀下来的，而h^t只是对前期知识点的短暂记忆，是会不断消失的。

问题二：C^t 之所以变化慢，主要是对前期记忆和当前输入的线性变换，对前期记忆的更新和变化（可以视为理解或者领悟出来的内容），是线性变换，所以变动不大，而 h^t是做的非线性变化，根据输入节点内容和非线性变化函数的不同，变动固然很大

深入LSTM结构

首先使用LSTM的当前输入和上一个状态传递下来的拼接训练得到四个状态。

:输入门
:忘记门
:输出门

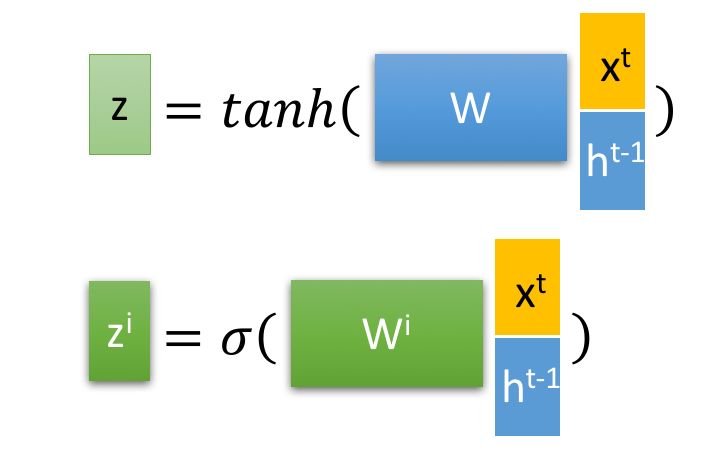
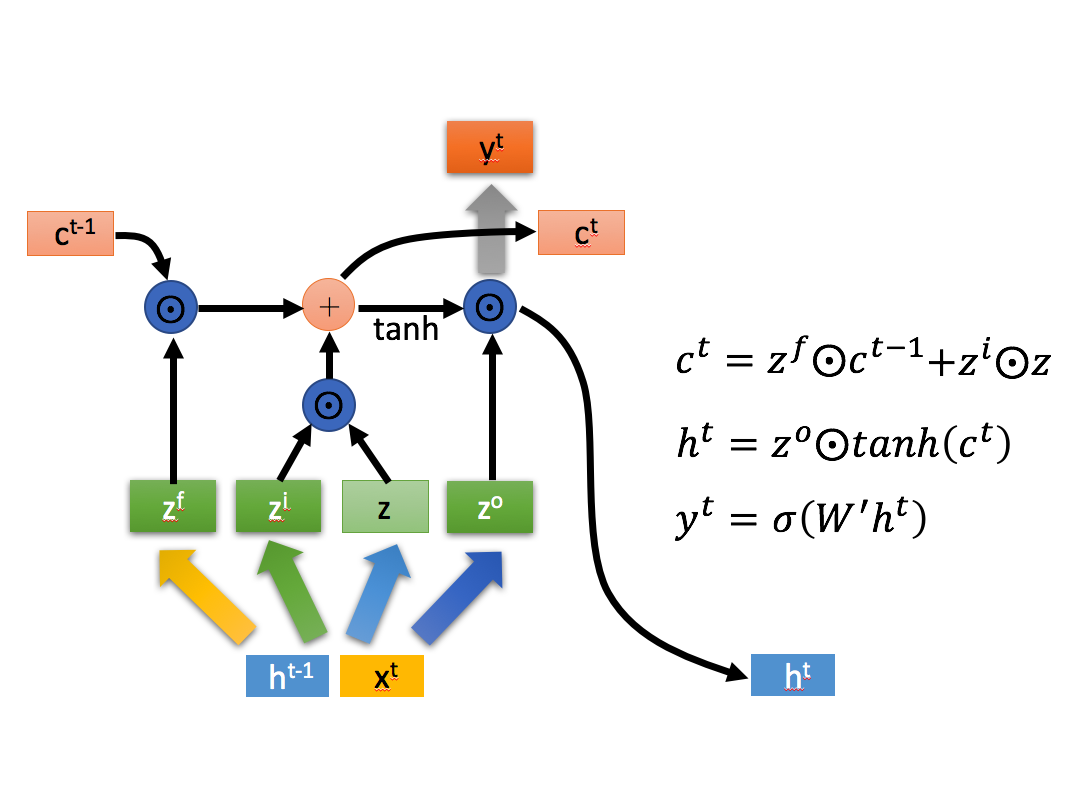
圆圈点代表阵中对应的元素相乘
圆圈加号表示矩阵加法

LSTM内部主要有三个阶段：

1. 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。具体来说是通过计算得到的来作为忘记门控，来控制上一个状态的哪些需要留哪些需要忘。

2. 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的表示。而选择的门控信号则是由
   （i代表information）来进行控制。将上面两步得到的结果相加，即可得到传输给下一个状态的 。也就是上图中的第一个公式。

3. 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 来进行控制的。并且还对上一阶段得到的 进行了放缩（通过一个tanh激活函数进行变化）。

与普通RNN类似，输出往往最终也是通过 变化得到。

LSTM变体

原文链接

Seq2Seq

原文链接

注意力机制

原文

简单理解q,k,v
q:输入搜索引擎中要查询的内容
v:搜索引擎里面有好多文章，每个文章的全文可以被理解成Value
k:文章的关键性信息是标题，可以将标题认为是Key

搜索引擎用Query和那些文章们的标题（Key）进行匹配，看看相似度（计算Attention Score)。我们想得到跟Query相关的知识，于是用这些相似度将检索的文章Value做一个加权和，那么就得到了一个新的信息，新的信息融合了相关性强的文章们，而相关性弱的文章可能被过滤掉。

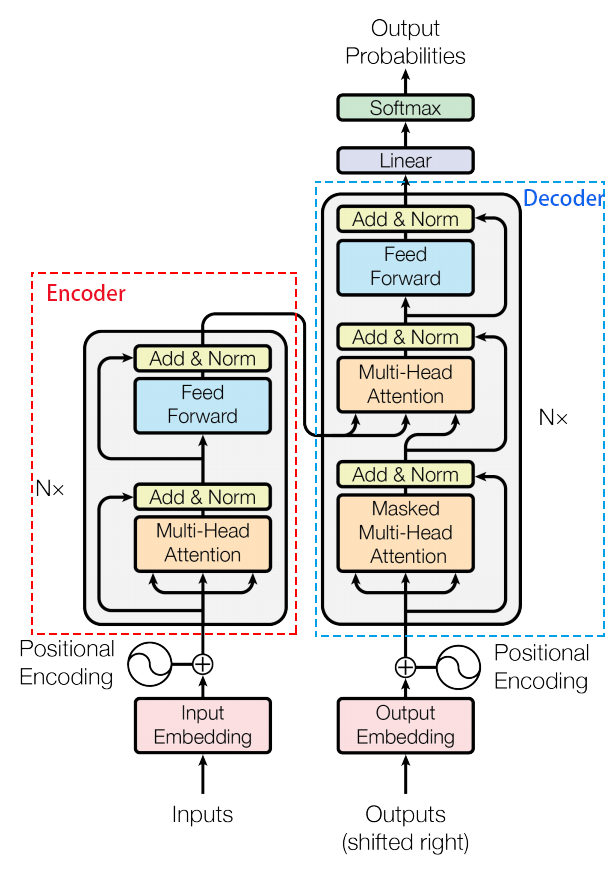
transformer

原文

整体架构：

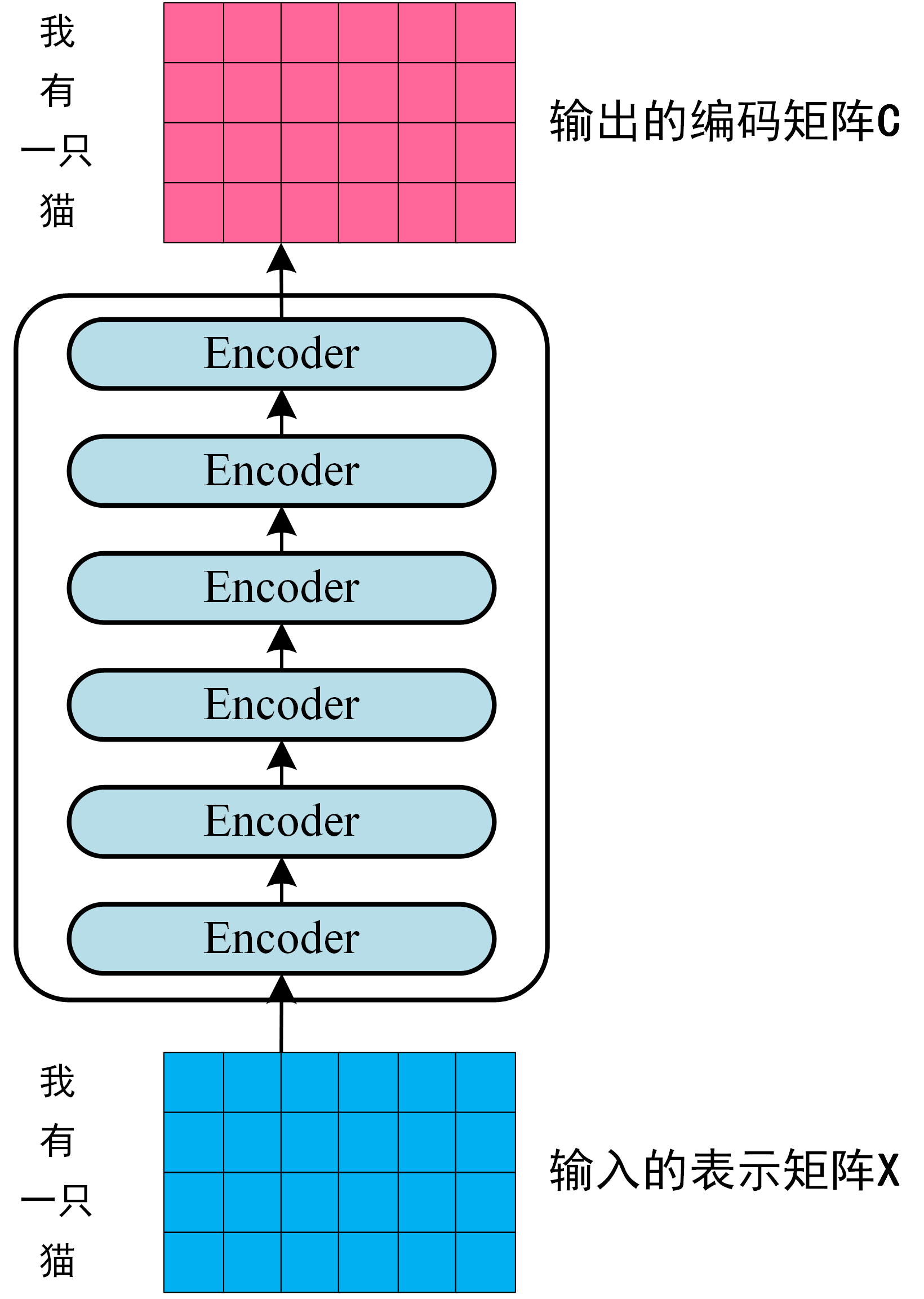
encoder部分

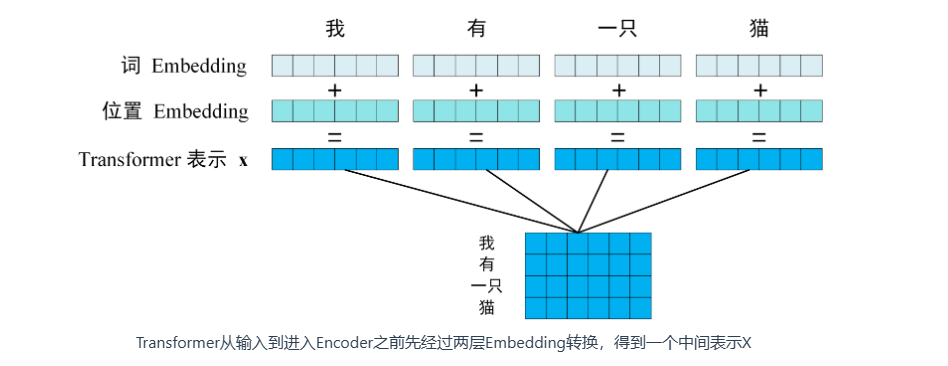
输入形状：（len,d）,len是句子中单词个数，d表示词向量维度。每一个 Encoder Block输出的矩阵维度与输入完全一致。

输入的是图像如何？

对于图像数据来说，第一步必须先将图像数据转换成序列数据，但是怎么做呢？假如我们有一张图片形状为（h,w,c），patch大小为p，那么我们可以创建n个图像patches，可以表示为(n,p,p,c)，其中n = hw/p^2，n就是序列的长度，类似一个句子中单词的个数。在上面的图中，可以看到图片被分为了9个patches。

假设每一个patch是（16,16,3）,铺平后是16163=768；即一个patch变为长度为768的向量，这类似于词向量维度

一般来说，在送入encoder之前，还需要添加位置信息

基于transformer的视频外推和内插

transformer能接受的输入形状是(batch_size, len, d_model)
假如我的任务是视频帧预测，图像原始输入形状是：(batch_size, seq_len, num_channels, width, height)
那么进入模型前，需要转换为：(-1, seq_len, d_model)

外推和内插的一个区别就在于位置编码有些不同。

1. 外推来说，位置编码是为了让模型知道序列中各元素的顺序，关注的是len和d_model，为了和词嵌入匹配；从外推的代码看，特征和标签都是用的同一个位置编码，说明它的作用就是一个位置信息。
2. 内插来说，可以看到，假如位置编码的长度是len，因为输入是一头一尾，所以它们两个的位置编码是：self.positional_encoding[0]和self.positional_encoding[-1]；而中间的插值（预测值）位置编码就是self.positional_encoding[1:-1]

看看代码：

外推：

import torch
import torch.nn as nn

class VideoFramePredictor(nn.Module):
    def __init__(self, num_channels, width, height, seq_len, d_model, nhead, num_encoder_layers, num_decoder_layers):
        super(VideoFramePredictor, self).__init__()

        self.seq_len = seq_len
        self.d_model = d_model

        # 将输入帧转换为模型可以处理的维度
        self.linear_in = nn.Linear(num_channels * width * height, d_model)

        # 位置编码
        self.positional_encoding = nn.Parameter(torch.zeros(seq_len, d_model))
        position = torch.arange(0, seq_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-torch.log(torch.tensor(10000.0)) / d_model))
        self.positional_encoding[:, 0::2] = torch.sin(position * div_term)
        self.positional_encoding[:, 1::2] = torch.cos(position * div_term)

        # Transformer模型
        self.transformer = nn.Transformer(
            d_model=d_model, 
            nhead=nhead, 
            num_encoder_layers=num_encoder_layers,
            num_decoder_layers=num_decoder_layers
        )

        # 将Transformer的输出转换回帧的形状
        self.linear_out = nn.Linear(d_model, num_channels * width * height)

    def forward(self, src, tgt):
        # 将输入和目标帧序列转换为模型可以处理的维度
        src = self.linear_in(src.view(-1, self.seq_len, self.d_model)) + self.positional_encoding
        tgt = self.linear_in(tgt.view(-1, self.seq_len, self.d_model)) + self.positional_encoding

        # 传递给Transformer
        output = self.transformer(src, tgt)

        # 转换回原始帧的形状
        output = self.linear_out(output)
        return output.view(-1, self.seq_len, num_channels, width, height)

# 创建模型实例
num_channels = 1
width = 64  # 假设帧宽度为64
height = 64  # 假设帧高度为64
seq_len = 10
d_model = 512
nhead = 8
num_encoder_layers = 3
num_decoder_layers = 3

model = VideoFramePredictor(num_channels, width, height, seq_len, d_model, nhead, num_encoder_layers, num_decoder_layers)

# 假设输入和目标序列
input_sequence = torch.randn(seq_len, num_channels, width, height)
target_sequence = torch.randn(seq_len, num_channels, width, height)

# 前向传播
predicted_sequence = model(input_sequence, target_sequence)

print(predicted_sequence.shape)  # 输出预测序列的形状

内插：

import torch
import torch.nn as nn

class VideoFrameInterpolator(nn.Module):

    def _generate_positional_encoding(self, max_len, d_model):
        """生成位置编码"""
        positional_encoding = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        
        positional_encoding[:, 0::2] = torch.sin(position * div_term)
        positional_encoding[:, 1::2] = torch.cos(position * div_term)

        return positional_encoding


    def __init__(self, num_channels, width, height, total_seq_len, d_model, nhead, num_encoder_layers, num_decoder_layers):
        super(VideoFrameInterpolator, self).__init__()
        # 其他初始化代码保持不变



        super(VideoFrameInterpolator, self).__init__()

        self.total_seq_len = total_seq_len
        self.d_model = d_model

        # 将输入帧转换为模型可以处理的维度
        self.linear_in = nn.Linear(num_channels * width * height, d_model)

        # 初始化位置编码
        self.positional_encoding = self._generate_positional_encoding(total_seq_len, d_model)

        # Transformer模型
        self.transformer = nn.Transformer(
            d_model=d_model, 
            nhead=nhead, 
            num_encoder_layers=num_encoder_layers,
            num_decoder_layers=num_decoder_layers
        )

        # 将Transformer的输出转换回帧的形状
        self.linear_out = nn.Linear(d_model, num_channels * width * height)

    def forward(self, start_frame, end_frame):
        # 对起始帧和结束帧进行编码
        start_frame_encoded = self.linear_in(start_frame.view(-1, num_channels * width * height)) + self.positional_encoding[0]
        end_frame_encoded = self.linear_in(end_frame.view(-1, num_channels * width * height)) + self.positional_encoding[-1]

        # 对于解码器，我们初始化一个空的序列用于生成插值帧
        # 在训练时，这可以替换为真实的目标序列
        decoder_input = torch.zeros(self.total_seq_len - 2, start_frame.size(0), self.d_model, device=start_frame.device)
        decoder_input = decoder_input + self.positional_encoding[1:-1]

        # 编码器输入是起始帧和结束帧
        encoder_input = torch.cat([start_frame_encoded.unsqueeze(0), end_frame_encoded.unsqueeze(0)], dim=0)

        # Transformer模型生成插值帧
        interpolated_frames = self.transformer(encoder_input, decoder_input)

        # 转换回原始帧的形状
        interpolated_frames = self.linear_out(interpolated_frames)
        return interpolated_frames.view(-1, self.total_seq_len - 2, num_channels, width, height)

# 创建模型实例和测试数据
# [剩余部分与之前代码相同]

自监督学习(Self-supervised Learning)

自监督学习主要是利用辅助任务（pretext）从大规模的无监督数据中挖掘自身的监督信息，通过这种构造的监督信息对网络进行训练，SSL是无监督训练的一类，或者也可以归为无监督训练。

在ICLR2020的主题演讲中，Yann LeCun将SSL定义为：An analogous process to completing missing information(reconstruction)

他提出了几个变体：

• 从任何其他部分预测输入的任何部分；
• 从过去预测未来；
• 从可见预测不可见；
• 从所有可用部分预测任何被遮挡、掩盖或损坏的部分。

举个例子：随机的将图片中的一部分删掉，然后利用剩余的部分来预测扣掉的部分，只有模型真正读懂了这张图所代表的含义，才能有效的进行补全。

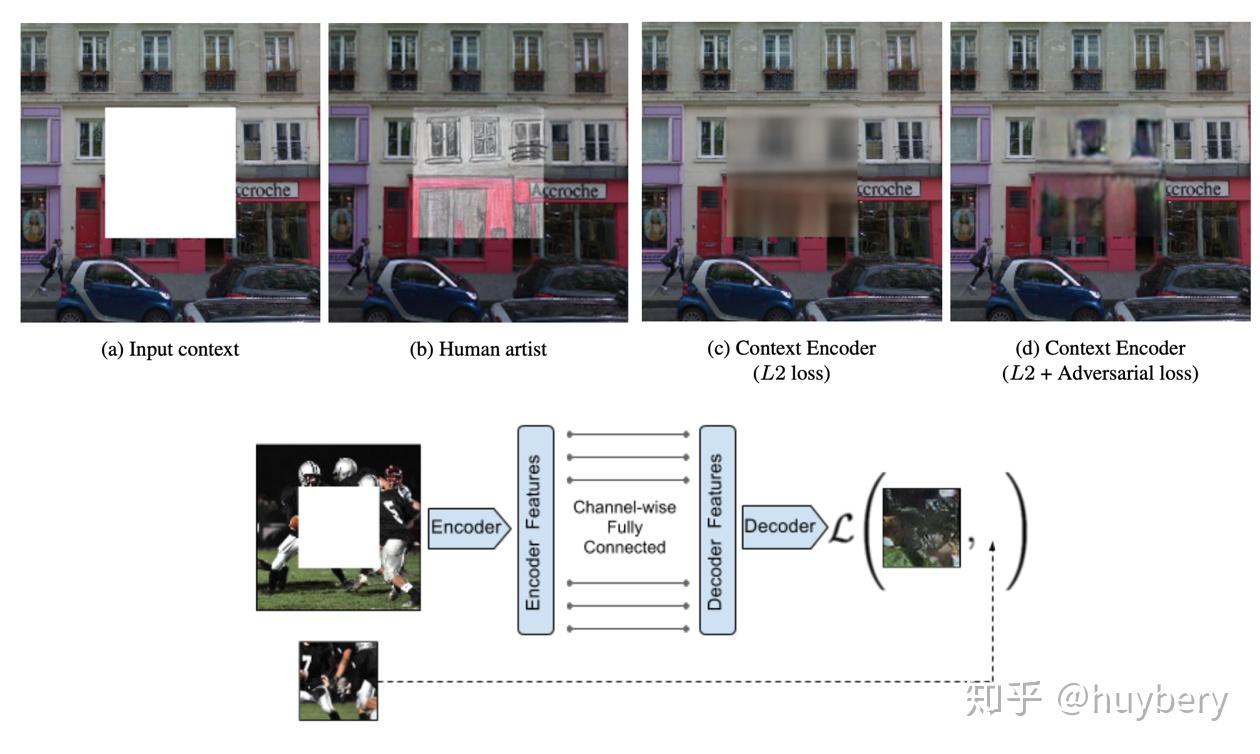
详细的可以阅读：
https://zhuanlan.zhihu.com/p/108906502
《A Survey on Self-supervised Learning: Algorithms, Applications, and Future Trends》

概念知识

回归（regression）是什么

回归和分类都是对变量之间的关系进行建模的方法

回归预测的变量是数值型变量。例如预测用户的收入（4千，2万，10万……），预测员工的通勤距离（500m，1km，2万里……），预测患肺癌的概率（1%，50%，99%……）

分类预测的变量是分类型变量。例如如预测用户的性别（男、女），预测月季花的颜色（红、白、黄……），预测是否患有肺癌（是、否）

但分类和回归可以相互转换。我们可以用回归模型先预测出患肺癌的概率，然后再给定一个阈值，例如50%，概率值在50%以下的人划为没有肺癌，50%以上则认为患有肺癌。

线性回归，就是假设自变量和因变量之间呈线性关系。

名词解释

regression:回归

training data set = training set:训练数据集/训练集

sample = data point = data instance:样本/数据点/数据样本

label = target:标签/目标

feature = covariate:特性/协变量

translation:平移

gradient descent:梯度下降

minibatch stochastic gradient descent:小批量随机梯度下降

batch size:批量大小

hyperparameter tuning:调参

trade-off:取舍/权衡
原文链接

深度学习领域中的几个指标也相同。

主要的指标有如下四个：

（1）精度：自然精度是一个模型最根本的衡量指标，如果一个模型精度不高，再快，再绿色环保也无济于事。基本上所有刷榜的工作都是用其他所有指标换精度：比如用更深的网络就是用memory和computation换精度。然而到了实际应用中，尤其是部署侧，工程师越来越多的用一些方法适当的减少精度从而换取更小的内存占用或者运算时间

（2）内存：Out Of Memory Error恐怕是炼丹师最常见的情况了。内存（或者说可以高效访问的存储空间）的尺寸是有限的，如果网络训练需要的内存太大了，可能程序直接就报错了，即使不报错，也需要把内存中的数据做个取舍，一部分存到相对较慢的存储介质中（比如host memory）。

(3) 通信：随着网络规模越来越大，分布式训练已经是state-of-the-art的网络模型必不可少的部分（你见过谁用单卡在ImageNet训练ResNet50？），在大规模分布式系统，通信带宽比较低，相比于computation或者memory load/sotre，network communication会慢很多，如果可以降低通信量，那么整个网络的训练时间就会有大幅减少：这样研究员就不会借口调参，实际上把模型往服务器上一扔自己就跑出去浪了。(资本家狂喜)

（4）计算：虽然我们用的是计算机，但实际上恐怕只有很少的时间用于计算(computation)了，因为大多数时间都在等待数据的读取或者网络通信，不过即便如此，对于一些计算密集型的神经网络结构（比如BERT，几乎都是矩阵乘法），制约我们的往往是设备的计算能力（FLOPS），即每秒钟可以处理多少浮点计算。

常见的trade-off:
（1）计算换内存
（2）通信换内存
（3）计算换通信
（4）显存换计算
（5）精度换计算/内存/通信

孪生网络（Siamese newtowk）:原文链接

hard/soft physical constraints

在深度学习与计算流体力学领域中，”hard physical constraints”（硬物理约束）指的是在模型建立和求解过程中必须严格遵守的物理规律或约束条件。这些约束条件通常是基于问题的物理性质和基本定律，例如质量守恒、能量守恒、动量守恒等。

在计算流体力学中，硬物理约束可能包括以下方面：

1. 质量守恒：流体的入口和出口质量流量必须保持平衡。
2. 动量守恒：流体中的动量转移满足牛顿第二定律。
3. 能量守恒：流体中的能量转移满足能量守恒定律。
4. 不可压缩性：在不可压缩流体模拟中，流体密度保持恒定。
5. 边界条件：在模拟中，需要定义适当的边界条件以满足问题的物理要求。

在深度学习中，硬物理约束指的是将物理约束直接嵌入到深度学习模型中的方法。通过在模型的设计和训练过程中引入这些硬物理约束，可以更好地确保生成的结果符合物理定律和约束条件。这有助于提高模型的物理合理性和实用性。

总而言之，硬物理约束是指在深度学习与计算流体力学中必须遵守的严格物理规律和约束条件，确保模型与实际物理系统的一致性。

---

在深度学习与计算流体力学领域中，”soft physical constraints”（软物理约束）指的是在模型建立和求解过程中考虑的物理规律或约束条件，但其遵守程度可以有一定的灵活性或容忍度。与硬物理约束相比，软物理约束更加柔性，允许在一定程度上违背或放宽约束条件，以获得更好的模型拟合或求解结果。

软物理约束通常是通过引入损失函数或惩罚项来实现的，以在模型训练或优化过程中对违反约束条件进行惩罚或限制。这样可以在尽量满足物理规律的同时，允许一定程度的误差或适应性，以提高模型的灵活性和适应性。

在计算流体力学中，软物理约束可以包括以下方面：

1. 不稳定流动约束：在流体模拟中，允许一定程度的不稳定性或涡旋生成，而不要求完全消除或压制。
2. 数值耗散约束：在数值模拟中，可以引入一定的耗散项或平滑操作，以减少数值震荡或不稳定性，同时保持一定的数值精度。
3. 材料参数估计约束：在模型中，对材料参数或未知参数的估计可以具有一定的容忍度，以考虑实际系统的不确定性或噪声。

总而言之，软物理约束是在深度学习与计算流体力学中考虑的相对柔性的物理规律或约束条件。通过在模型的训练或优化过程中引入相应的损失函数或惩罚项，可以在一定程度上允许约束条件的违背，以提高模型的适应性和灵活性。

Non-intrusive Reduced Order Model(非侵入式降阶模型)

在深度学习中，“Non-intrusive Reduced Order Model”（非侵入式降阶模型）是一种用于减少高维问题复杂性的建模方法。它的目标是通过将高维问题映射到低维空间中，以降低计算成本和内存需求，同时保持问题的关键特征和准确性。

传统的减少高维问题复杂性的方法通常是通过降阶技术，如主成分分析（PCA）或奇异值分解（SVD），来提取问题的主要模式或特征，并建立一个低维模型。然而，这些方法通常需要对问题的物理方程进行修改或重新建模，因此被称为“侵入式模型”。

相比之下，非侵入式降阶模型采用机器学习技术，如深度学习，通过学习数据集中的模式和关系来构建低维模型，而无需对物理方程进行修改。它可以通过将输入数据映射到低维表示空间，并使用深度神经网络来学习映射函数，从而实现降维和建模。

非侵入式降阶模型在减少计算负担、加速模拟和优化高维问题方面具有潜力。它可以在保持问题关键特征和准确性的同时，提供更高效的模型求解和分析能力。这种方法在多个领域中得到应用，包括流体力学、结构分析、图像处理等。

需要注意的是，非侵入式降阶模型的性能和适用性取决于所选择的机器学习算法、数据集质量和训练过程等因素。因此，在具体应用中，需要根据问题的特点和需求，选择适当的非侵入式降阶方法和技术，以获得准确和高效的模型求解结果。

---

在”Non-intrusive Reduced Order Model”中，”Non-intrusive”（非侵入式）是指建立降阶模型时，不需要对原始问题进行修改或重新建模的特性。它强调了在建立模型时不需要修改问题的物理方程或引入额外的信息，而是通过使用外部数据或机器学习方法来近似原始问题。

传统的降阶方法通常要求对问题的物理方程进行简化或修改，以提取主要模式或减少系统的自由度。这种方法被称为”侵入式”，因为它们需要对原始问题进行干预或修改。

相比之下，”Non-intrusive Reduced Order Model”使用非侵入式的方法来构建降阶模型。它不需要修改原始问题的物理方程，而是利用外部数据或机器学习技术来建立一个近似模型。这意味着原始问题的求解过程保持不变，只是在模拟或优化中引入降维的近似模型。

非侵入式方法的优点在于它们能够在保持原始问题的准确性和复杂性的同时，减少计算成本和内存需求。它们提供了一种灵活的方式来处理高维问题，同时提供较低的计算复杂度和更高的模拟速度。

总而言之，”Non-intrusive Reduced Order Model”中的”Non-intrusive”表示在构建降阶模型时不需要修改原始问题的物理方程或引入额外信息，而是通过使用外部数据或机器学习技术来近似原始问题。这种方法提供了一种非侵入性、灵活性和高效性的方式来处理高维问题的模拟和优化。

矩阵计算

在深度学习相关的资料里面，标量就表示一个数，向量是由多个数组成的。

常规的导数求导没有什么难度，现在将导数扩展到向量，会出现四种情况：

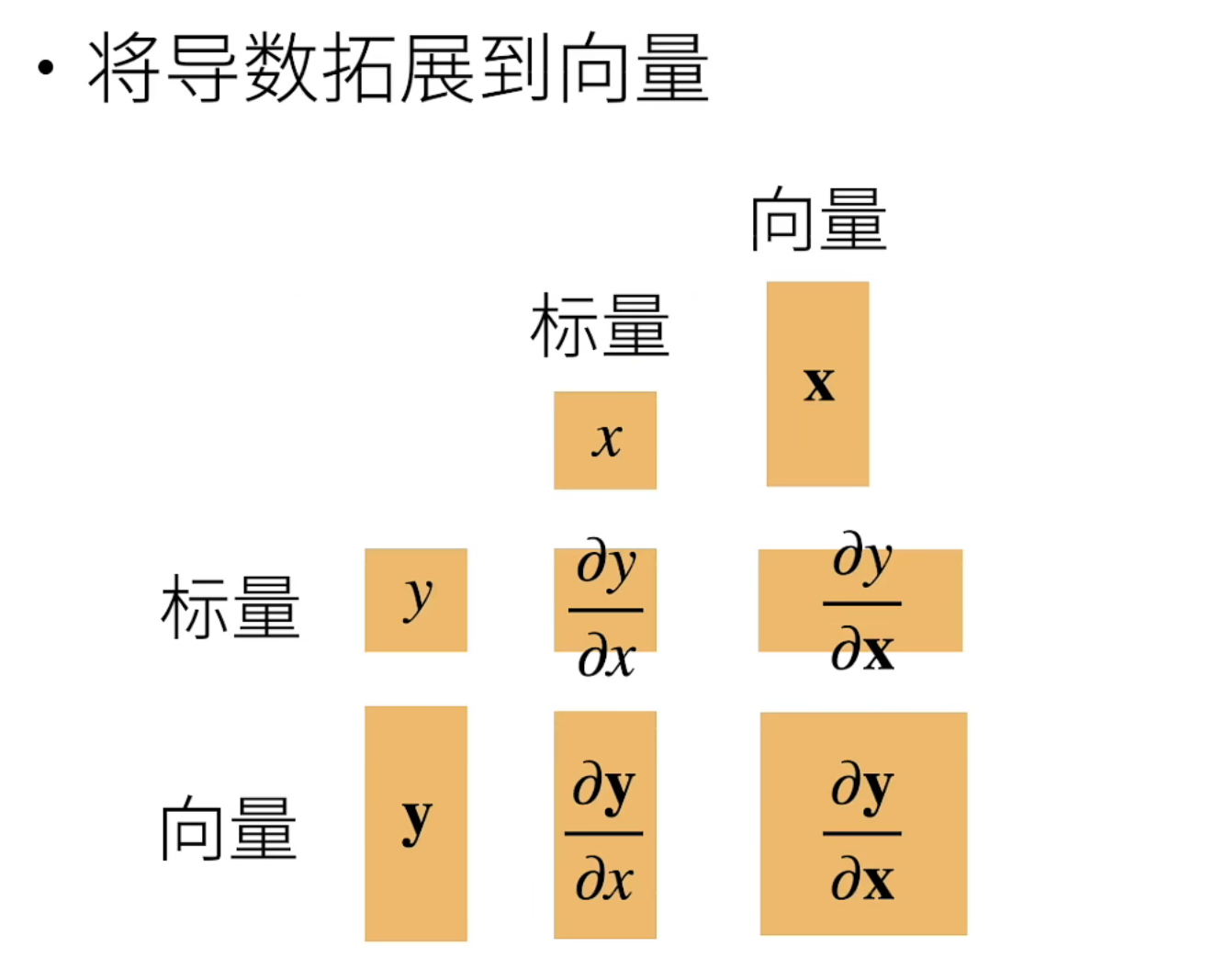
y为标量或向量；x为标量或向量

1、标量求导就不说了，高中常识；
2、y是标量，x是向量的情况。实际上就是y=f(x1,x2,…,xn)的意思。拿y=f(x1,x2)为例解释，有一个三维坐标轴体系，水平面的横轴和竖轴分别是x1、x2，立面上的轴是y，水平面上任意一个点(x1,x2)都对应y轴上的一个点，很明显这就是一个面，因此他的导数是一个向量，所以结果是横着写的。

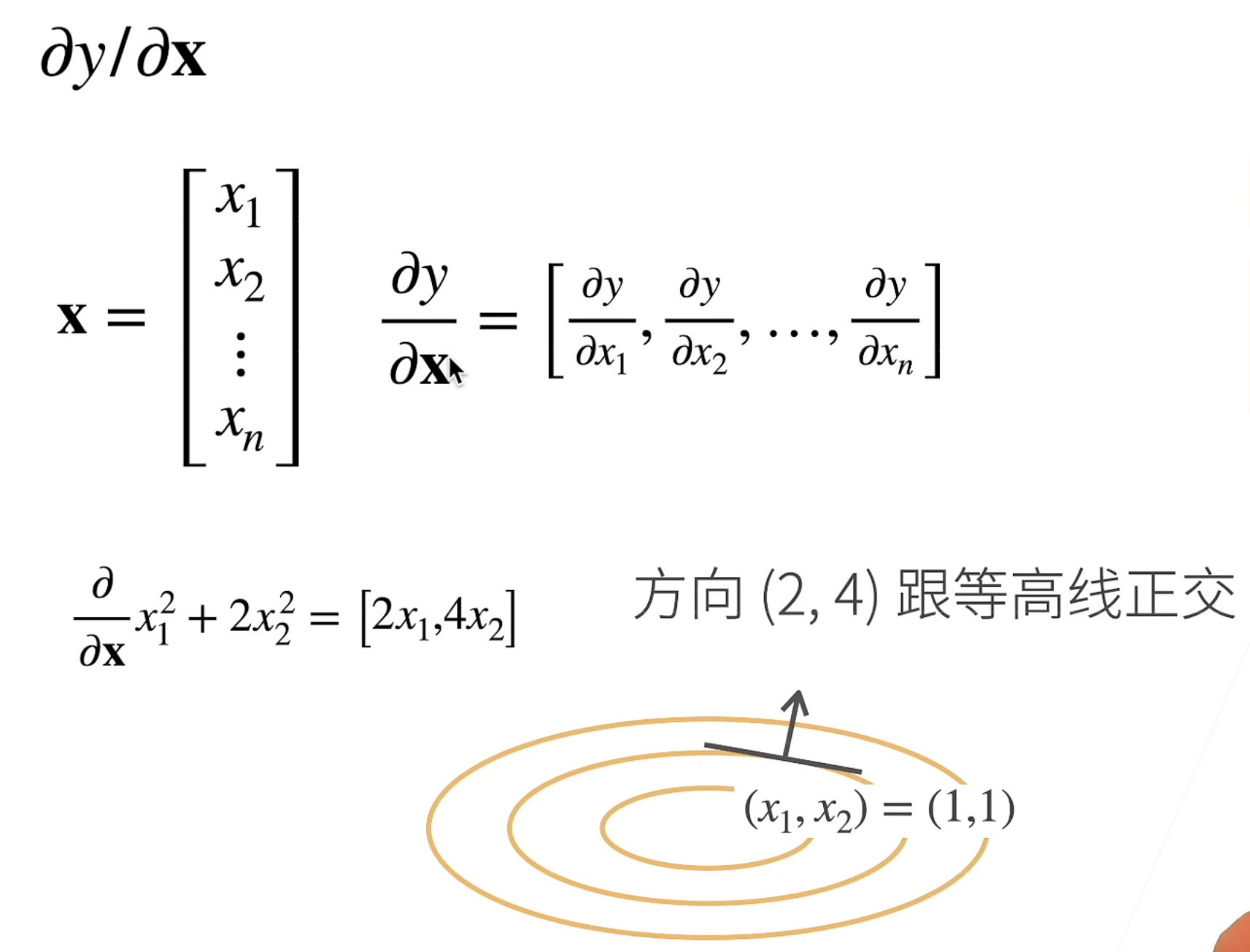
3、y是向量，x是标量的情况。这实际上就是【y1,y2,…,yn】=【f(x1),f(x2),…,f(xn)】，对x求导就是求出y=yi时那一个点上的斜率，结果是标量，所以结果是竖着写的。

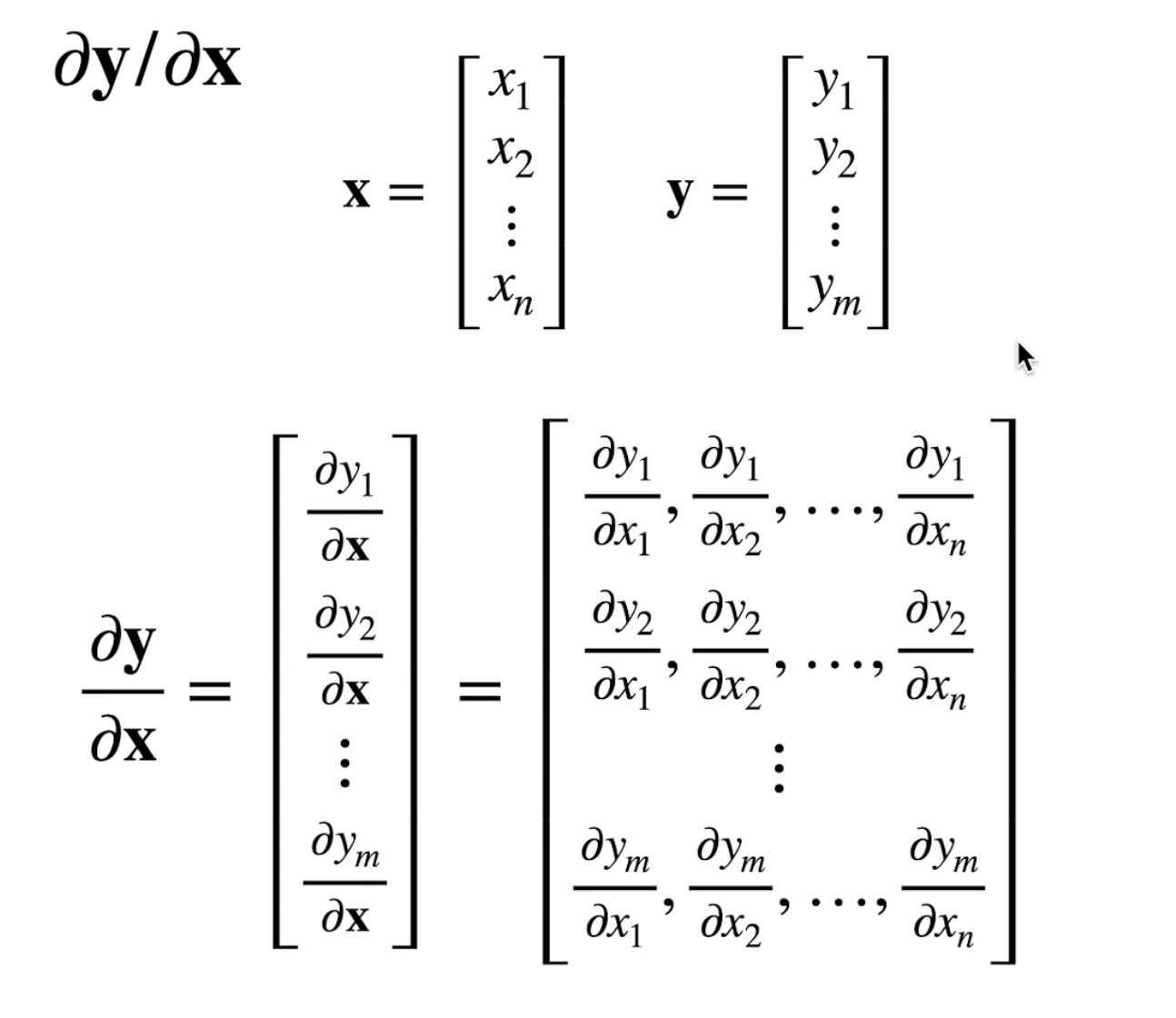
4、y、x都是向量的情况。根据上面描述，求导实际上就是求出了y=yi时，那一个平面形状边缘上的向量，因此是横着写的。

---

关于动手学习深度学习，自动微分章节里面2.5.1例子的理解原链接

我们对函数关于列向量x求导，假设变量x为

可以容易的得到y是标量，且值为28.
参考上面提到的四种情况，求导结果应该为向量。

可以把看作是，求导后为，那么带入，最后的结果为

还有另外一种理解方式，把向量里面的值用代替，那么，然后再对每个分量进行求导，即可得到梯度。，把的值带入，得到最终的结果

同样的，对于该小节下面的例子

x.grad.zero_()  //  x梯度清零，x=[0,1,2,3]
y=x.sum()     // 按上面的方法，y=x1+x2+x3+x4
y.backward()  
x.grad

x梯度清零，

按上面的方法，

损失函数和梯度下降的关系

以线性回归为例，模型为：。
其中,是我们要求的参数，深度学习大多数时候就是要把参数求出来

损失函数：为了量化目标的实际值与预测值之间的差距。以平方损失函数为例，带入样本就可以得到差距。损失函数值越小，说明效果越好。我们就是要找到使损失函数值最小的那组参数

梯度下降就是让我们找到那组参数的优化算法

下面举一个梯度下降法的使用例子。例子来源

上图中步骤4稍微说明下，是单独对每个变量求偏导数后得到的，这样结果就是一个标量而不是向量。具体的过程看下图。

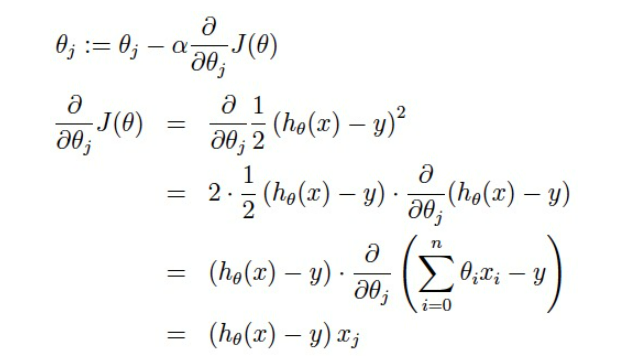
当梯度下降的距离小于给定的值，就停止计算，得到的参数值就是最终的结果。

深度学习为什么要加入隐藏层

让特征可以更好的进行线性划分

原链接

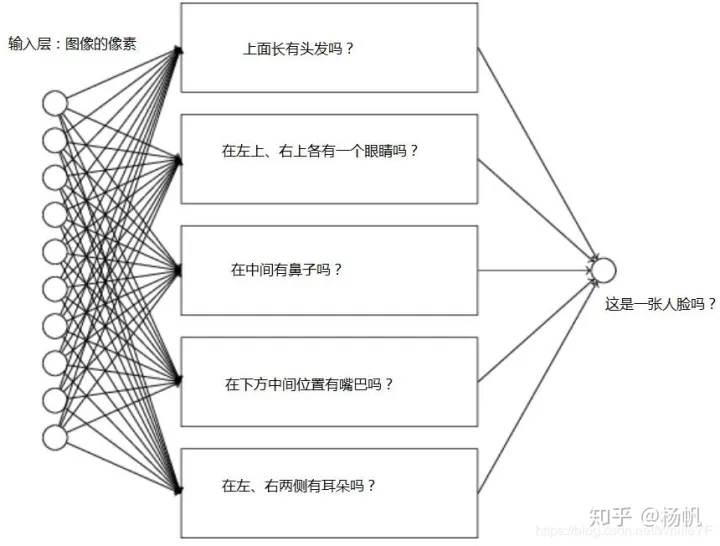
例如区分以下三张图片哪个是人脸，也就是人脸识别，神经网络模型应该怎么建立呢？为了简单起见，输入层的每个节点代表图片的某个像素，个数为像素点的个数，输出层简单地定义为一个节点，标示是还是不是。

那么隐含层怎么分析呢？ 我们先从感性地角度认识这个人脸识别问题，试着将这个问题分解为一些列的子问题，比如，

在上方有头发吗？

在左上、右上各有一个眼睛吗？

在中间有鼻子吗？

在下方中间位置有嘴巴吗？

在左、右两侧有耳朵吗？

假如对以上这些问题的回答，都是“yes”，或者大部分都是“yes”，那么可以判定是人脸，否则不是人脸。但是，这种判断忽略了某些特殊情况，比如某个人没有长头发，某个人的左半边脸被花丛遮挡了等等，等处在这些环境中时，这种方法的判断可能会有问题。

承上，将原问题分解为子问题的过程如果用神经网络来表达的话，可以这样表示，方框表示为某个子网络：

以上每个子网络，还可以进一步分解为更小的问题，比如判断左上是一个眼睛吗的问题，可以分解为：

有眼球吗？
有眼睫毛吗？
有虹膜吗？
…

以上，这个子网络还可以进一步分解，.一层又一层地分解，直到，回答的问题简单到能在一个单独的神经元上被回答。

这种带有两个或多个隐含层的神经网络，称为深度神经网络，deep neural networks，简称为 DNN。

为什么要使用编码器和解码器

编码器是压缩数据，解码器是还原数据。一压一还意义何在？

编码：捕获了输入数据的最重要的特征，并且舍弃了一些不重要的细节；数据被压缩后，对硬件的负担也变小了。

解码：使重建的数据尽可能接近原始输入数据。

训练过程中，Convolutional Autoencoder (CAE)通常使用重构损失（比如均方误差）来衡量重建的数据和原始输入数据的差异，然后通过反向传播和优化算法来不断调整网络参数，使得重构损失最小。

总的来说，Convolutional Autoencoder (CAE)的主要步骤是：输入数据 —> 编码器（卷积+池化）—> 潜在特征表示 —> 解码器（上采样+卷积）—> 输出数据（重建的数据）。

预训练和传统训练的区别

预训练是指在一个大规模通用数据集上先训练模型，使其学习数据的通用特征表示。这个过程通常是无监督或自监督的（无需人工标注标签）。例如：

在自然语言处理（NLP）中，BERT 模型通过预训练学习词语、句子的上下文关系。

传统训练时是针对特定任务（如时间序列异常检测），直接在目标数据集上训练模型。

微调往往和预训练结合，在目标数据集上，用少量标注数据调整预训练模型的参数，使其适应具体任务（如异常检测）。

熵、信息熵、相对熵、KL散度、交叉熵损失、softmax

softmax

softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持 可导的性质

熵和信息熵

熵和信息熵本质是一个东西，就是换了个说法而已。

熵：在信息论中则表示事务的不确定性。信息量与信息熵是相对的，告诉你一件事实，你获取了信息量，但减少了熵。或者说，得知一件事实后信息熵减少的量，就是你得到的这个事实所包含的信息的量。

熵的公式：

n:表示随机变量可能的取值
x:表示随机变量
P(x):表示随机变量x的概率函数

log以10，2或者e为底，对结果熵的判断没有影响

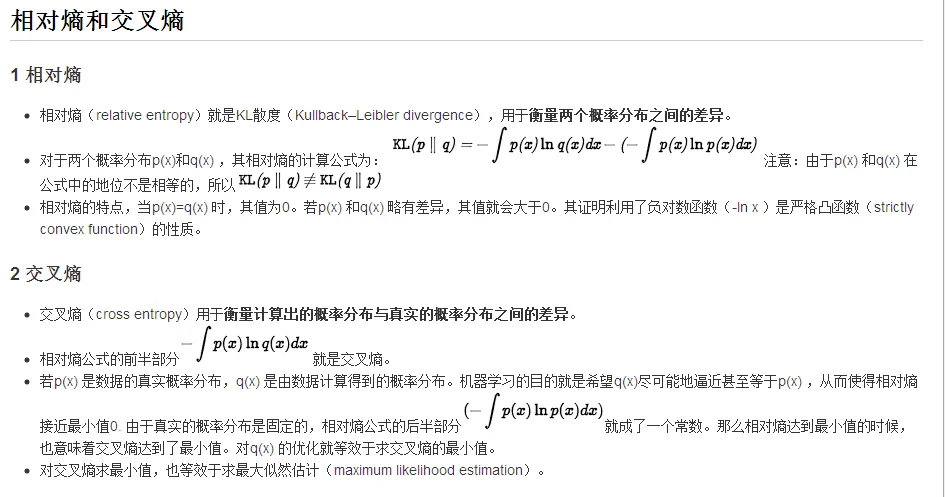
相对熵和交叉熵

相对熵就是KL散度

用于衡量两个概率分布之间的差异。

我们把上面的公式展开

$$\begin{aligned} D_{K L}(p \| q)&=\sum_{i=1}^{n} p\left(x_{i}\right) \log \left(\frac{p\left(x_{i}\right)}{q\left(x_{i}\right)}\right) \\ &=\sum_{i=1}^{n}p(x_{i})l o g\,p(x_{i})-\sum_{i=1}^{n}p(x_{i})l o g q(x_{i})\\ &= -(-\sum_{i=1}^{n}p(x_{i})l o g\,p(x_{i})) - \sum_{i=1}^{n}p(x_{i})l o g q(x_{i}) \\ &= -H(P) + H(P,Q) \\ &= H(P,Q) -H(P) \\ &= 交叉熵 - 信息熵 \\ \end{aligned}$$

p(x)表示真实概率分布，q(x)表示预测概率分布
交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近，即拟合的更好。

当p(x)=q(x)时，相对熵为0
相对熵越小越好，相对熵和交叉熵的差距只有一个常数。那么相对熵达到最小值的适合，也就是交叉熵达到最小的时候。所以对q(x)的优化等效于求交叉熵的最小值，交叉熵的最小值也就是求最大似然估计

似然函数、极大似然函数

p(x|θ)也是一个有着两个变量的函数。如果，你将θ设为常量，则你会得到一个概率函数（关于x的函数）；如果，你将x设为常量你将得到似然函数（关于θ的函数）。

概率描述的是：指定参数后，预测即将发生事件的可能性；

似然描述的是：在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计；

极大似然估计是在已知一堆数据和分布类型的前提下，反推最有可能的参数是什么，也就是“它最像这个分布哪组参数下表现出来的数据”。

举个例子：

将抽球结果作为，即离散随机变量，设白球为
，黑球为 。假设抽到白球的概率为 ， 即是未知的需要通过极大似然估计得出的参数。

写出一次预测的似然函数：

$$L(\theta|x)=f(x|\theta)=P(x,\theta)=\theta^{x}*{(1-\theta)}^{(1-x)}$$

这里解释下为什么是这样的：

如果抽到的是白球，就是,密度函数是，带入公式没有问题；
如果抽到的是黑球，就是,密度函数是，带入公式没有问题；

对于二项分布，出现符合观测情况的，白球出现7次，黑球出现三次的概率密度函数为
$P(X,\theta)=P(x1,\theta)P(x2,\theta)..\cdot P(x10,\theta)=\theta^{7}*(1-\theta)^{3}$

写成似然函数形式为：

似然函数和交叉熵的关系

为了求最大的似然函数，我们往往取对数，最后发现二分类的极大似然函数和二分类交叉熵相同

原文链接

训练集、验证集、测试集

在深度学习中，通常会将数据集划分为三个部分：训练集（Training Set）、验证集（Validation Set）和测试集（Test Set）。这三个数据集的主要目的是用于模型的训练、调优和评估。

1. 训练集（Training Set）：训练集是用来训练深度学习模型的数据集。模型在训练集上进行反向传播和参数更新，通过不断调整模型参数来拟合训练数据中的模式和规律。

2. 验证集（Validation Set）：验证集是用于模型调优和选择最佳模型的数据集。在训练过程中，通过在验证集上评估模型的性能，可以及时监测模型的泛化能力和过拟合情况。通过对模型的超参数和结构进行调整，选择在验证集上表现最佳的模型。

3. 测试集（Test Set）：测试集是用于最终评估模型性能的数据集。它是在训练和验证过程中没有被使用过的独立数据集。通过在测试集上评估模型的性能，可以获得对模型真实泛化能力的评估结果。测试集的结果可以用来判断模型的性能是否达到了预期要求。

区别：

• 训练集用于模型的训练，通过反向传播和参数更新来拟合数据集。
• 验证集用于模型的调优和选择最佳模型，通过评估模型在验证集上的性能来进行超参数和结构的调整。
• 测试集用于最终评估模型的性能，检验模型的泛化能力。

这三个数据集的划分有助于确保模型在未见过的数据上具有较好的泛化能力，同时避免模型在训练过程中过度拟合训练数据。通常，数据集的划分比例是将数据的大部分分配给训练集（70-80%），一小部分用于验证集（10-15%），剩余的部分用于测试集（10-15%）。

欠拟合、过拟合

原文链接

训练误差：模型在训练数据集上计算得到的误差

泛化误差：模型应用在同样从原始样本的分布中抽取的无限多数据样本时，模型误差的期望。

度量泛化能力的好坏，最直观的表现就是模型的过拟合（overfitting）和欠拟合（underfitting）。过拟合和欠拟合是用于描述模型在训练过程中的两种状态。一般来说，训练过程会是如下所示的一个曲线图。

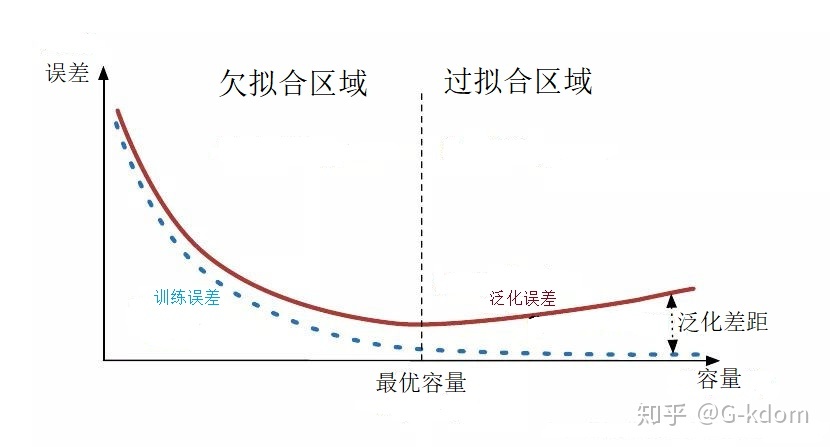
训练刚开始的时候，模型还在学习过程中，处于欠拟合区域。随着训练的进行，训练误差和测试误差都下降。在到达一个临界点之后，训练集的误差下降，测试集的误差上升了，这个时候就进入了过拟合区域——由于训练出来的网络过度拟合了训练集，对训练集以外的数据却不work。

1. 什么是欠拟合

欠拟合是指模型不能在训练集上获得足够低的误差。换句换说，就是模型复杂度低，模型在训练集上就表现很差，没法学习到数据背后的规律。

1. 如何解决欠拟合
   欠拟合基本上都会发生在训练刚开始的时候，经过不断训练之后欠拟合应该不怎么考虑了。但是如果真的还是存在的话，可以通过增加网络复杂度或者在模型中增加特征，这些都是很好解决欠拟合的方法。

2. 什么是过拟合

过拟合是指训练误差和测试误差之间的差距太大。换句换说，就是模型复杂度高于实际问题，模型在训练集上表现很好，但在测试集上却表现很差。模型对训练集”死记硬背”（记住了不适用于测试集的训练集性质或特点），没有理解数据背后的规律，泛化能力差。

1. 为什么会出现过拟合

造成原因主要有以下几种：
1、训练数据集样本单一，样本不足。如果训练样本只有负样本，然后那生成的模型去预测正样本，这肯定预测不准。所以训练样本要尽可能的全面，覆盖所有的数据类型。
2、训练数据中噪声干扰过大。噪声指训练数据中的干扰数据。过多的干扰会导致记录了很多噪声特征，忽略了真实输入和输出之间的关系。
3、模型过于复杂。模型太复杂，已经能够“死记硬背”记下了训练数据的信息，但是遇到没有见过的数据的时候不能够变通，泛化能力太差。我们希望模型对不同的模型都有稳定的输出。模型太复杂是过拟合的重要因素。

1. 如何防止过拟合

要想解决过拟合问题，就要显著减少测试误差而不过度增加训练误差，从而提高模型的泛化能力。我们可以使用正则化（Regularization）方法。那什么是正则化呢？正则化是指修改学习算法，使其降低泛化误差而非训练误差。

常用的正则化方法根据具体的使用策略不同可分为：（1）直接提供正则化约束的参数正则化方法，如L1/L2正则化；（2）通过工程上的技巧来实现更低泛化误差的方法，如提前终止(Early stopping)和Dropout；（3）不直接提供约束的隐式正则化方法，如数据增强等。

回归自回归是什么意思

回归（Regerssion）

• 为一个或多个自变量与因变量之间关系建模的一类方法。 在自然科学和社会科学领域，回归经常用来表示输入和输出之间的关系。 在机器学习领域中的大多数任务通常都与预测（prediction）有关。 当我们想预测一个数值时，就会涉及到回归问题。
• 找出一堆无规律数据中的规律。

自回归（Autoregressive）

是统计上一种处理时间序列的方法，用同一变量例如到来预测，并假设它们为一线性关系。用来预测，而不是用来预测

学习率、batchsize、batch、epoch的区别

1. epoch:一个Epoch就是将所有训练样本训练一次的过程。然而，当一个Epoch的样本（也就是所有的训练样本）数量可能太过庞大（对于计算机而言），就需要把它分成多个小块，也就是就是分成多个Batch 来进行训练。
2. Batch（批 / 一批样本）:将整个训练样本分成若干个Batch。
3. Batch Size:每批样本的大小。
4. Iteration:训练一个Batch就是一次Iteration（这个概念跟程序语言中的迭代器相似）

Batch Size定义：一次训练所选取的样本数。

Batch Size的大小影响模型的优化程度和速度。同时其直接影响到GPU内存的使用情况，假如GPU内存不大，该数值最好设置小一点。

为什么要提出Batch Size?

在没有使用Batch Size之前，这意味着网络在训练时，是一次把所有的数据（整个数据库）输入网络中，然后计算它们的梯度进行反向传播，由于在计算梯度时使用了整个数据库，所以计算得到的梯度方向更为准确。但在这情况下，计算得到不同梯度值差别巨大，难以使用一个全局的学习率，所以这时一般使用Rprop这种基于梯度符号的训练算法，单独进行梯度更新。

在小样本数的数据库中，不使用Batch Size是可行的，而且效果也很好。但是一旦是大型的数据库，一次性把所有数据输进网络，肯定会引起内存的爆炸。所以就提出Batch Size的概念。

Batch Size合适的优点：

1、通过并行化提高内存的利用率。就是尽量让你的GPU满载运行，提高训练速度。

2、单个epoch的迭代次数减少了，参数的调整也慢了，假如要达到相同的识别精度，需要更多的epoch。

3、适当Batch Size使得梯度下降方向更加准确。

Batch Size从小到大的变化对网络影响

1、没有Batch Size，梯度准确，只适用于小样本数据库

2、Batch Size=1，梯度变来变去，非常不准确，网络很难收敛。

3、Batch Size增大，梯度变准确，

4、Batch Size增大，梯度已经非常准确，再增加Batch Size也没有用

注意：Batch Size增大了，要到达相同的准确度，必须要增大epoch。

GD（Gradient Descent）：就是没有利用Batch Size，用基于整个数据库得到梯度，梯度准确，但数据量大时，计算非常耗时，同时神经网络常是非凸的，网络最终可能收敛到初始点附近的局部最优点。

SGD（Stochastic Gradient Descent）：就是Batch Size=1，每次计算一个样本，梯度不准确，所以学习率要降低。

mini-batch SGD：就是选着合适Batch Size的SGD算法，mini-batch利用噪声梯度，一定程度上缓解了GD算法直接掉进初始点附近的局部最优值。同时梯度准确了，学习率要加大

学习率和batch对学习效果的影响

学习率和batch对学习效果的影响

为什么把连续性特征离散化，离散化有何好处

数据离散化的原因主要有以下几点：

1、算法需要

比如决策树、朴素贝叶斯等算法，都是基于离散型的数据展开的。如果要使用该类算法，必须将离散型的数据进行。有效的离散化能减小算法的时间和空间开销，提高系统对样本的分类聚类能力和抗噪声能力。

2、离散化的特征相对于连续型特征更易理解，更接近知识层面的表达

比如工资收入，月薪2000和月薪20000，从连续型特征来看高低薪的差异还要通过数值层面才能理解，但将其转换为离散型数据（底薪、高薪），则可以更加直观的表达出了我们心中所想的高薪和底薪。

3、可以有效的克服数据中隐藏的缺陷，使模型结果更加稳定

离散化的优势

1. 离散特征的增加和减少都很容易，易于模型的快速迭代；

2. 稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；

3. 离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；

4. 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；

5. 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；

6. 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

7. 特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

深度学习的参数

参数是模型学习的各种权重和偏置。

如果x是输入，y是输出。那么k就是权重，b就是偏置。训练模型学的就是权重和偏置。

模型的大小通常是指模型参数的数量。一个模型参数的数量越多，模型就越大。

卷积神经网络（Convolutional Neural Networks，CNN）的参数主要体现在卷积层、全连接层和偏置项中。这些参数包括每个卷积核的权重、全连接层中各节点的权重以及每一层的偏置项。

以一个简单的CNN为例，该网络包含一个卷积层和一个全连接层：

卷积层：假设输入图像大小为28x28x1（例如，灰度图像），卷积核大小为5x5，卷积核的数量为32。那么，卷积层的参数数量就是5x5x1x32（卷积核的宽度 x 卷积核的高度 x 输入的通道数 x 卷积核的数量）=800。（因为卷积核中的每个数目都是参数，不是固定的。所有卷积核的每一项都是参数）另外，每个卷积核都有一个对应的偏置项，所以卷积层的偏置项数量就是32。因此，卷积层的总参数数量为800+32=832。

全连接层：假设卷积层的输出通过池化和展平操作后，大小为512，然后连接到全连接层，全连接层的节点数量为10（例如，用于10分类的问题）。那么，全连接层的参数数量就是512x10=5120。同样，全连接层的偏置项数量就是10。因此，全连接层的总参数数量为5120+10=5130。

因此，这个CNN的总参数数量为832（卷积层）+5130（全连接层）=5962。这就是参数数量的计算方式。

为什么要做特征归一化/标准化

链接

总结：归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时，其对解决该问题就有正向作用，反之，就会起反作用。所以，“何时选择何种方法”取决于待解决的问题，即problem-dependent。

原因

1. 特征间的单位（尺度）可能不同，比如身高和体重，比如摄氏度和华氏度，比如房屋面积和房间数，一个特征的变化范围可能是
   [1000,10000]，另一个特征的变化范围可能是
   [−0.1,0.2]，在进行距离有关的计算时，单位的不同会导致计算结果的不同，尺度大的特征会起决定性作用，而尺度小的特征其作用可能会被忽略，为了消除特征间单位和尺度差异的影响，以对每维特征同等看待，需要对特征进行归一化。

2. 原始特征下，因尺度差异，其损失函数的等高线图可能是椭圆形，梯度方向垂直于等高线，下降会走zigzag路线，而不是指向local minimum。通过对特征进行zero-mean and unit-variance变换后，其损失函数的等高线图更接近圆形，梯度下降的方向震荡更小，收敛更快。

常用feature scaling方法

给定数据集，令特征向量为，维数为
，样本数量为，可构成
的矩阵，一列为一个样本，一行为一维特征

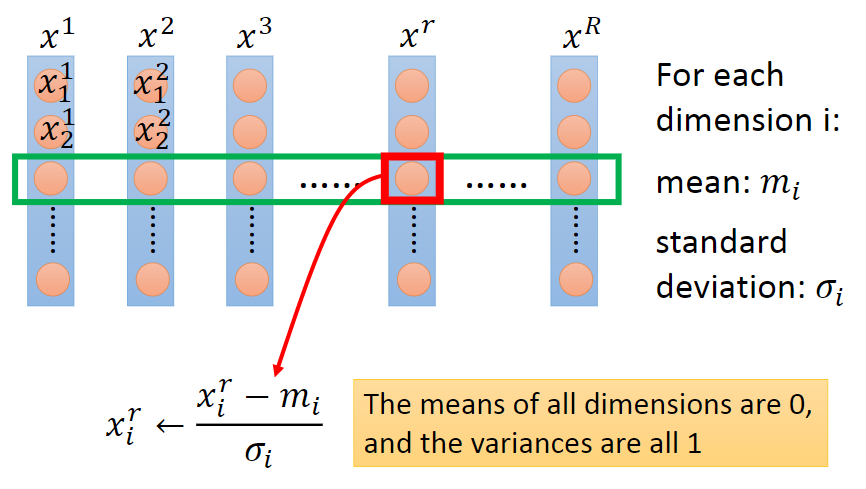
feature scaling的方法可以分成2类，逐行进行和逐列进行。逐行是对每一维特征操作，逐列是对每个样本操作，上图为逐行操作中特征标准化的示例。

计算方式上对比分析

前3种feature scaling的计算方式为减一个统计量再除以一个统计量，最后1种为除以向量自身的长度。

• 减一个统计量可以看成选哪个值作为原点，是最小值还是均值，并将整个数据集平移到这个新的原点位置
• 除以一个统计量可以看成在坐标轴方向上对特征进行缩放，用于降低特征尺度的影响，可以看成是某种尺度无关操作。缩放可以使用最大值最小值间的跨度，也可以使用标准差（到中心点的平均距离），前者对outliers敏感，outliers对后者影响与outliers数量和数据集大小有关，outliers越少数据集越大影响越小。
• 除以长度相当于把长度归一化，把所有样本映射到单位球上，可以看成是某种长度无关操作，比如，词频特征要移除文章长度的影响，图像处理中某些特征要移除光照强度的影响，以及方便计算余弦距离或内积相似度等。

线性神经网络

线性回归

线性回归基于几个简单的假设： 首先，假设自变量
和因变量之间的关系是线性的， 即可以表示为
中元素的加权和，这里通常允许包含观测值的一些噪声； 其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

线性回归的关键在于寻找最好的模型参数，需要两个东西：
（1）一种模型质量的度量方式：损失函数
（2）一种能够更新模型以提高模型预测质量的方法：优化算法

模型的优化过程就是：随机抽样一个小批量，它是由固定数量的训练样本组成的。 然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。 最后，我们将梯度乘以一个预先确定的正数，并从当前参数的值中减掉。

conda常用命令

1. 获取版本号

   conda --version
   // conda -V

2. 获取帮助

   conda --help
   conda -h

   查看某一命令的帮助，如update命令及remove命令

   conda update --help
   conda remove --help

3. 创建环境

   conda create --name your_env_name

创建制定python版本的环境

conda create --name your_env_name python=2.7
conda create --name your_env_name python=3
conda create --name your_env_name python=3.5

列举当前所有环境

conda info --envs
conda env list

进入某个环境

activate your_env_name

退出当前环境

deactivate 

复制某个环境

conda create --name new_env_name --clone old_env_name 

删除某个环境

conda remove --name your_env_name --all

遇到的问题

loss.backward()耗时严重

loss.backward()主要是计算梯度，为后面更新参数做准备，如果这一步耗时严重，要么是网络结构复杂，要么是计算图非常大。如果某个tensor的requires.grad属于被开启，那么就会为其分配一个计算图。

背景：

pde_data = torch.from_numpy(pd.read_csv(self.config.pde_data_path).values).float().to(self.device)

self.pde_Xs = [pde_data[:, i:i+1].requires_grad_() for i in range(self.config.X_dim)]

上面这段代码是读取数据后，然后开启requires_grad_()，但是它是对所有的数据都开启requires_grad_()，即使后面batch只使用了很小一部分数据，但是loss.backward()还是会计算这一部分，导致很慢。

正确的做法：
在取出batch的时候才为这些数据开启requires_grad_()

tensor必须在同一个设备上面

有时候需要把numpy转为tensor，再转回来。

可能会遇到不在同一个设备上面，需要阻断反向传播等。
下面给一个简单的例子：

// 把numpy转为tensor，再换为32位的（网络接受的是32位），在移动到同一个device上
predict = net(torch.from_numpy(XYT).float().to(config.device))

// tensor转换为numpy，除了要先放到cpu上，还需要阻断反向传播，requires_grad为false
predict = predict.cpu().detach().numpy()

深度学习代码解析

自定义激活函数并调用

import torch
import torch.nn as nn

# 定义一个自定义的激活函数
class CustomActivation(nn.Module):
    def __init__(self, a_init_value):
        super().__init__()
        self.a = nn.Parameter(torch.tensor(a_init_value))

    def forward(self, x):
        return 1.0 / (1.0 + torch.exp(-self.a * x))


# 定义一个网络层，其中使用了自定义的激活函数
class MyLayer(nn.Module):
    def __init__(self, input_size, output_size):
        super(MyLayer, self).__init__()
        self.linear = nn.Linear(input_size, output_size)
        self.custom_activation = CustomActivation(a_init_value=0.1)

    def forward(self, x):
        x = self.linear(x)
        x = self.custom_activation(x)
        return x

# 使用自定义的网络层
my_layer = MyLayer(10, 20)

# 随机生成一个输入数据
input_data = torch.randn(5, 10)

# 使用自定义的网络层进行前向传播
output_data = my_layer(input_data)

首先，我们从torch.nn模块中导入Module类，然后定义了一个新的类CustomActivation，这个类继承了Module类，所以它也是一个PyTorch的网络模块。我们在CustomActivation类的初始化函数init中定义了一个可以训练的参数self.a。这个参数是用nn.Parameter函数从输入的初始化值a_init_value创建的，它会自动添加到模块的参数列表中，所以在优化过程中，优化器会自动更新这个参数。

在CustomActivation类的forward方法中，我们定义了这个自定义激活函数的具体操作。当我们用这个模块处理输入数据时，PyTorch会自动调用这个方法。在这个方法中，我们先用torch.exp函数计算-self.a * x的指数，然后再用1.0 / (1.0 + …)计算出这个自定义激活函数的输出。

接下来，我们定义了一个新的网络层MyLayer。这个网络层有一个线性层self.linear和一个自定义激活函数self.custom_activation。在这个网络层的forward方法中，我们先用线性层处理输入数据，然后再用自定义激活函数处理线性层的输出。

在这段代码的最后部分，我们创建了一个MyLayer的实例my_layer，然后用这个实例处理了一个随机生成的输入数据input_data。我们先用torch.randn函数生成了一个形状为(5, 10)的随机张量，然后把这个张量作为输入数据传递给了my_layer。在这个过程中，PyTorch会自动调用my_layer的forward方法，计算出网络层的输出。

总的来说，这段代码主要展示了如何在PyTorch中自定义一个激活函数，并把这个激活函数用在一个网络层中。在这个过程中，我们用到了PyTorch的Module类、Parameter类、Linear类等关键功能。

在my_layer = MyLayer(10, 20)中，10和20分别是神经网络层（线性层）的输入维度和输出维度。

输入维度10意味着每个输入样本应有10个特征。
输出维度20意味着该层将每个输入样本转换为具有20个特征的输出。
input_data = torch.randn(5, 10)中的5和10分别代表批次大小（batch size）和特征数。其中：

大模型相关知识

RAG

RAG 检索增强生成（Retrieval Augmented Generation），已经成为当前最火热的LLM应用方案。

LLM 面临的已知挑战包括：

• 在没有答案的情况下提供虚假信息
• 当用户需要特定的当前响应时，提供过时或通用的信息。
• 从非权威来源创建响应。
• 由于术语混淆，不同的培训来源使用相同的术语来谈论不同的事情，因此会产生不准确的响应。

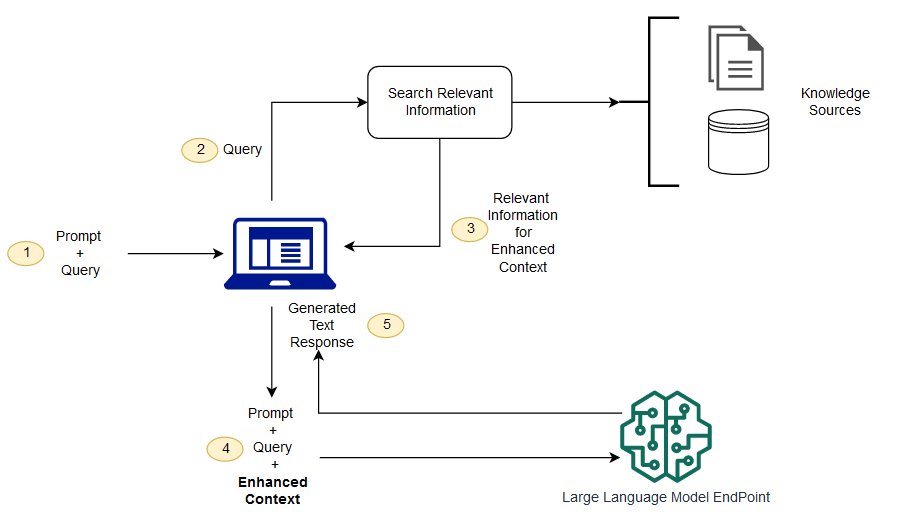
RAG工作原理：

1. 创建外部数据
   LLM 原始训练数据集之外的新数据称为外部数据。它可以来自多个数据来源，例如 API、数据库或文档存储库。数据可能以各种格式存在，例如文件、数据库记录或长篇文本。另一种称为嵌入语言模型的 AI 技术将数据转换为数字表示形式并将其存储在向量数据库中。这个过程会创建一个生成式人工智能模型可以理解的知识库。

2. 检索相关信息
   下一步是执行相关性搜索。用户查询将转换为向量表示形式，并与向量数据库匹配。例如，考虑一个可以回答组织的人力资源问题的智能聊天机器人。如果员工搜索：“我有多少年假？”，系统将检索年假政策文件以及员工个人过去的休假记录。这些特定文件将被退回，因为它们与员工输入的内容高度相关。相关性是使用数学向量计算和表示法计算和建立的。

3. 增强 LLM 提示
   接下来，RAG 模型通过在上下文中添加检索到的相关数据来增强用户输入（或提示）。此步骤使用提示工程技术与 LLM 进行有效沟通。增强提示允许大型语言模型为用户查询生成准确的答案。

4. 更新外部数据

下一个问题可能是——如果外部数据过时了怎么办？ 要维护当前信息以供检索，请异步更新文档并更新文档的嵌入表示形式。您可以通过自动化实时流程或定期批处理来执行此操作。这是数据分析中常见的挑战——可以使用不同的数据科学方法进行变更管理。

检索增强生成和语义搜索有什么区别？

语义搜索可以提高 RAG 结果，适用于想要在其 LLM 应用程序中添加大量外部知识源的组织。现代企业在各种系统中存储大量信息，例如手册、常见问题、研究报告、客户服务指南和人力资源文档存储库等。上下文检索在规模上具有挑战性，因此会降低生成输出质量。

语义搜索技术可以扫描包含不同信息的大型数据库，并更准确地检索数据。例如，他们可以回答诸如 “去年在机械维修上花了多少钱？”之类的问题，方法是将问题映射到相关文档并返回特定文本而不是搜索结果。然后，开发人员可以使用该答案为 LLM 提供更多上下文。

RAG 中的传统或关键字搜索解决方案对知识密集型任务产生的结果有限。开发人员在手动准备数据时还必须处理单词嵌入、文档分块和其他复杂问题。相比之下，语义搜索技术可以完成知识库准备的所有工作，因此开发人员不必这样做。它们还生成语义相关的段落和按相关性排序的标记词，以最大限度地提高 RAG 有效载荷的质量。