dataloader解析
简单例子
总结：对于一般的数据来说，我们把数据量放在第0维，例如[300,3,32,32]。300张3通道，高宽为32的图片。如果batch_size为16，那么每次读取的数据为[300,3,32,32]
假设我们有一个数据集，每个样本都是一个3通道的32x32的图像，标签是一个数字。我们将创建一个自定义的 Dataset 类，然后用 DataLoader 来加载数据，并指定一个 batch_size。我们将打印出从 DataLoader 获取的批次数据的形状。
首先是自定义的 Dataset 类：
from torch.utils.data import Dataset, DataLoader
import torch
class SimpleDataset(Dataset):
def __init__(self, num_samples):
# 假设有 num_samples 个样本，每个样本是3通道的32x32图像
self.data = torch.randn(num_samples, 3, 32, 32)
# 假设每个样本的标签是一个数字
self.labels = torch.randint(0, 10, (num_samples,))
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
sample = self.data[idx]
label = self.labels[idx]
return sample, label然后是使用 DataLoader 来加载数据：
# 创建一个含有100个样本的数据集
simple_dataset = SimpleDataset(num_samples=100)
# 使用DataLoader来加载数据，指定batch_size为4
dataloader = DataLoader(simple_dataset, batch_size=4, shuffle=True)
# 从DataLoader获取第一个批次的数据
for batch_idx, (samples, labels) in enumerate(dataloader):
print(f'Batch index: {batch_idx}')
print('Samples shape:', samples.shape) # 预期形状：[4, 3, 32, 32]
print('Labels shape:', labels.shape) # 预期形状：[4]
break # 只打印第一个批次的数据在这个例子中，samples 的形状应该是 [4, 3, 32, 32]，因为 batch_size 是4，所以有4个样本，每个样本是3通道的32x32图像。labels 的形状应该是 [4]，因为每个批次有4个标签。
dataloader中batch_size,getitem中idx，len之间的关联
首先说一下len函数，返回的是一个数值，一般来说表示的是数据集的长度/多少。
比如我有一个数据集特征和标签：torch.Size([180, 10, 1, 480, 120])
如果len函数：
def __len__(self):
return len(self.features)那么这个长度就是180。
getitem中idx就是和这个长度绑定的。假设长度是180，那么idx的范围就是从0-179这180个数。
batch_size就是用来表示每个数据集的大小，假设batch_size是32，那么这个数据集会被划分为5份，前四份每份有32个，最后一份因为不足32只有20个
前四个batch，每个batch都会调用32次getitem函数，最后一个调用20次；idx会从0开始逐次递增，一直到179。
而在创建dataloader的时候，我们往往可以选择是否打乱
data_loader = DataLoader(dataset=DateSet, batch_size=32, shuffle=False)当数据打乱（shuffle）时，idx实际上指的是打乱后的索引顺序，而不是数据原始顺序的连续索引。也就是说，在每个epoch开始之前，整个数据集的索引会被打乱，然后这个打乱后的索引被用来访问数据集中的样本。
例如原来的数据有：d1,d2,d3,d4,d5,d6,d7
索引为：0,1,2,3,4,5,6
调用的顺序：d1,d2,d3,d4,d5,d6,d7
而数据（索引）打乱后，索引可能为：5,2,3,6,0,1,4
调用的顺序：d6,d3,d4,d7,d1,d2,d5
每次启动一个新的epoch时，如果shuffle=True，则数据会再次被打乱，产生一个新的索引序列。这样做的目的是为了在训练过程中引入随机性，有助于模型泛化，避免对特定的样本顺序过拟合。
Batch
梯度更新机制
深度学习会把数据集划分成多个batch，模型会依次处理每一个Batch。一旦完成某个Batch的反向传播计算出梯度（loss.backward()），优化器会立刻使用这个梯度来更新模型参数（optimizer.step()）。
一般来说多个batch之间的梯度我们不希望累计，所以会调用 optimizer.zero_grad()对梯度清零。
所以一般深度学习训练代码的大致代码如下：
for epoch in range(self.argtrain_epochs):
for i, (batch_x, batch_ybatch_x_mark, batch_y_mark) ienumerate(train_loader):
model_optim.zero_grad()
loss = criterion(outputsbatch_y)
loss.backward()
model_optim.step()
梯度累计
当我们的硬件（如GPU显存）无法容纳大batch size时，我们可以使用梯度累积来模拟大batch的效果。
连续处理多个小batch，但不立即更新模型参数（即不调用 optimizer.step()），并且不清空梯度（即不调用 optimizer.zero_grad()）。这样，梯度会在连续的小batch间进行累加。在处理完N个小batch后，我们再调用一次 optimizer.step()来更新参数，此时优化器使用的是N个小batch累加后的平均梯度效果。
数据相关操作
轴和stack的区别
轴和stack是从两个不同的角度去对数组进行操作
stack涉及hstack和vstack，h是水平，v表示垂直。就是物理直观描述
如果numpy用的是hstack/vstack来进行操作，那么头脑中浮现的是中学的xy坐标轴
一个(2,3)的数组，一共有两行，三列。
如果是下面这种形式生成的数组，那么用axis的方式理解可能更好点
>>> import numpy as np
>>> a = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> a
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])涉及axis的操作，包括concatenate，头脑浮现的应该是下面的坐标系：
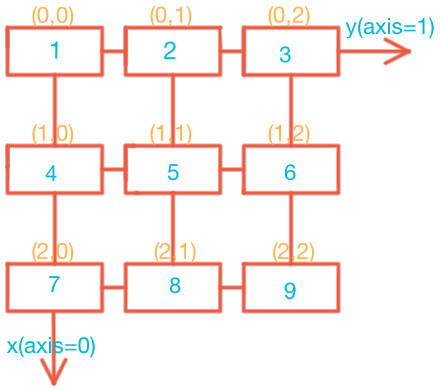
非常的直观。
所以在使用hstack/vstack和axis的时候一定要注意下想象的东西。
轴（axis）
>>> import numpy as np
>>> a = np.array([[1,2,3],[2,3,4],[3,4,9]])
>>> a
array([[1, 2, 3],
[2, 3, 4],
[3, 4, 9]])这个array的维数只有2，即axis轴有两个，分别是axis=0和axis=1。如下图所示，该二维数组的第0维(axis=0)有三个元素(左图)，即axis=0轴的长度length为3；第1维(axis=1)也有三个元素(右图)，即axis=1轴的长度length为3。正是因为axis=0、axis=1的长度都为3，矩阵横着竖着都有3个数，所以该矩阵在线性代数是3维的(rank秩为3)。
因此，axis就是数组层级。
当axis=0，该轴上的元素有3个(数组的size为3)
a[0]、a[1]、a[2]
当axis=1，该轴上的元素有3个(数组的size为3)
a[0][0]、a[0][1]、a[0][2]
（或者a[1][0]、a[1][1]、a[1][2]）
（或者a[2][0]、a[2][1]、a[2][2]）
再比如下面shape为(3,2,4)的array：
>>> b = np.array([[[1,2,3,4],[1,3,4,5]],[[2,4,7,5],[8,4,3,5]],[[2,5,7,3],[1,5,3,7]]])
>>> b
array([[[1, 2, 3, 4],
[1, 3, 4, 5]],
[[2, 4, 7, 5],
[8, 4, 3, 5]],
[[2, 5, 7, 3],
[1, 5, 3, 7]]])
>>> b.shape
(3, 2, 4)这个shape（用tuple表示）可以理解为在每个轴（axis）上的size，也即占有的长度（length)。为了更进一步理解，我们可以暂时把多个axes想象成多层layers。axis=0表示第一层(下图黑色框框)，该层数组的size为3，对应轴上的元素length = 3；axis=1表示第二层(下图红色框框)，该层数组的size为2，对应轴上的元素length = 2；axis=2表示第三层(下图蓝色框框)，对应轴上的元素length = 4。
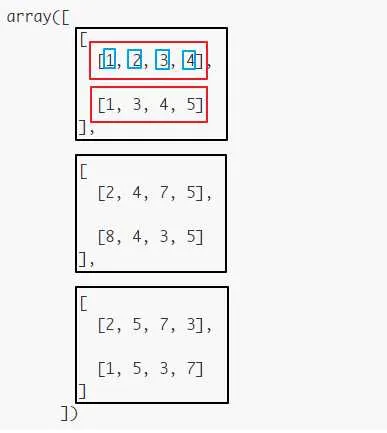
stack
import numpy
a=numpy.arange(1, 7).reshape((2, 3))
b=numpy.arange(7, 13).reshape((2, 3))
c=numpy.arange(13, 19).reshape((2, 3))
d=numpy.arange(19, 25).reshape((2, 3))这四个用于堆叠的数组如下所示：
[[1 2 3]
[4 5 6]]
[[ 7 8 9]
[10 11 12]]
[[13 14 15]
[16 17 18]]
[[19 20 21]
[22 23 24]]
print(numpy.stack([a, b,c,d], axis=0))
print(numpy.stack([a, b,c,d], axis=0).shape)输出结果：
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]
[[13 14 15]
[16 17 18]]
[[19 20 21]
[22 23 24]]]
(4, 2, 3)形象理解：axis等于几就说明在哪个维度上进行堆叠。当axis=0的时候，意味着整体，也就是一个2行3列的数组。所以对于0维堆叠，相当于简单的物理罗列，比如这四个数组代表的是4张图像的数据，进行0维堆叠也就是把它们按顺序排放了起来，形成了一个(4,2,3)的3维数组。
axis=1
print(numpy.stack([a, b,c,d], axis=1))
print(numpy.stack([a, b,c,d], axis=1).shape)输出：
[[[ 1 2 3]
[ 7 8 9]
[13 14 15]
[19 20 21]]
[[ 4 5 6]
[10 11 12]
[16 17 18]
[22 23 24]]]
(2, 4, 3)形象理解：axis等于几就说明在哪个维度上进行堆叠。当axis=1的时候，意味着第一个维度，也就是数组的每一行。所以对于1维堆叠，4个2行3列的数组，各自拿出自己的第一行数据进行堆叠形成3维数组的第一“行”，各自拿出自己的第二行数据进行堆叠形成3维数组的第二“行”，从而形成了一个(2,4,3)的3维数组。比如这四个数组分别代表的是对同一张图像进行不同处理后的数据，进行1维堆叠可以将这些不同处理方式的数据有条理的堆叠形成一个数组，方便后续的统一处理。
axis=2
print(numpy.stack([a, b,c,d], axis=2))
print(numpy.stack([a, b,c,d], axis=2).shape)[[[ 1 7 13 19]
[ 2 8 14 20]
[ 3 9 15 21]]
[[ 4 10 16 22]
[ 5 11 17 23]
[ 6 12 18 24]]]
(2, 3, 4)concatenate
>>> a = np.array([[1, 2], [3, 4]])
>>> b = np.array([[5, 6]])
>>> np.concatenate((a, b), axis=0)
array([[1, 2],
[3, 4],
[5, 6]])
>>> np.concatenate((a, b.T), axis=1)
array([[1, 2, 5],
[3, 4, 6]])torch.Tensor.unfold
Tensor.unfold(dimension, size, step) → Tensor
这个主要是针对tensor的操作，用类似滑动窗口的形式来分割数据。
但是这个操作迷糊了我很长的时间，尤其是二维tensof的时候，半天才明白。
>>> x=torch.randn(7)
>>> x
tensor([-0.4521, -1.4267, -0.1274, 0.7624, -0.0913, -0.3977, -0.7435])
>>> y=x.unfold(0,2,1)
>>> y
tensor([[-0.4521, -1.4267],
[-1.4267, -0.1274],
[-0.1274, 0.7624],
[ 0.7624, -0.0913],
[-0.0913, -0.3977],
[-0.3977, -0.7435]])
>>> y.shape
torch.Size([6, 2])
>>> z=y.unfold(0,2,2)
>>> z
tensor([[[-0.4521, -1.4267],
[-1.4267, -0.1274]],
[[-0.1274, 0.7624],
[ 0.7624, -0.0913]],
[[-0.0913, -0.3977],
[-0.3977, -0.7435]]])
>>> z.shape
torch.Size([3, 2, 2])unfold会在指定的dim上面进行展开，最终会增加一个新的维度。指定dim维度上的数值会变为窗口数量，而增加一个新的维度放到张量末尾，这个维度大小就是窗口大小。
假设一个张量操作为：(6,2)unfold(0,2,2)
窗口大小为2，窗口数量为3，那么新得到的张量shape为([3, 2, 2])
同理
x = torch.randn(3, 5, 7)
y = x.unfold(1, 3, 2)
# torch.Size([3, 2, 7, 3])来放置每个窗口内的数据。这个新维度会被添加到张量的末尾
pytorch中图像分割
简单版：reshape比view更加好用
[原文链接]（https://blog.csdn.net/Flag_ing/article/details/109129752）
我们以实际的代码来看下：
# 输入的是一个5维数组，我要切割为80*20的小块
batch_size, seq_length, channels, h, w = data.shape
# n_h*n_w就是切割后的小块总数
n_h = h // patch_h
n_w = w // patch_w
# 对原来的tensor形状进行变化
images = images.view(batch_size, seq_length, channels, n_h, patch_h, n_w, patch_w)
# 变化后进行重排序，原来是（0,1,2,3,4,5,6），变换后就是（batch_size, seq_length, channels，n_h， n_w， patch_h， patch_w）;再用reshape重构
images.permute(0,1,2,3,5,4,6).reshape(batch_size, seq_length, channels, n_h*n_w, patch_h, patch_w)查看数据结构的维度的维度
tensor:
>>>a = torch.randn(2,2)
>>>a.shape # 使用shape查看Tensor维度
torch.Size([2,2])
>>>a.size() # 使用size()函数查看Tensor维度
torch.Size([2,2])数组或list:
>>>import numpy as np
>>>x = [[[1,2,3],[4,5,6]],[[7,8,9],[0,1,2]],[[3,4,5],[6,7,8]]]
>>>np.array(x).shape
>>>print(x.shape)
(3, 2, 3)TensorDataset与DataLoader的使用
TensorDataset是个只用来存放tensor(张量)的数据集，而DataLoader是一个数据加载器，一般用到DataLoader的时候就说明需要遍历和操作数据了。TensorDataset(tensor1,tensor2)的功能就是形成数据(特征)tensor1和标签tensor2的对应，也就是说tensor1中是数据，而tensor2是tensor1所对应的标签。需要注意的是，tensor1和tensor2的最高维数要相同。比如下面这个例子，tensor1.shape(12,3); tensor2.shape(12)
来个小例子:
from torch.utils.data import TensorDataset,DataLoader
import torch
a = torch.tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
b = torch.tensor([44, 55, 66, 44, 55, 66, 44, 55, 66, 44, 55, 66])
train_ids = TensorDataset(a,b)
# 切片输出
print(train_ids[0:4]) # 第0,1,2,3行
# 循环取数据
for x_train,y_label in train_ids:
print(x_train,y_label)下面是对应的输出:
(tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[1, 2, 3]]), tensor([44, 55, 66, 44]))
===============================================
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)
tensor([1, 2, 3]) tensor(44)
tensor([4, 5, 6]) tensor(55)
tensor([7, 8, 9]) tensor(66)从输出结果我们就可以很好的理解，tensor型数据和tensor型标签的对应了，这就是TensorDataset的基本应用。接下来我们把构造好的TensorDataset封装到DataLoader来操作里面的数据:
# 参数说明，dataset=train_ids表示需要封装的数据集，batch_size表示一次取几个
# shuffle表示乱序取数据，设为False表示顺序取数据，True表示乱序取数据
train_loader = DataLoader(dataset=train_ids,batch_size=4,shuffle=False)
# 注意enumerate返回值有两个,一个是序号，一个是数据（包含训练数据和标签）
# enumerate里面可以不要1，直接写train_loader
# format里面也可以写为i
for i,data in enumerate(train_loader,1):
train_data, label = data
print(' batch:{0} train_data:{1} label: {2}'.format(i+1, train_data, label))下面是输出：
batch:1 x_data:tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[1, 2, 3]]) label: tensor([44, 55, 66, 44])
batch:2 x_data:tensor([[4, 5, 6],
[7, 8, 9],
[1, 2, 3],
[4, 5, 6]]) label: tensor([55, 66, 44, 55])
batch:3 x_data:tensor([[7, 8, 9],
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]) label: tensor([66, 44, 55, 66])numpy.transpose()—坐标轴转换
举个例子，假设x是一个二维数组，那么
没有变化
```x.transpose((1,0))
把1轴的数据和0轴数据进行了交换
x 为：
array([[0, 1],
[2, 3]])我们不妨设第一个方括号“[]”为 0轴 ，第二个方括号为 1轴 ，则x可在 0-1坐标系 下表示如下：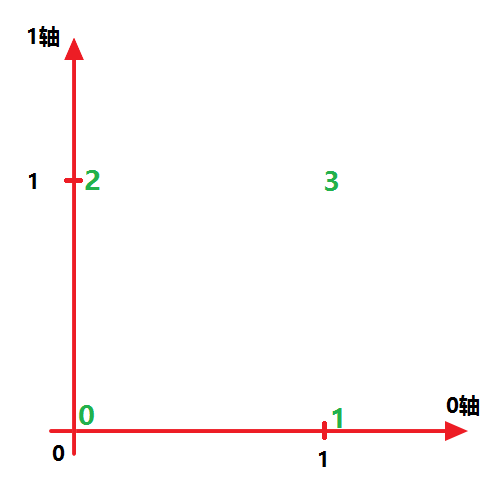
因为 x.transpose((0,1)) 表示按照原坐标轴改变序列，也就是保持不变
而 x.transpose((1,0)) 表示交换 ‘0轴’ 和 ‘1轴’，所以就得到如下图所示结果：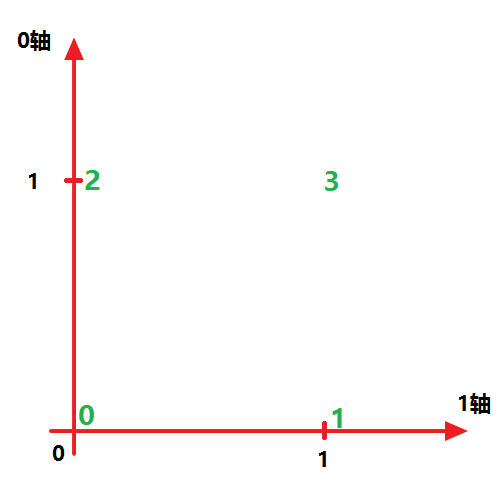
x[0][0] == 0
x[0][1] == 2
x[1][0] == 1
x[1][1] == 3x 转置了
array([[0, 2],
[1, 3]])注意，任何时候你都要保持清醒，告诉自己第一个方括号“[]”为 0轴 ，第二个方括号为 1轴
此时，transpose转换关系就清晰了。
numpy复制并扩充维度
a的shape从（96，96）变成（1000，96，96）
np.expand_dims(a,0).repeat(1000,axis=0)解释：
expand_dims表示增加一个维度，这个维度增加在a的0维度。repeat代表重复的次数，axis代表在哪个维度进行重复。
可以根据自己的需要更改参数。
loss可视化
有时候我们想观察模型训练时候的loss，可以使用tesorboard。这里举个例子
from torch.utils.tensorboard import SummaryWriter
//将数据保存到指定的文件夹。这里注意下，一般是在代码根目录下面的./run/*。例如/run/202307230293
tb = SummaryWriter(run_dir)
//第一个参数是名称，第二个参数是y值，第三个参数是x值。(用x,y画图)
tb.add_scalar('TranLoss', loss_aver, epoch)
tb.add_scalar('ValidLoss', loss_aver, epoch)我们在run目录下面执行如下命令
tensorboard --logdir=./202307230293
//或者下面这个
tensorboard --logdir=./202307230293 --port 8123如果不指定端口，那么默认是6006
但是我们的代码是在内网跑的，很有可能只开放了22端口，本地浏览器通过 ip:端口 是没法访问的，考虑到安全性，是没法开其他端口，只有把端口映射出来
这里以mobaxterm为例，xshell也可以[原链接](https://blog.csdn.net/qq_40944311/article/detail
s/121396856)
- 在Tools中打开MobaSSHTunnel(port forwarding)
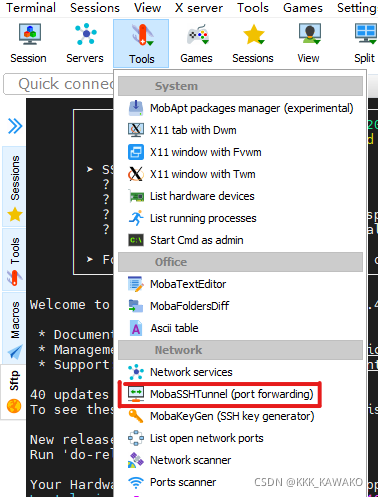
- 点击New SSH tunnel
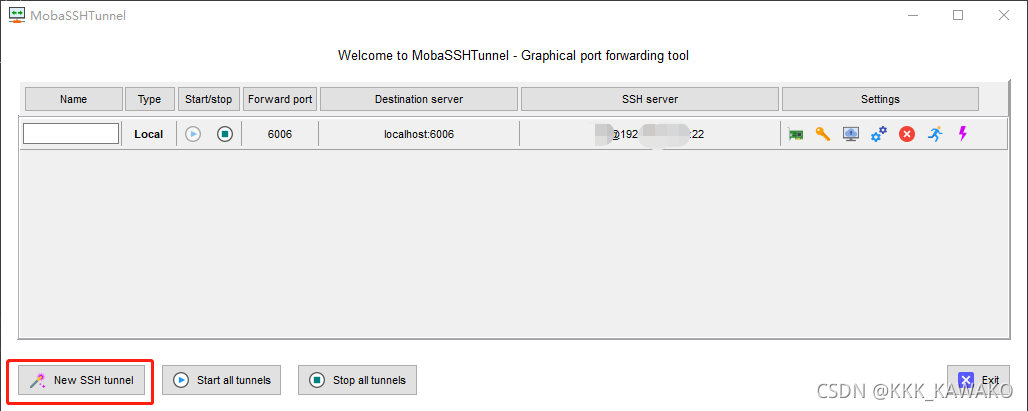
- 配置信息
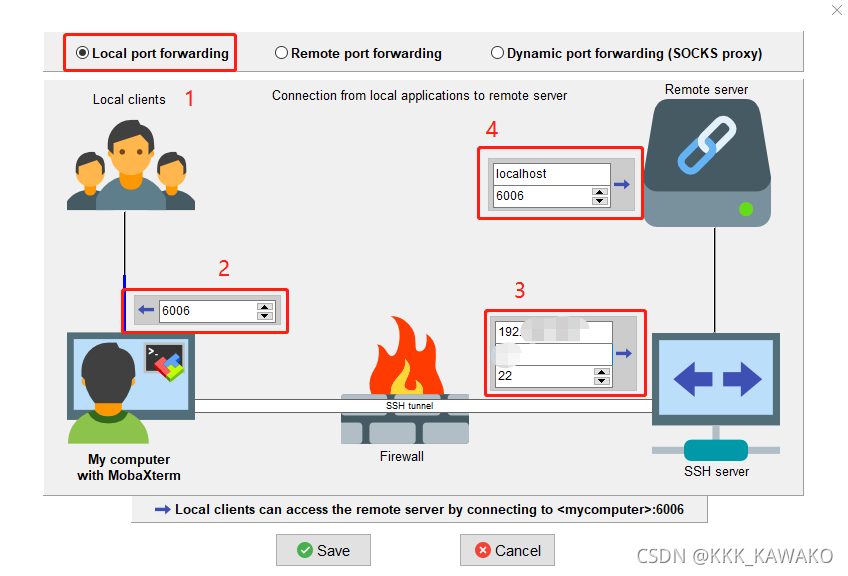
1、选择第一个Local port forwarding
2、输入想要映射到本地的端口号
3、输入远程连接的信息，ip、用户名、ssh端口号22
4、输入服务器端被映射的端口信息
- 点击运行
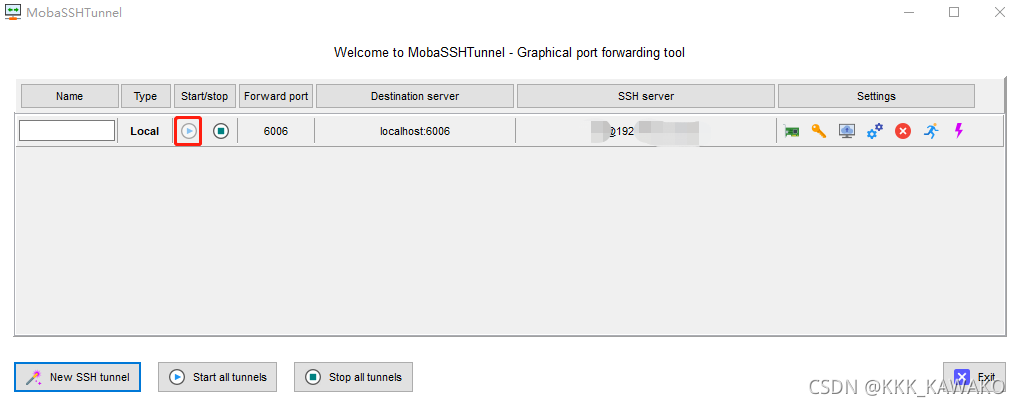
- 访问端口
在服务器上run目录下输入tensorboard --logdir=./202307230293
在本地浏览器输入 localhost:6006
随机种子
随机种子概念
random.seed()函数使用给定值初始化随机数生成器。
种子被赋予一个整数值，以确保伪随机生成的结果是可重现的。
每次生成的随机数序列将是确定性的，这意味着可以在不同的运行中获得相同的随机数序列，从而使实验可复现。
在Python中，随机种子是通过random.seed()函数设置的，而在PyTorch中，可以通过设置torch.manual_seed()来实现，在TensorFlow中，使用tf.random.set_seed()设置。
随机种子与shuff的联系
当我们设置 DataLoader的 shuffle=True时，每个训练周期（epoch）开始前，数据加载器都会使用随机数来打乱数据的顺序。数据打乱并非直接在原始数据集上进行，而是生成一个随机的索引序列。DataLoader会根据这个新的索引顺序来提取数据，组装成批次。
固定随机种子带来的效果是：
- 多次实验间，每个epoch的数据顺序可重现：如果你设置了一个固定的随机种子（比如 42），那么每次你从头运行整个训练脚本时：
- 第1个epoch的数据打乱顺序将是完全相同的。
- 第2个epoch的数据打乱顺序也将是完全相同的。
- 以此类推，每个epoch的数据顺序在多次实验中都保持一致。
随机种子和shuff结合的示例代码：
import torch
import random
import numpy as np
from torch.utils.data import Dataset, DataLoader
# 设置随机种子的函数，确保可复现性
def set_seed(seed):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # 多GPU情况
torch.backends.cudnn.deterministic = True # 禁用非确定性算法
torch.backends.cudnn.benchmark = False
# 设置全局随机种子（例如42）
seed = 42
set_seed(seed)
# 设置随机种子
torch.manual_seed(123)
# 创建一个简单的自定义数据集
class SimpleDataset(Dataset):
def __init__(self):
self.data = [i for i in range(10)] # 数据：0到9的列表
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
# 创建数据集实例
dataset = SimpleDataset()
# 创建DataLoader，设置shuffle=True
# 注意：num_workers=0 避免多进程复杂性（如需多进程需额外设置worker_init_fn）
dataloader = DataLoader(
dataset,
batch_size=2, # 每个batch包含2个样本
shuffle=True, # 关键：启用打乱
num_workers=0 # 单进程简化示例
)
# 运行3个epoch，打印每个epoch的batch数据
num_epochs = 3
for epoch in range(num_epochs):
print(f"--- Epoch {epoch+1} ---")
for batch_idx, batch_data in enumerate(dataloader):
print(f"Batch {batch_idx}: {batch_data}")
print() # 空行分隔epoch是否使用shuff的示例代码：
from torch.utils.data import DataLoader, Dataset
# 一个简单的数据集，包含数字0到9
class SimpleDataset(Dataset):
def __init__(self):
self.data = [i for i in range(10)]
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
return self.data[idx]
dataset = SimpleDataset()
print("=== Shuffle=True ===")
loader_shuffle = DataLoader(dataset, batch_size=2, shuffle=True)
for epoch in range(2): # 模拟2个epoch
print(f"Epoch {epoch+1}: ", end="")
for batch in loader_shuffle:
print(batch, end=" ")
print() # 换行
print("\n=== Shuffle=False ===")
loader_no_shuffle = DataLoader(dataset, batch_size=2, shuffle=False)
for epoch in range(2):
print(f"Epoch {epoch+1}: ", end="")
for batch in loader_no_shuffle:
print(batch, end=" ")
print() # 换行
