快慢指针
力扣876:
快慢指针:比较经典的做法是:
使用两个指针变量,刚开始都位于链表的第 1 个结点,一个永远一次只走 1 步,一个永远一次只走 2 步,一个在前,一个在后,同时走。这样当快指针走完的时候,慢指针就来到了链表的中间位置。
不一定同时从起点一起走,也有可能快指针先走基本,在按照相同补发或不同步伐一起走。
根据这种确定性去解决链表中的一些问题。使用这种思想还可以解决链表的以下问题:
「力扣」第 19 题: 倒数第 k 个结点,快指针先走几步,不是靠猜的,要在纸上画图模拟一下,就清楚了;
「力扣」第 141 题:环形链表,在环中的时候可以想象,A 同学开始有存款 100 元,每天赚 1 元,B 同学开始有存款 50 元,每天赚 2 元,B 同学一定会在某一天和 A 同学的存款一样;
「力扣」第 142 题:环形链表 II;
「力扣」第 161 题:相交链表,起点不同,构造相同长度让它们相遇,同样是利用了同步走这个等量关系。动态规划解题框架
框架:
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)股票问题
重点看一下最大交易次数k
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 今天选择 rest, 今天选择 sell )
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 今天选择 rest, 今天选择 buy )只有从状态0到1,k才会变化。就是从未持有到持有
回溯(两种形式)与动态规划
动态规划一般有两种形式:自顶向下和自底向上
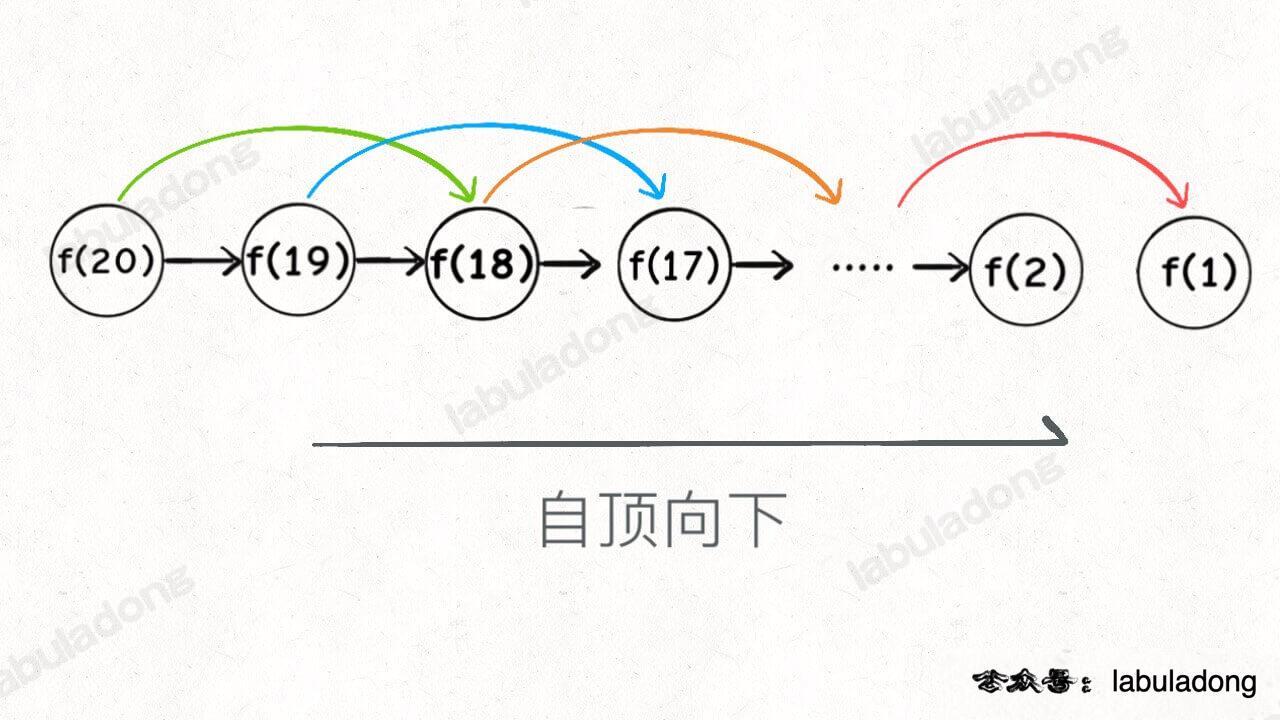
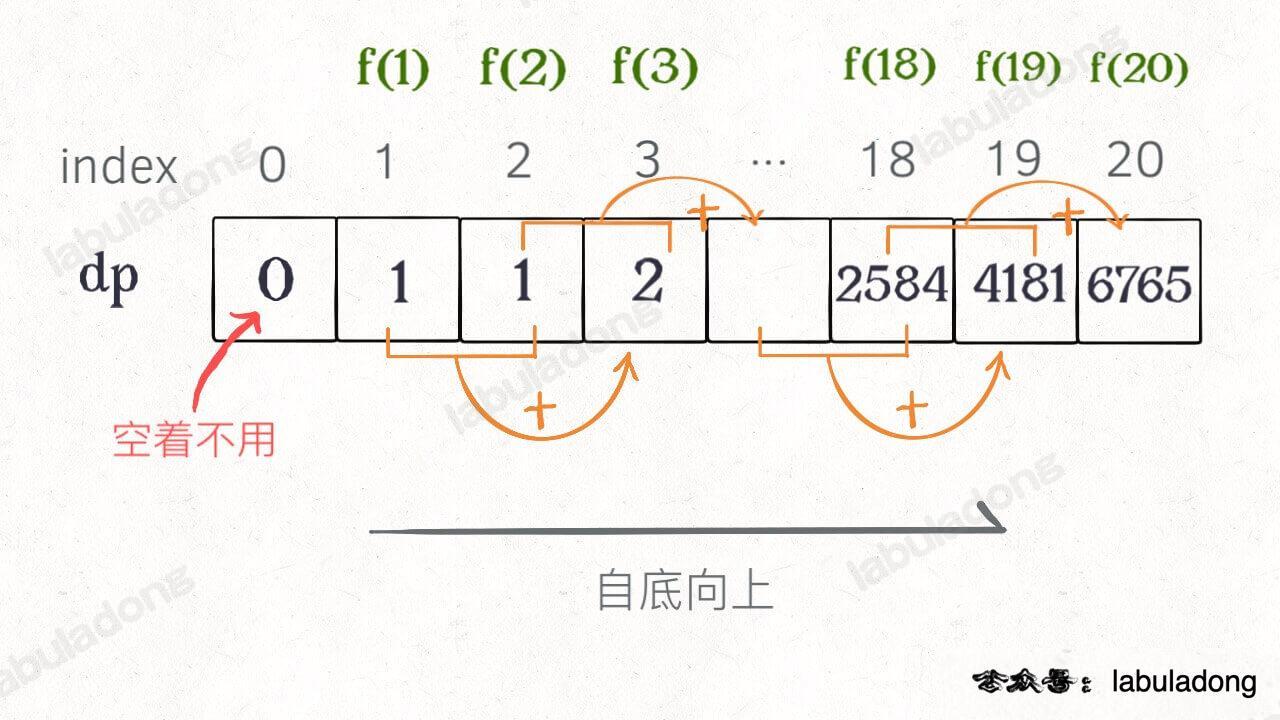
不用管细节,回溯/递归是树,动态规划是数组。
结论:
- 自顶向下就是回溯函数,自底向上就是dp数组。
- 回溯需要单独的一个回溯函数,可以是void类型,也可以是非void类型;如果要使用备忘录优化,需要使用非void类型
- 有的题没法用备忘录,二叉树最大深度就不行。备忘录是记录后面会用到的结果,这个题记了也没有。
- 自底向上就不需要额外的函数,就是dp数组
- dp函数变化的是函数的形参数值,dp数组变化的是索引
两种形式的dp函数(买卖股票题目)
带备忘录写法:
class Solution {
public int maxProfit(int[] prices) {
if(prices==null || prices.length==0) {
return 0;
}
Map<Pair,Integer> map = new HashMap<Pair,Integer>();
return dfs(map,prices,0,false);
}
private int dfs(Map<Pair,Integer> map,int[] prices,int index,boolean status) {
//Pair对象封装了index和status,作为map的key
Pair p = new Pair(index,status);
if(map.containsKey(p)) {
return map.get(p);
}
if(index==prices.length) {
map.put(p,0);
return 0;
}
int a=0,b=0,c=0;
a = dfs(map,prices,index+1,status);
if(status) {
b = dfs(map,prices,index+1,false)+prices[index];
} else {
c = dfs(map,prices,index+1,true)-prices[index];
}
map.put(p,Math.max(Math.max(a,b),c));
return map.get(p);
}
//自定义一个Pair类,封装 index和status
private class Pair {
private final int index;
private final boolean status;
Pair(int index,boolean status) {
this.index = index;
this.status = status;
}
//这里需要实现自定义的equals和hashCode函数
public boolean equals(Object obj) {
Pair other = (Pair)obj;
if(other.index!=this.index) {
return false;
}
if(other.status!=this.status) {
return false;
}
return true;
}
public int hashCode() {
if(this.status) {
return this.index+1;
} else {
return this.index+0;
}
}
}
}备忘录回溯与dp数组
递归
原链接
Rules Number One,基本上,所有的递归问题都可以用递推公式来表示。有了这个递推公式,我们就可以很轻松地将它改为递归代码。。所以,遇到递归不要怕,先想递推公式。
例1: (比较明显的能递推公式的问题)
- 问题:斐波那契数列的第n项
- 递推公式:
f(n)=f(n-1)+f(n-2) 其中,f(0)=0,f(1)=1- 终止条件:
if (n <= 2) return 1;- 递归代码:
int f(int n) {
if (n <= 2) return 1;
return f(n-1) + f(n-2);
}例2:(不那么明显的有递推公式的问题)
- 问题:逆序打印一个数组
- 递推公式:
假设令F(n)=逆序遍历长度为n的数组
那么F(n)= 打印数组中下标为n的元素 + F(n-1)- 终止条件:
if (n <0) return ;- 递归代码:
public void Print(int[] nums,int n){
if(n<0) return;
System.out.println(nums[n]);
Print(nums,n-1);
}到这里,不知道大家对写递归有没有一些理解了。其实写递归不能总想着去把递归平铺展开,这样脑子里就会循环,一层一层往下调,然后再一层一层返回,试图想搞清楚计算机每一步都是怎么执行的,这样就很容易被绕进去。对于递归代码,这种试图想清楚整个递和归过程的做法,实际上是进入了一个思维误区。只要找到递推公式,我们就能很轻松地写出递归代码。
到这里,我想进一步跟大家说明我这个思路是比较能够容易出代码的,那么就树的遍历问题来和大家讲。递归总是和树分不开,其中,最典型的便是树的遍历问题。刚开始学的时候,不知道大家是怎么理解先/中/后序遍历的递归写法的,这里我提供我的思路供参考,以前序遍历为例:
- 问题:二叉树的先序遍历
- 递推公式:
令F(Root)为问题:遍历以Root为根节点的二叉树,
令F(Root.left)为问题:遍历以F(Root.left)为根节点的二叉树
令F(Root.right)为问题:遍历以F(Root.right)为根节点的二叉树
那么其递推公式为:
F(Root)=遍历Root节点+F(Root.left)+F(Root.right)- 递归代码:
public void preOrder(TreeNode node){
if(node==null) return;
System.out.println(node.val);
preOrder(node.left);
preOrder(node.righr);
}Rules Number Two, 递归是一种关于某个重复动作(完成重复性的功能)的形式化描述。具体点讲,如果一个问题 A 可以分解为若干子问题 B、C、D,你可以假设子问题 B、C、D 已经解决,在此基础上思考如何解决问题 A。而且,你只需要思考问题 A 与子问题 B、C、D 两层之间的关系即可,不需要一层一层往下思考子问题与子子问题,子子问题与子子子问题之间的关系(也就是说,递归只能考虑当前层和下一层的关系,不能继续往下深入)。我们需要屏蔽掉递归细节,理解为完成了某种功能的形式化描述即可。
- 问题:单向链表的反转
- 递推公式
令F(node)为问题:反转以node为头节点的单向链表;
一般,我们需要考虑F(n)和F(n-1)的关系,那么这里,如果n代表以node为头节点的单向链表,那么n-1就代表以node.next为头节点的单向链表.
所以,我们令F(node.next)为问题:反转以node.next为头节点的单向链表;
那么,F(node)和F(node.next)之间的关系是?这里我们来简单画个图,假设我们反转3个节点的链表:
1 -> 2 -> 3
那么,F(node=1)=F(node=2)+?
这里假设子问题F(node=2)已经解决,那么我们如何解决F(node=1):
很明显,我们需要反转node=2和node=1, 即 node.next.next=node; 同时 node.next=null;
所以,这个问题就可以是:F(node=1)=F(node=2)+ 反转node=2和node=1- 递归代码:
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null) { //终止条件并不难想
return head;
}
ListNode node = reverseList(head.next);
head.next.next = head;
head.next = null;
return node; //按上面的例子,F(node=1)和F(node=2)它俩反转后的头节点是同一个
}3.写递归的小tips
- 将问题抽象化,可以将问题抽象为f(n)(或者其他的数学符号),
然后用f(n)代表欲求的问题,然后去发现和子问题(比如f(n-1))的递推关系!(这一点在写动态规划的时候特别有用,其实动态规划就是记忆化的递归!) - 递归函数是带语义的,但是记住一个递归函数只有一个语义,如果在写递归函数实现的时候,发现出现了多个语义,需要对新出现的语义重新定义一个函数!
- 在写递归函数的时候,可以先写子问题f(n-1),再写所求问题f(n),这样的话就很好知道f(n)和f(n-1)的关系,更容易保证一个递归函数只包含一个语义。
求数组所有子数组的方法
一个包含n个元素的集合,求它的所有子集。比如集合A= {1,2,3}, 它的所有子集是:
{ {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, @}(@表示空集)。
这种问题一般有两种思路,先说说第一种,递归。递归肯定要基于一个归纳法的思想,这个思想用到了二叉树的遍历,如下图所示:
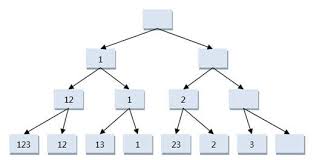
可以这样理解这张图,从集合A的每个元素自身分析,它只有两种状态,或是某个子集的元素,或是不属于任何子集,所以求子集的过程就可以看成对每个元素进行“取舍”的过程。上图中,根结点是初始状态,叶子结点是终结状态,该状态下的8个叶子结点就表示集合A的8个子集。第i层(i=1,2,3…n)表示已对前面i-1层做了取舍,所以这里可以用递归了。整个过程其实就是对二叉树的先序遍历。
代码见方法getSonSet1。
还有一种思想比较巧妙,可以叫按位对应法。如集合A={a,b,c},对于任意一个元素,在每个子集中,要么存在,要么不存在。
映射为子集:
(a,b,c)
(1,1,1)->(a,b,c)
(1,1,0)->(a,b)
(1,0,1)->(a,c)
(1,0,0)->(a)
(0,1,1)->(b,c)
(0,1,0)->(b)
(0,0,1)->©
(0,0,0)->@(@表示空集)
观察以上规律,与计算机中数据存储方式相似,故可以通过一个整型数与集合映射00…00 ~ 11…11(1表示有,0表示无,反之亦可),通过该整型数逐次增可遍历获取所有的数,即获取集合的相应子集。
实现代码见方法getSonSet2
import java.util.ArrayList;
import java.util.List;
public class SonSet {
public static void main(String[] args){
int[] arr={1,2,3};
List<Integer> aList=new ArrayList<Integer>();
List<Integer> bList=new ArrayList<Integer>();
for(int i=0;i<arr.length;i++){
aList.add(arr[i]);
}
getSonSet1(0,aList,bList); //方法1,递归法
System.out.println("----数组arr公用,分割线-----");
getSonSet2(arr,arr.length); //方法2,按位对应法
}
/*
* 递归法
*/
public static void getSonSet1(int i,List<Integer> aList,List<Integer> bList){
if(i>aList.size()-1){
if(bList.size()<=0){
System.out.print("@");
}else {
/*for(int v:bList){
System.out.print(v+",");//可以直接用这种方法输出bList数组里所有值,但是每个子数组最后就会带逗号
}*/
System.out.print(bList.get(0));
for(int m=1;m<bList.size();m++){
System.out.print(","+bList.get(m));
}
}
System.out.println();
}else {
bList.add(aList.get(i));
getSonSet1(i+1, aList, bList);
int bLen=bList.size();
bList.remove(bLen-1);
getSonSet1(i+1, aList, bList);
}
}
/*
*按位对应法。
*/
private static void getSonSet2(int[] arr, int length) {
int mark=0;
int nEnd=1<<length;
boolean bNullSet=false;
for(mark=0;mark<nEnd;mark++){
bNullSet=true;
for(int i=0;i<length;i++){
if(((1<<i)&mark)!=0){//该位有元素输出
bNullSet=false;
System.out.print(arr[i]+",");
}
}
if(bNullSet){//空集合
System.out.print("@");
}
System.out.println();
}
}
}
运行结果:
1,2,3
1,2
1,3
1
2,3
2
3
@
----数组arr公用,分割线-----
@
1,
2,
1,2,
3,
1,3,
2,3,
1,2,3,
排序
冒泡
原始
//按照刚才那个动图进行对应
//冒泡排序两两比较的元素是没有被排序过的元素--->
public void bubbleSort(int[] array){
for(int i=0;i<array.length-1;i++){//控制比较轮次,一共 n-1 趟
for(int j=0;j<array.length-1-i;j++){//控制两个挨着的元素进行比较
if(array[j] > array[j+1]){
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
}
优化
public static int[] bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return arr;
}
for (int i = 0; i < arr.length - 1; i++) {
boolean isSorted = true;//有序标记,每一轮的初始是true
for (int j = 0; j < arr.length -i - 1; j++) {
if (arr[j + 1] < arr[j]) {
isSorted = false;//有元素交换,所以不是有序,标记变为false
int t = arr[j];
arr[j] = arr[j+1];
arr[j+1] = t;
}
}
//一趟下来是否发生位置交换,如果没有交换直接跳出大循环
if(isSorted )
break;
}
return arr;
}
岛屿类问题的通用解法、DFS 遍历框架
原文链接
我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
本文将以岛屿问题为例,展示网格类问题 DFS 通用思路,以及如何让代码变得简洁。
网格问题的基本概念
我们首先明确一下岛屿问题中的网格结构是如何定义的,以方便我们后面的讨论。
网格问题是由 m \times nm×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子,数字为 1 的格子看成陆地格子,这样相邻的陆地格子就连接成一个岛屿。
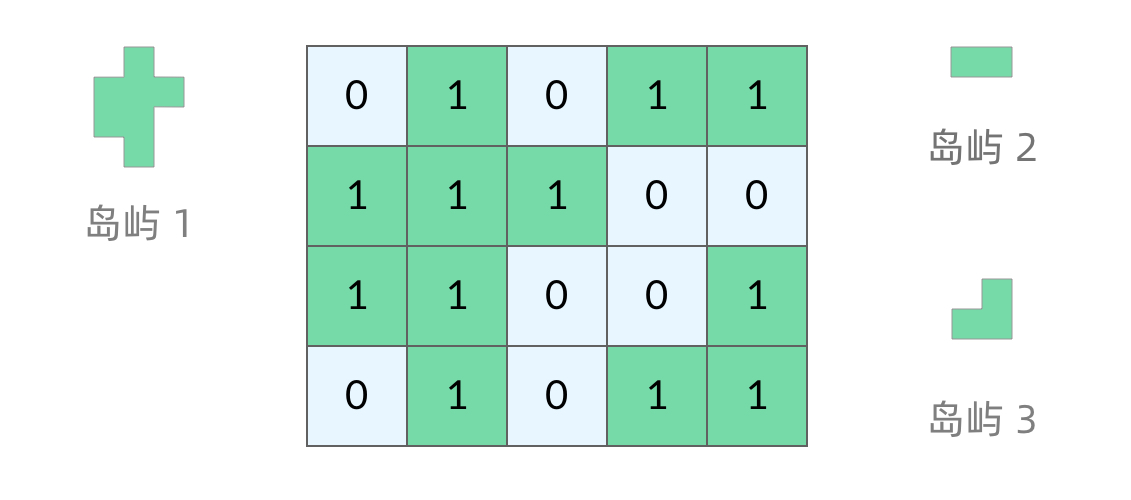
在这样一个设定下,就出现了各种岛屿问题的变种,包括岛屿的数量、面积、周长等。不过这些问题,基本都可以用 DFS 遍历来解决。
DFS 的基本结构
网格结构要比二叉树结构稍微复杂一些,它其实是一种简化版的图结构。要写好网格上的 DFS 遍历,我们首先要理解二叉树上的 DFS 遍历方法,再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的:
void traverse(TreeNode root) {
// 判断 base case
if (root == null) {
return;
}
// 访问两个相邻结点:左子结点、右子结点
traverse(root.left);
traverse(root.right);
}可以看到,二叉树的 DFS 有两个要素:「访问相邻结点」和「判断 base case」。
第一个要素是访问相邻结点。二叉树的相邻结点非常简单,只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构:一棵二叉树,它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。
第二个要素是 判断 base case。一般来说,二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义:一方面,这表示 root 指向的子树为空,不需要再往下遍历了。另一方面,在 root == null 的时候及时返回,可以让后面的 root.left 和 root.right 操作不会出现空指针异常。
对于网格上的 DFS,我们完全可以参考二叉树的 DFS,写出网格 DFS 的两个要素:
首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。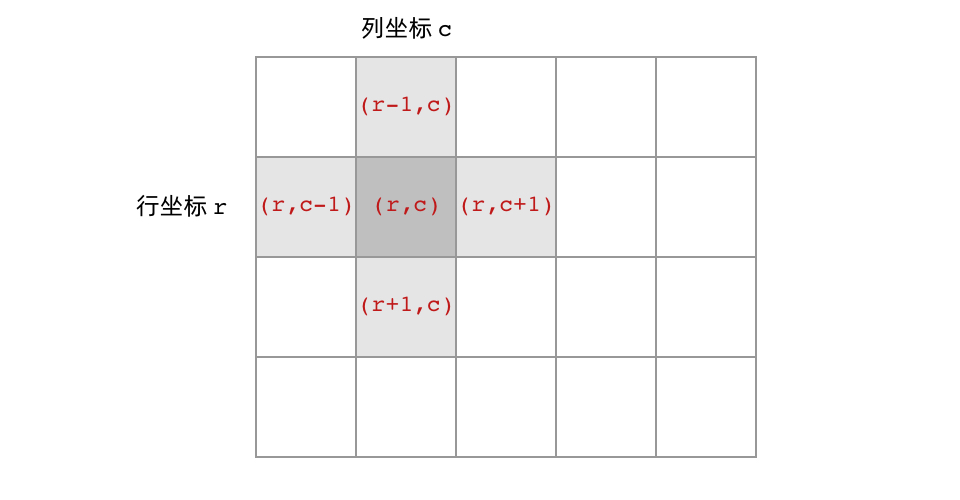
其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。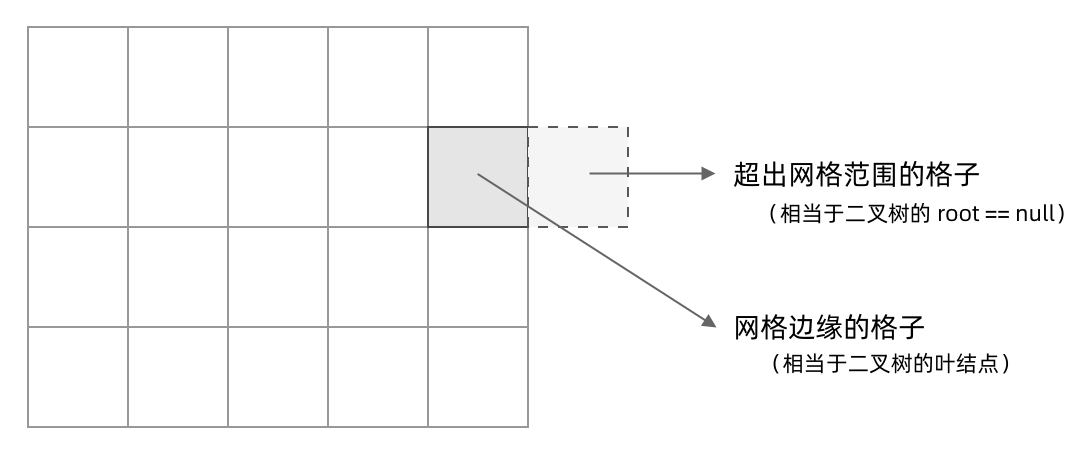
这一点稍微有些反直觉,坐标竟然可以临时超出网格的范围?这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子,先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的,先递归调用,发现 root == null 再返回。
这样,我们得到了网格 DFS 遍历的框架代码:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
// 如果坐标 (r, c) 超出了网格范围,直接返回
if (!inArea(grid, r, c)) {
return;
}
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}如何避免重复遍历
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。
如何避免这样的重复遍历呢?答案是标记已经遍历过的格子。以岛屿问题为例,我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子,就把格子的值改为 2,这样当我们遇到 2 的时候,就知道这是遍历过的格子了。也就是说,每个格子可能取三个值:
0 —— 海洋格子
1 —— 陆地格子(未遍历过)
2 —— 陆地格子(已遍历过)
我们在框架代码中加入避免重复遍历的语句:
void dfs(int[][] grid, int r, int c) {
// 判断 base case
if (!inArea(grid, r, c)) {
return;
}
// 如果这个格子不是岛屿,直接返回
if (grid[r][c] != 1) {
return;
}
grid[r][c] = 2; // 将格子标记为「已遍历过」
// 访问上、下、左、右四个相邻结点
dfs(grid, r - 1, c);
dfs(grid, r + 1, c);
dfs(grid, r, c - 1);
dfs(grid, r, c + 1);
}
// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
return 0 <= r && r < grid.length
&& 0 <= c && c < grid[0].length;
}BFS
二叉树BFS
public void levelOrder(TreeNode tree) {
if (tree == null)
return;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(tree);//相当于把数据加入到队列尾部
while (!queue.isEmpty()) {
//poll方法相当于移除队列头部的元素
TreeNode node = queue.poll();
System.out.println(node.val);
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}leetcode 116
public Node connect(Node root) {
if (root == null)
return root;
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
//每一层的数量
int levelCount = queue.size();
//前一个节点
Node pre = null;
for (int i = 0; i < levelCount; i++) {
//出队
Node node = queue.poll();
//如果pre为空就表示node节点是这一行的第一个,
//没有前一个节点指向他,否则就让前一个节点指向他
if (pre != null) {
pre.next = node;
}
//然后再让当前节点成为前一个节点
pre = node;
//左右子节点如果不为空就入队
if (node.left != null)
queue.add(node.left);
if (node.right != null)
queue.add(node.right);
}
}
return root;
}优化版本:
上面运行效率并不是很高,这是因为我们把节点不同的入队然后再不停的出队,其实可以不需要队列,每一行都可以看成一个链表比如第一行就是只有一个节点的链表,第二行是只有两个节点的链表(假如根节点的左右两个子节点都不为空)……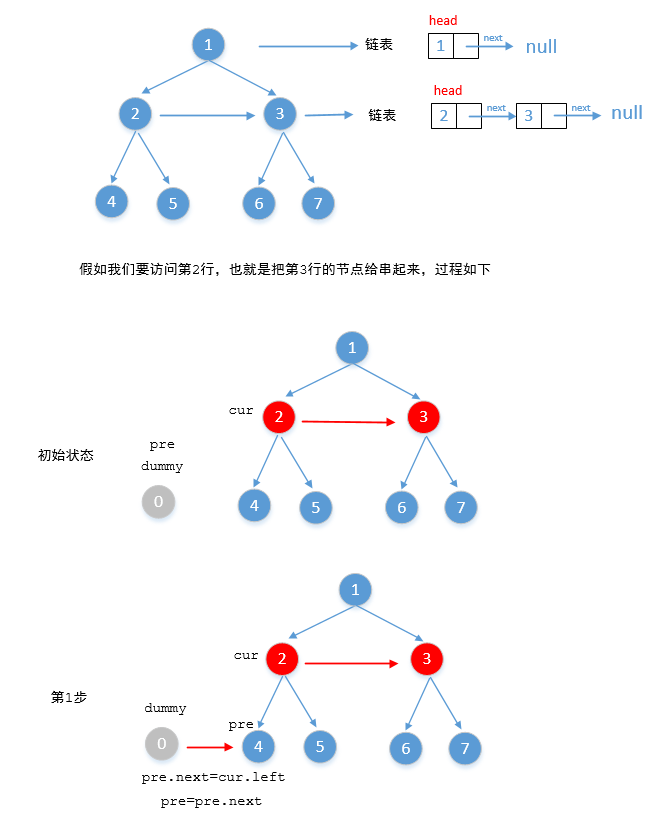
public Node connect(Node root) {
if (root == null)
return root;
//cur我们可以把它看做是每一层的链表
Node cur = root;
while (cur != null) {
//遍历当前层的时候,为了方便操作在下一
//层前面添加一个哑结点(注意这里是访问
//当前层的节点,然后把下一层的节点串起来)
Node dummy = new Node(0);
//pre表示下一层节点的前一个节点
Node pre = dummy;
//然后开始遍历当前层的链表
//因为是完美二叉树,如果有左子节点就一定有右子节点
while (cur != null && cur.left != null) {
//让pre节点的next指向当前节点的左子节点,也就是把它串起来
pre.next = cur.left;
//然后再更新pre
pre = pre.next;
//pre节点的next指向当前节点的右子节点,
pre.next = cur.right;
pre = pre.next;
//继续访问这一行的下一个节点
cur = cur.next;
}
//把下一层串联成一个链表之后,让他赋值给cur,
//后续继续循环,直到cur为空为止
cur = dummy.next;
}
return root;
}


