位置编码

背景

位置编码主要是解决注意力机制中的permutation invarient（置换不变）带来的问题。为了弄清楚位置编码，需要先补充一些背景知识

permutation invarient

置换不变：随意调换输入中词的位置，并不会让注意力权重发生变化，注意力层的整个结果维持不变。具体来说，每一个词向量计算结果不变，仅仅是词向量在输出矩阵的排列随着词和词位置互换而对应调整了一下。词向量输出矩阵可参考下图：

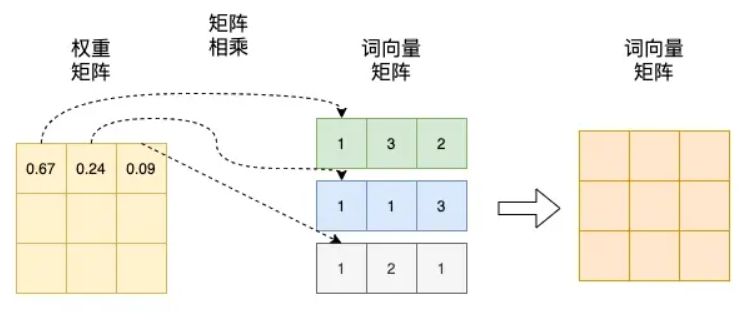
这样会带来一个问题，给定同一组（多集）源词向量，不论它们在输入里怎么排，模型（不含位置信息）对它们的整体作用是一样的，输出结果是确定的。比如一个翻译任务，翻译“猫坐在垫子上”和翻译“垫子坐在猫上面”，不加位置编码，输出的结果是一样的。

接下来从公式角度说明这是为什么

注意力机制中的permutation equivariant

假设输入，权重，令：

输出为

取任意置换矩阵（permutation matrix），置换后的输入，有：

这里提一下置换矩阵，置换矩阵的每一行和每一列都恰好有一个1，其余元素都是0的方阵。当一个矩阵乘上一个置换矩阵时，所得到的是原来矩阵的横行（置换矩阵在左）或纵列（置换矩阵在右）经过置换后得到的矩阵。在注意力机制中，每行代表一个token，所以这里选择左乘置换矩阵，行置换。

注意力打分：

因为Softmax是对每一行进行Softmax，不是整个矩阵进行。左乘会行重排，右乘会列重排，但是不影响最后结果，所以：

可以看到，置换输入，输出结果也会进行相应置换。那么这是不是和前面提到的permutation invarient矛盾？

其实不然，我们回顾下permutation invarient，核心是“每一个词向量计算结果不变”。也就是每个token对其他token的加权和不变，只是和相比，现在变为了。

假设之前的如下：

那么置换输入后得到的结果，可能变成了“爱吃我梨子”这个排列顺序的矩阵，但是每个词向量的计算结果不变。

所以，单独看注意力机制，其实是等变（equivariant）的。也就是输入做置换，输出也会被同步置换

但是这样，输出结果还是和原始的不一样，能保证最终的输出结果一样吗？

答案是可以的，要分具体的任务来讲述

permutation invarient导致的输出确定

分类任务

对于分类任务来说，会对注意力权重矩阵进行聚合，也就是执行sum/mean/attention pooling，因为矩阵元素一样，所以最后得到的结果也是一样的。

翻译任务

虽然注意力权重矩阵被置换，但解码器的 cross-attention 会把“换位”抵消掉，生成的翻译（在同样的解码策略和同样的目标前缀下）不变。

需要注意的是，对翻译任务来说。decoder侧的输入，是基于label的。具体来说，假设样本是：“我/爱/机器/学习”和 “i/ love /machine/ learning”。把“我/爱/机器/学习”输入到encoder里去，，而decoder则是”i/ love /machine/ learning”的右移掩码矩阵。所以下面的公式证明中，并不会对解码器的输入乘以置换矩阵。

令解码器第步的查询为，encoder侧给出key/value:

若用置换矩阵打乱源序:

cross-attention 的权重（对每一行做 softmax）：

于是输出的上下文向量

cross-attention后的加权和完全一样，解码器看到的源信息对置换不敏感。自注意力是等变（输出会重排），但cross-attention 的读出是不变（置换对消）。

结论

给定相同词向量（猫，坐在，垫子，上），不论它们在输入里怎么排，模型（不含位置信息）对它们的整体作用是一样的，输出结果是确定的，无法准确建模，需要用位置编码来记录位置信息。

提到permutation invarient这个词，脑海当中应该想到的是“每个词向量的计算结果相同”，仅仅是在矩阵中的位置被置换了，但是最后得到的输出结果是一样的。

那么关键的点为：没有位置编码，交换词顺序，每个词向量的计算结果仍相同。词向量的计算结果相同导致了最后的输出结果相同。

每个词向量的计算结果直接影响最后的输出。

位置编码（Position Encoder）

为什么加上PE，位置信息就不会丢失

因为改变了注意力分数的计算方式。但是严格来说，PE还是会丢失部分位置信息。

模型的输入是由词嵌入和位置编码组合而成。

我们假设位置编码矩阵是，在原始输入和置换后输入两种情况下，添加位置编码：

在标准 Transformer 中，输入向量 是词向量 (Embedding) 和位置向量 (Position) 的直接相加：。

当我们计算 Attention 的 Logits（分数）时，公式是 。
为了简化理解，我们暂时忽略权重矩阵 和

直接看 和 的点积。

$$\begin{aligned} X_i \cdot X_j^T &= (E_i + P_i) \cdot (E_j + P_j)^T \\ &= \underbrace{E_i \cdot E_j^T}_{\text{1. 内容-内容}} + \underbrace{E_i \cdot P_j^T}_{\text{2. 内容-位置}} + \underbrace{P_i \cdot E_j^T}_{\text{3. 位置-内容}} + \underbrace{P_i \cdot P_j^T}_{\text{4. 位置-位置}} \end{aligned}$$

其中就是计算两个词的位置信息，这样注意力分数不再是取决于词向量矩阵。

在进行注意力分数的计算，会发现两者的结果已经不是置换的关系。
最终结果是会包含位置信息，不再仅仅取决于词向量矩阵。

位置编码设计历史

• 用整型值标记位置：给第一个token标记1，给第二个token标记2…，以此类推。导致的问题：模型可能遇见比训练时所用的序列更长的序列。不利于模型的泛化。模型的位置表示是无界的。随着序列长度的增加，位置值会越来越大。
• 用[0,1]范围标记位置：解决了整型值标记位置的问题，但是当序列长度不一样时，token间的相对距离不同。在序列长度为3时，token间的相对距离为0.5；在序列长度为4时，token间的相对距离就变为0.33。相对位置表明句子中每个token之间的距离，不应该随着句子长度变化而变化。

到这里，位置编码的设计理念应该遵从：

• 唯一性：每一个位置（时间步）都必须有一个独一无二的位置编码，不能重复。
• 可扩展性：编码方式应该能自然地推广到比训练时见过的序列更长的序列。
• 确定性：PE必须是确定的（非随机的），不随输入的改变而变化。

二进制编码

考虑到位置信息作用在input embedding上，因此比起用单一的值，更好的方案是用一个和input embedding维度一样的向量来表示位置。这时我们就很容易想到二进制编码。

位置 pos,”二进制表示 (d=3, d=2, d=1, d=0)”
0,0 0 0 0
1,0 0 0 1
2,0 0 1 0
3,0 0 1 1
4,0 1 0 0
5,0 1 0 1
6,0 1 1 0
7,0 1 1 1
8,1 0 0 0

transformer中的d_model足够大（一般为512），很难出现不够用的情况。每个位置的编码也是唯一和确定的。

但是存在一个问题，”这样编码出来的位置向量，处在一个离散的空间中，不同位置间的变化是不连续的。“

具体来说：

pos=6 -> [0, 1, 1, 0]

pos=7 -> [0, 1, 1, 1]

pos=8 -> [1, 0, 0, 0]

模型会看到：PE(6) 和 PE(7) 非常相似（只差1位，距离很近）。但 PE(7) 和 PE(8) 极其不相似（差了4位，距离很远）。模型会认为PE(6) -> PE(7) 是一种变换，而 PE(7) -> PE(8) 是另一种完全不同的变换，无法学习”相邻“这个概念。而在NLP中，“相邻”比“不相邻”理论是具有更高的注意力分数，所以这种“不连续性”对建模是不利的。

所以，我们希望位置编码是具有“连续性”的，

基于三角函数(sin)的位置编码

目前为止，位置编码需要具备：

• 唯一性：每一个位置（时间步）都必须有一个独一无二的位置编码，不能重复。
• 确定性：PE的值应该只取决于位置本身，而不是句子的长度。如果采用[0,1]
• 连续性
• 易于外推

从上面这个二进制编码，如果竖着看，那么可以发现左边的频率小，右边的频率大，是周期性的。具有周期性，且能控制频率大小，函数值有界，可以无限延申。比较容易想到的就是三角函数，每一列赋予一个频率，那么就可以得到位置编码：

”下面差一张图，全部用sin来表示“

不过单独的三角函数虽然具备以上性质，但是却无法满足另一个重要特点：易学习的相对位置。在NLP中，相对位置比绝对位置要更加重要。比如，“猫坐在垫子上，很可爱啊” 和 “很可爱啊，猫坐在垫子上”。词的绝对位置不同，但是语义上没有差别，不会对建模有根本影响。但是相对位置如果变化，可能会导致语义混乱。例如，垫子坐在猫上。而单独的sin函数会受到绝对位置的影响

以下通过公式来证明：

sin位置编码的缺陷

假设我们要计算两个 Token 之间的注意力分数（Attention Score）。Token A 的绝对位置为 。Token B 的绝对位置为 。它们之间的相对距离为 。模型维度为 （假设 是偶数）。位置编码向量 的第 个维度的频率为 （通常 是关于 的递减函数）。我们的目标是观察它们的点积结果：$\text{Score} = PE_m \cdot PE_n = \sum_{j=0}^{d-1} PE(m, j) \cdot PE(n, j)$

假设我们有一个词，它的绝对位置是 。
Transformer 的位置编码 是由一系列不同频率 的sin函数组成的。

我们定义位置 在这个频率下的编码向量 ，于另一个位置 （距离 相对距离为 ），它的编码向量 为

我们要计算的值是：$\text{Score} = \mathbf{p}_t \cdot \mathbf{p}_{t+k}$

假设位置编码是sin函数

$$PE(pos, j) = \sin(\omega_j \cdot pos)$$ $$\begin{aligned} PE_m \cdot PE_n &= \sum_{j=0}^{d-1} \sin(\omega_j m) \cdot \sin(\omega_j n) \end{aligned}$$

根据积化和差公式：

$$\sin A \sin B = \frac{1}{2} [\cos(A - B) - \cos(A + B)]$$

可得：

$$\begin{aligned} PE_m \cdot PE_n &= \sum_{j=0}^{d-1} \frac{1}{2} \left[ \cos(\omega_j(m - n)) - \cos(\omega_j(m + n)) \right] \\ &= \underbrace{\frac{1}{2} \sum_{j=0}^{d-1} \cos(\omega_j \cdot (-k))}_{\text{相对位置项 (OK)}} - \underbrace{\frac{1}{2} \sum_{j=0}^{d-1} \cos(\omega_j \cdot (m + n))}_{\text{绝对位置干扰项 (Fail)}} \end{aligned}$$

上面的公式中存在绝对位置，位置信息会受到绝对位置的影响。如果绝对位置发生变换，那么最终的注意力分数也会受到绝对位置的干扰。

位置编码是Sin 与 Cos 的交替

Transformer中给偶数维度和奇数维度分别使用一个位置编码：

• 偶数维度 ：使用 $\sin$$PE(pos, 2i) = \sin(\omega_i \cdot pos)$
• 奇数维度 ：使用 $\cos$$PE(pos, 2i+1) = \cos(\omega_i \cdot pos)$

计算结果：

$$PE_m \cdot PE_n = \sum_{i=0}^{d/2 - 1} \left( \underbrace{PE(m, 2i) \cdot PE(n, 2i)}_{\text{偶数维乘积}} + \underbrace{PE(m, 2i+1) \cdot PE(n, 2i+1)}_{\text{奇数维乘积}} \right)$$

代入sin 和 cos 定义：

$$PE_m \cdot PE_n = \sum_{i=0}^{d/2 - 1} \left( \sin(\omega_i m) \sin(\omega_i n) + \cos(\omega_i m) \cos(\omega_i n) \right)$$

使用两角差的余弦公式：

$$\cos A \cos B + \sin A \sin B = \cos(A - B)$$ $$PE_m \cdot PE_n = \sum_{i=0}^{d/2 - 1} \cos(\omega_i \cdot (-k)) =\sum_{i=0}^{d/2 - 1} \cos(\omega_i \cdot k)$$

是一个常数，位置信息只和相对位置有关，能够较好的完成建模。

对sin/cos编码的进一步理解

目前已经证明了，选用sin+cos的编码模式能满足：

• 唯一性：每一个位置（时间步）都必须有一个独一无二的位置编码，不能重复。
• 确定性：PE的值应该只取决于位置本身，而不是句子的长度。如果采用[0,1]
• 连续性
• 易于外推
• 易于学习相对位置

在Transformer中，使用的具体位置编码为：

偶数维度：

$$PE(pos, 2i) = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)$$

奇数维度：

$$PE(pos, 2i+1) = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{model}}}}\right)$$

: 单词在序列中的位置
: 词向量维度
: 位置编码向量的索引维度，[, ]

可视化结果：

对pe值进行可视化。d_model=128，横轴是维度，纵轴是pos：

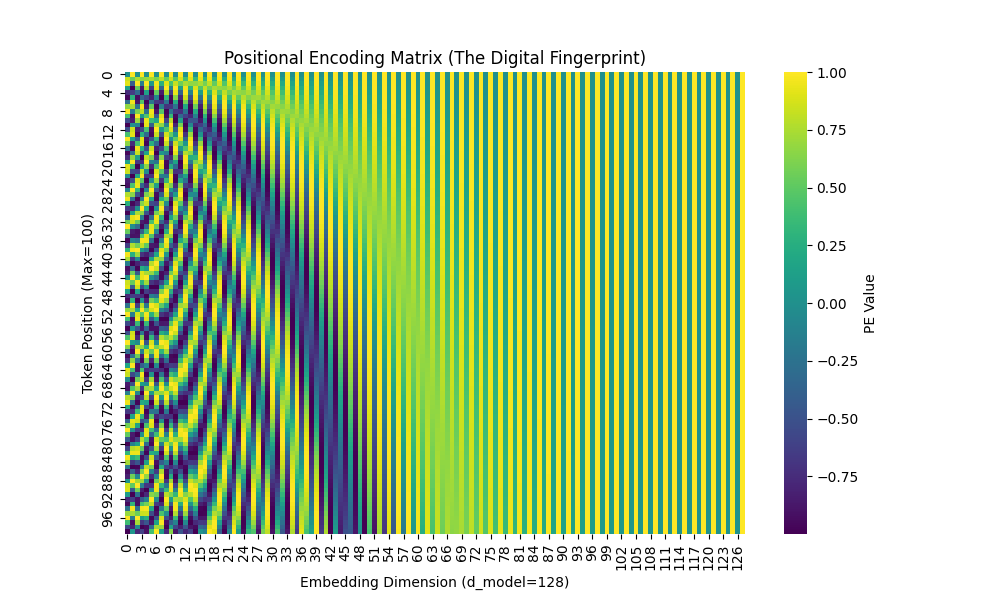
可以看到在低维度区域，PE的变化剧烈，也就是频率高；高维度区域相反。

我们再筛选三个不同频率来看下：

的具体选择（即 ）

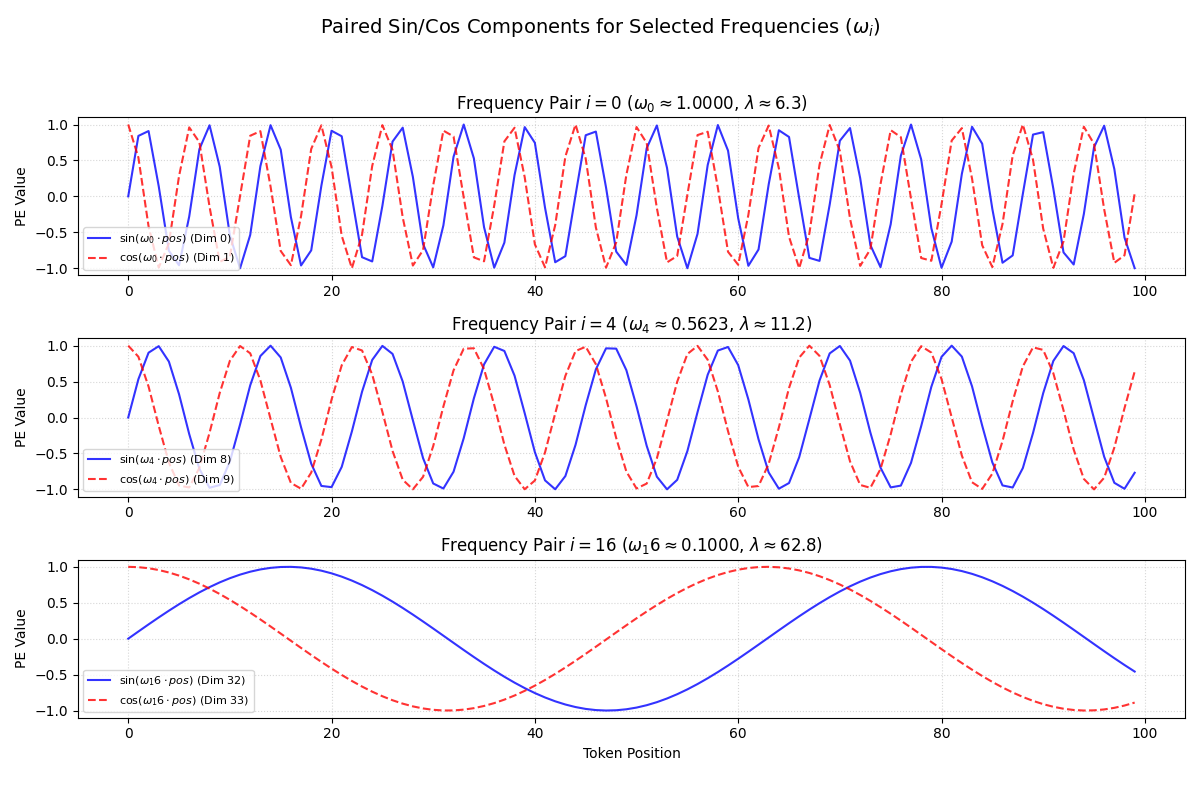
关于几何级数和线性级数的选择，还是有些不理解，后面再说。

Transformer中的位置编码使用了和 的混合编码，的具体选择为。可以进一步分析下为什么这种形式，具体的数值是怎么来的？

几何级数

是一个几何级数，换成线性级数，理论也是可以达到相同的编码要求（例如，唯一性、易学习相对位置等）。

这里我们对比两种 的设计：

• 几何级数（Transformer 采用）： 频率按 衰减，在对数尺度上均匀分布。
• 线性级数（假设）： 频率按固定步长均匀衰减。

修改频率变化情况

trans中位置编码的频率是逐渐衰减的，但是逐渐增加会如何？我还没试过

绝对位置编码

• Sinusoidal (三角函数) 位置编码：Transformer中的位置编码。
• 可学习的 (Learned) 绝对位置编码：创建一个位置编码矩阵，位置编码是模型的参数，通过反向传播从数据中学习得到。优点是简单，模型自己学习最好的位置表示；缺点是无法外推，需要大量数据才能学好。

相对位置编码

这类编码认为：“词A在位置5，词B在位置8” 这个绝对信息，不如 “词B在词A后面3个位置” 这个相对信息重要。

这类方法不再是 X_i = E_i + P_i。

直接修改（hack）注意力机制。当计算 score(i, j) 时，它们会额外注入一个专门表示 i 和 j 之间相对距离（i - j）的向量。

代表模型： Transformer-XL, T5, DeBERTa。

Trans中位置编码存在的局限

不够存粹，存在一些偏置项。

旋转位置编码