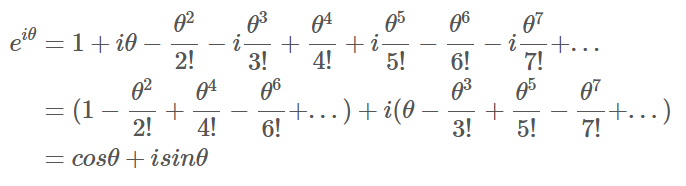复数

参考资料

https://www.cnblogs.com/noluye/p/11964513.html

背景

复数是对实数的扩充，能解决普通实数不能很好解决的问题。

例如：

$$x^2 + 1 = 0$$

实数无法解决这个问题，数学家提出一个很厉害的思想，承认的存在，假设满足，于是前面的方程我们可以解出：

$$x=\pm{i}$$

可以不必纠结是什么，就是数学家提出的数学工具，一个简单的数学对象，满足，关键是复数对于旋转能发挥很重要的作用。

复数定义

复数由两个部分组成：实部（real part）和虚部（imaginary part）。实部就是我们平常遇到的数（正数、负数、0），而虚部是一个实数和的乘积。

不过在 Python 中，复数的符号用表示，在 Jupyter 中运行 Python：

1 z = 3 + 4j
2 z, z.real, z.imag   # 复数、实部、虚部

复数与旋转

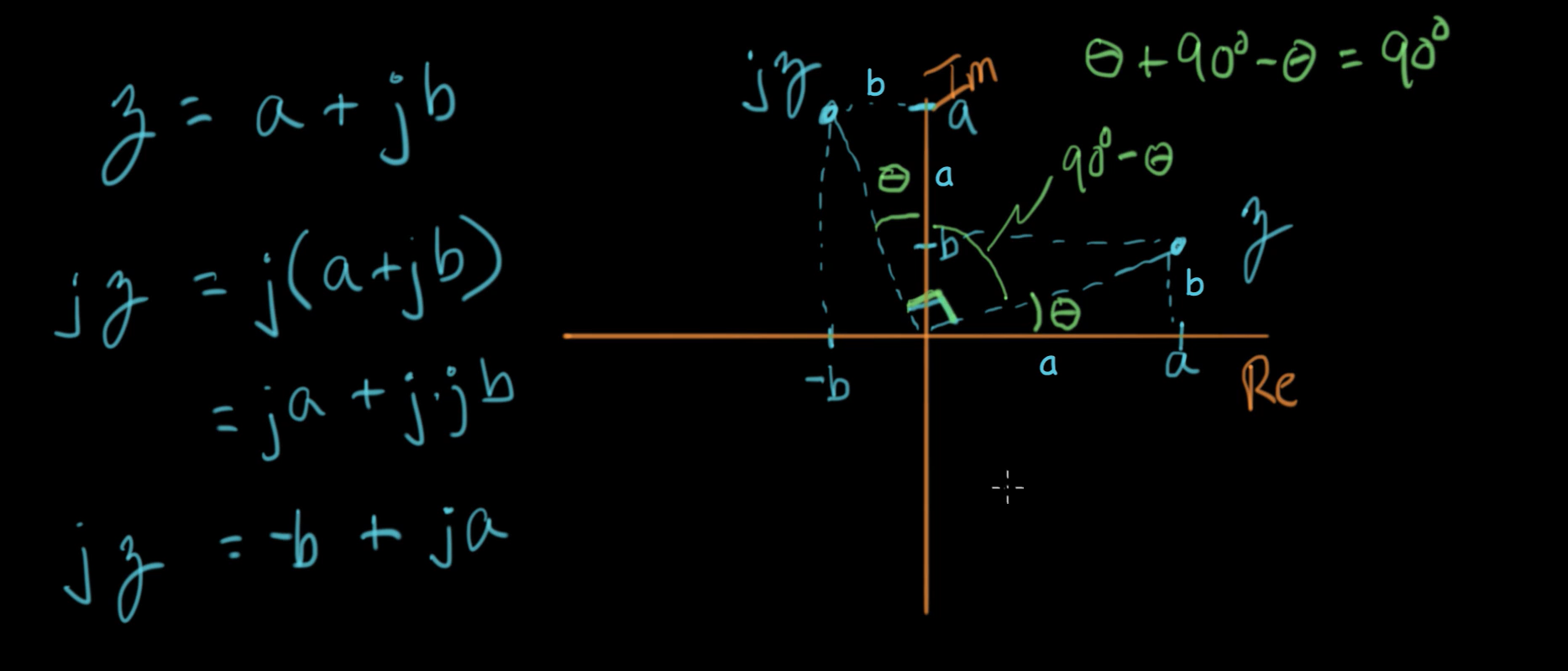
如上图所示，假设一个复数是，乘以后，

这两个向量之间的夹角刚好是90°。
要对一个复数（这个复数在复平面可以表示为一个 2D 向量）旋转 90°，只需乘以即可。如果是旋转180° ，那么就乘以两个，也就是。

极坐标表示

旋转 90°，只需乘以即可。那么自然地，我们就会去进一步思考，如果旋转任意角度应该怎么表达呢？旋转 45° 究竟是乘以 ，还是乘以 ，还是乘以其他的什么东西？

以及，为什么乘以复数会表示旋转？

为了解决这两个问题，我们开始引入复平面上的极坐标表示。

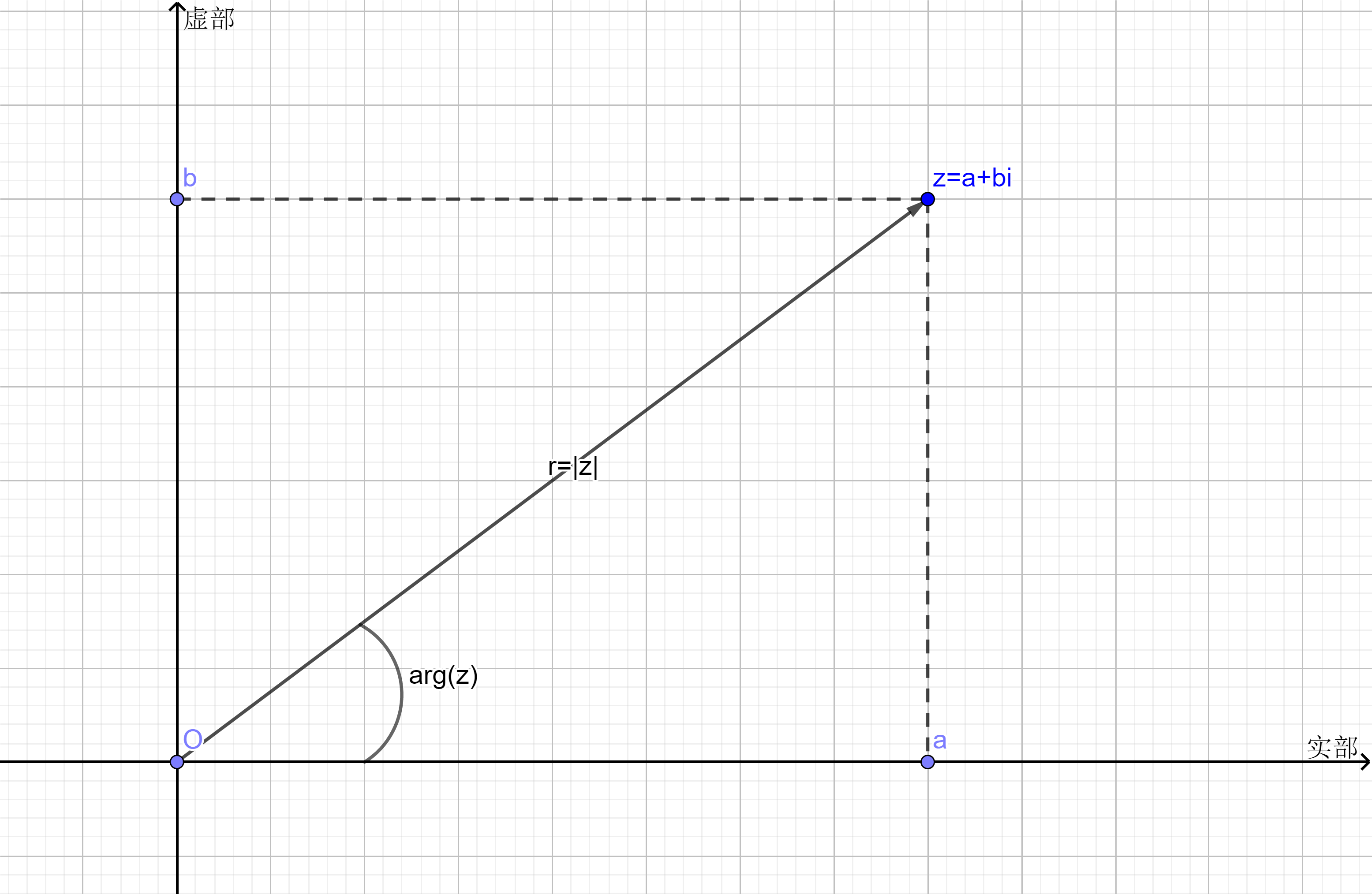
复数可以通过长度 和角度来确定。

长度等于复数的模，而角度是实数轴和复数所表示的向量的夹角，称为幅角（argument）。接下来根据三角函数，我们有
和，可以得到：

$$z=r(cos\theta+isin\theta)$$

根据欧拉公式，复数的极坐标形式可以简写为：

$$z=re^{i\theta}$$

欧拉公式的证明在后面

---

定两个任意用极坐标表示的复数：和，进行乘积，那么我们会得到：

$$z_1z_1=r_1r_2e^{i(\theta_1+\theta_2)}$$

两个复数的乘积得到另一个复数。

它的模等于两个复数的模的乘积：

它的幅角等于两个复数的幅角的和：

于是看起来，考虑复平面这个几何情形，乘以一个复数，可以同时带来两种变换的效果:

1. 长度的缩放（通过改变模长）。

2. 旋转（通过改变幅角）。

旋转子

接下来一个很自然的想法，就是：乘以一个什么样的复数，不会产生缩放，只会产生旋转？

显然，通过前面极坐标下自然底数的表达形式的推导，我们知道乘以一个模为 1 的复数时，不会导致缩放，只会产生旋转。

这样的复数就称为旋转子（rotor），旋转子提供了“纯”旋转动作的数学表示，它可以将复数旋转任意角度。一般而言，将复数旋转角度的旋转子定义为：

$$R_{\theta}=c o s\theta+i s i n\theta=e^{i\theta}$$

如果要对一个复数逆时针 旋转45°，需要乘以：

$$1\cdot e^{i\cdot45^{\circ}}=c o s45^{\circ}+i s i n45^{\circ}={\frac{\sqrt{2}}{2}}+{\frac{\sqrt{2}}{2}}i$$

如果是顺时针旋转呢？那就乘以其共轭复数。

欧拉公式的证明

其中一种证明方法是利用泰勒级数把、和联系起来。

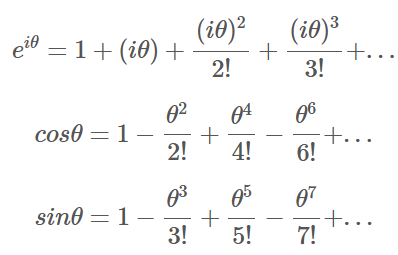
根据，有：