ROPE

基础知识

三角函数

旋转矩阵

https://zhuanlan.zhihu.com/p/183973440

XY坐标系中，向量OP旋转β角度到了OP’的位置：

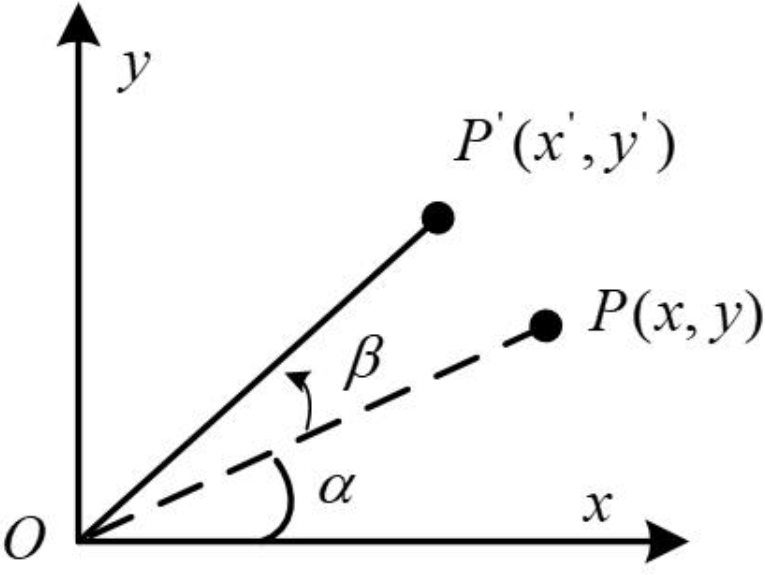
根据三角函数关系，可以列出向量OP与OP’的坐标表示形式：

对比上面个两个式子，将第2个式子展开：

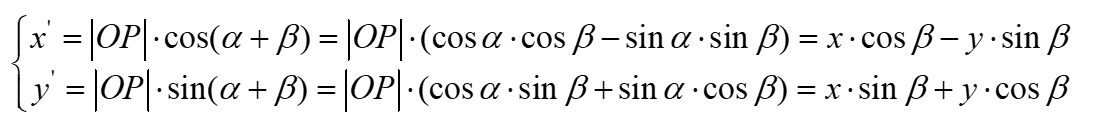
用矩阵形式重新表示为：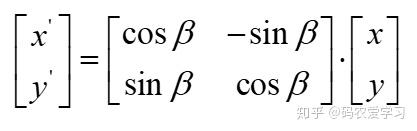

中间的矩阵即二维旋转的旋转矩阵，坐标中的某一向量左乘该矩阵后，即得到这个向量旋转β角后的坐标。

论文核心逻辑

• 背景：Transformer 的自注意力机制（Self-Attention）计算的是 Query 和 Key 的内积。我们需要把位置信息 和 塞进 和 里。
• 目标：我们希望找到一种编码方式 ，使得 Query 和 Key 做内积（Attention Score）之后，结果只包含相对位置 的信息。即： 应该等价于一个函数 。这个函数就是约束，经过位置编码后的 和 的内积，应该等于一个只与“相对距离 ()”有关的函数 ： $$\langle f_q(x_m, m), f_k(x_n, n) \rangle = g(x_m, x_n, m-n)$$
• 推导：
  • 先在 2维空间（复数域）推导，发现 旋转（Rotation） 完美满足上述条件。
  • 再推广到 维空间，通过将向量切分为 个子空间，分别旋转。
• 性质 (Properties, Sec 3.3): 这种旋转编码自带“远程衰减”特性，符合语言规律。

一些问题

问题1

论文公式（4）中的。看起来有些不对，因为一般是右乘词嵌入矩阵。右乘的时候，我们默认词嵌入矩阵是一个行向量；而论文这里使用左乘，应该是将向量 视为列向量。

问题2

公式2下面的公式，咋一看有些不对，但是仔细看，可以这样去理解。

是第 个位置的注意力分数输出，固定，然后遍历整个序列，所以这个公式是没有问题的。

公式解读

公式1

表示的是第个token，而表示这个token的位置索引。

只是一个向量，没有位置。

ROPE需要拿着 （向量），根据 （位置整数）计算出一个旋转角度 ，然后把向量转一下。如果不传 ，函数就不知道该转多少度。

公式18a

论文写的是

应该是写错了，按照上面的公式，推导下来应该是：

按照论文的推导，可以得到：

$$R_g(x_q, x_k, 0) = R_q(x_q, 0) \cdot R_k(x_k, 0) =||q|| \cdot ||k|| =$$

比较难理解的在于

可以这样理解：

公式14，论文原文解释说，可以理解为“带有空位置信息的向量” (vectors with empty position information encoded) 。也就是说， 就是还没有旋转过的初始 Query 向量。

再看公式17，是在初始条件下（m=0）的情况下得到的。

$$\underbrace{q}_{\text{向量符号}} = \underbrace{||q|| e^{i\theta_q}}_{\text{向量的极坐标表示}} = \underbrace{R_q(x_q, 0) e^{i\Theta_q(x_q, 0)}}_{\text{函数的极坐标定义}}$$

前一个都好推导，因为这里是假设二维平面，是一个二维向量，用极坐标写出来就好。

• 中间项 ：这是复数 的标准写法。
  • 表示向量 的模长（也就是长度）。
  • 表示向量 的原本角度。

后一部分，需要和公式15结合，把m=0代入就好。

• 右边项 ：这是位置编码函数 在 时的写法。
  • 是函数定义的模长部分。
  • 是函数定义的角度部分。

要想让公式成立，那么模长和模长要相等，辐角和辐角也相等。所以：

$$R_q(x_q, 0) = ||q||$$ $$R_k(x_k, 0) = ||k||$$

在这个基础上，回到公式18a就能得到：

$$R_g(x_q, x_k, 0) = R_q(x_q, 0) \cdot R_k(x_k, 0) =||q|| \cdot ||k|| =$$

那么也就推出了，在m=n的条件下：

$$R_q(x_q, m)=R_k(x_k, 0)=||q|| \cdot ||k||$$

公式16第二行

这个公式是公式15和公式16的结合，理论上应该是下面这个才对：

$$\Theta_k(x_k, n) + \Theta_q(x_q, m) = \Theta_g(x_q, x_k, n-m)$$

而公式16第二行给出的是：

$$\Theta_k(x_k, n) - \Theta_q(x_q, m) = \Theta_g(x_q, x_k, n-m)$$

关键在于为什么是减号而不是加号？

原因在于取了转置，在复平面上，就是共轭转置

维度和向量

向量的解释有很多种，空间中的箭头、有序的列表等都是正确的：

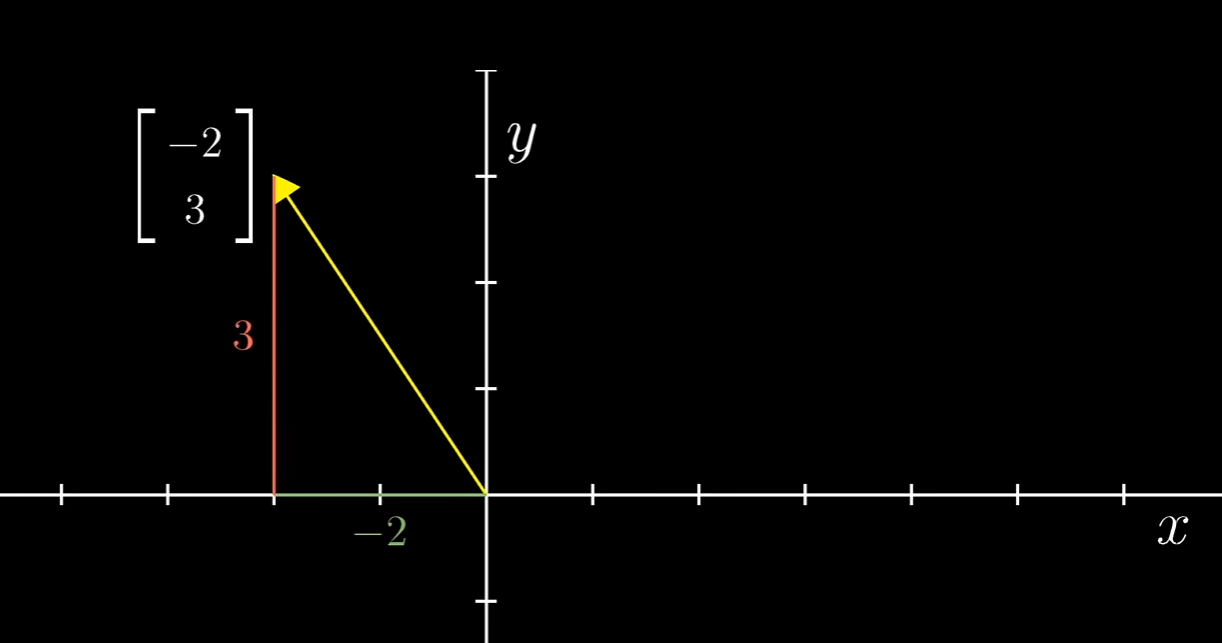
如果在平面当中，这就是一个二维向量。对于每个token来说，它是一个维向量。这里一定要和矩阵区分开来。

在ROPE的论文里面，为了方便推导，先从d=2，也就是二维向量开始推导。然后推广到多维。

前提知识

公式4：这个公式以二维复平面为例进行示例并推导公式。我们先说二维平面，在二维空间中，设两个实数向量为 和 ，它们的点积是：

$$\mathbf{q} \cdot \mathbf{k} = x_1 x_2 + y_1 y_2$$

现在来到复平面，把这两个向量看作复数 和 。
这时候，如果我们计算复数内积（ 乘以 的共轭 ）：

$$\begin{aligned} q \cdot k^* &= (x_1 + i y_1)(x_2 - i y_2) \\ &= (x_1 x_2 + y_1 y_2) + i (y_1 x_2 - x_1 y_2) \end{aligned}$$

实部就是我们需要的点积结果

而公式4之所以写成了极坐标形式而不是复数形式，是为了后面更好的推导。因为论文是通过“旋转”来施加位置编码，说的更细一点，就是转动一定的角度来赋予位置编码。而极坐标是由模长和角度两部分组成，使用极坐标，能直观的看到角度的变化。

3.4小节解读

首先3.4小节明确了是二维的情况。按照公式1的说法：

表示的是第个token，而表示这个token的位置索引。

只是一个向量，没有位置。

那么是一个二维向量，而且论文把q进行转置，说明是按照列排序，而不是传统的行排序。行排序是w进行转置。

所以在3.4小节中，是一个竖排向量，转置后就是横排，和做内积，得到的是一个标量。

因为作者借助复数来推导，所以后面的内积是复数域的内积。

对于二维向量来说，内积就是对应部分乘积然后相加。

内积的符号：<>

a=[3,2]
b=[4,6]
= 12+12=24

推广到复数域：a=3+2i; b=4+6i

如果直接计算内积：=12+26i-12
因为内积是标量，所以会对计算结果取实部，但是结果显然不对，应该乘以后面那个复数的共轭。

= Re[ab*]

---

公式12：是一个二维向量，列排列，表示的是某个token，就是query，是key。和就是论文的目标：找到一种编码方式 ，使得 Query 和 Key 做内积（Attention Score）之后，结果只包含相对位置 的信息。所以看到和，可以进一步理解为，根据输入和其位置索引m，对这个输入进行旋转，赋予其位置信息。因为论文中是通过旋转赋予位置编码，那么和的区别就是幅角。

公式13：没啥好说的，query和key做内积

公式14：论文原文解释说，可以理解为“带有空位置信息的向量” (vectors with empty position information encoded) 。也就是说， 就是还没有旋转过的向量。

公式15：把公式12和公式13从二维平面推广到复数平面，使用极坐标的方式表示，前面的是模长，后面的幅角。

公式16：因为公式13，f_q和f_k做内积，会得到g的函数。现在要把极坐标的形式进行代入。因为极坐标的乘法是模长和模长相乘，幅角和幅角相乘。所以公式16的第一个式子没有问题。第二个式子因为是极坐标形式，做内积的时候，后面那一项需要取共轭，所以前面应该有个负号，但是实际论文中好像是反过来了。我也不知道为什么，但似乎不影响。正确的应该是：

$$\Theta_{q}(x_{q},m)-\Theta_{k}(x_{k},n)$$

公式17：和公式14差不多，是一个初始条件。假定位置是0，也就是旋转角度为0。

公式17应该和公式14放在一起，或者说公式17是公式14的进一步展开。q,k在二维平面上用极坐标表示，原始的角度是和。后面就是公式15的写法。从公式17的等式中，能得到两个推论：

k也是同样的，这个推论在公式18会用到。这个推论，其实和公式19一样。不过不重要，只要能推导出来就行。

公式18：论文写的不清楚，而且可能有些笔误，按照我的方式来理解：

论文是要证明这个结论：

$$R_{q}(x_{q},m)R_{k}(x_{k},m)=\|q\||k\|$$

根据公式16可以得到：

再根据公式16，如果m和n都取0，也可以得到

所以：

$$R_{q}(x_{q},m)R_{k}(x_{k},m)=R_{g}(x_{q},x_{k},0)=R_{q}(x_{q},0)R_{k}(x_{k},0)$$

再根据公式17的推论。

就可以得到：

$$R_{q}(x_{q},m)R_{k}(x_{k},m)=\|q\||k\|$$

公式19：跳过，推论可以由公式17得到

过度公式：$\Theta_k(x_k, m) - \Theta_q(x_q, m) = \theta_k - \theta_q$

这个是由公式18b移动项得到的，这样看这个公式会好理解些：

$$\underbrace{\Theta_q(x_q, m) - \theta_q}_{\text{Query 的角度增量}} = \underbrace{\Theta_k(x_k, m) - \theta_k}_{\text{Key 的角度增量}}$$

这个公式得出一个结论，那就是Query 的角度增量和Key 的角度增量相同。这里关键是要理解这个差值相同，可以想象一个图辅助理解，假设q的初始角度是10，k的初始角度是20。那么q转动到35，k转动到45，两边的增量都是25。核心的点在于转了多少，而不是最后的角度是多少，而转了多少，是和m有关。

既然“角度的增量”只与 有关，作者就定义了一个只与 有关的函数 来表示这个增量：

$$\Theta(x, m) - \theta = \phi(m)$$

把 移到等式右边，就得到了 公式 20 3：

$$\Theta_f(x_{\{q,k\}}, m) = \phi(m) + \theta_{\{q,k\}}$$

公式21：代入到公式16里面推一下就好，不难。

公式22：公式21的右边是一个常数，可以写为一个常数。

$$\phi(m+1) - \phi(m) = \theta$$

我们要解出 是什么：

• 当 时：
• 当 时：
• 当 时：
• 推广到m:

$$\phi(m) = \phi(0) + m \cdot \theta$$

对应到公式22：

$$\phi(m) = m\theta + \gamma$$

和都是常数，非0。

公式23到公式25的推导没有什么太难的，就是公式25中的把要稍微解释下。

根据之前的推导，位置编码的相位函数（角度）是：

$$\text{总角度}(m) = \underbrace{\theta_q}_{\text{原始角度}} + \underbrace{m\theta}_{\text{位置旋转}} + \underbrace{\gamma}_{\text{初始偏移}}$$

如果m=0，也就是第一个token，会在原有角度上旋转一个角度。

但是相邻 token 的角度差异还是 ，并不影响模型捕捉相对位置依赖关系的能力（因为在计算 Attention 内积时， 会在相减过程中被抵消掉），所以可以令 ，看起来更加简洁。核心就是为了方便和简洁。

我们以论文中q和k的内积为例，在公式16中。

如果保留 ，Query 和 Key 的角度分别是：

这两个部分对于公式16中的m和n，相减会直接把 抵消。

3.2.1小节解读

公式4没什么好说的。需要注意的就是复数做内积，后面那个复数需要取共轭。

公式5：是数学公式中的一种“省流写法”，表示适用于 ，也适用于 ，这里的下标 是一个集合记号，意思是你可以从 中任选一个代入。

明白了这个，我们来解释下公式5。首先我们要明白，公式5表达的是对输入赋予位置编码，论文的位置编码是通过旋转得到的，所以公式里面会出现旋转矩阵。

$$f_{\{q,k\}}(x_m, m) = \underbrace{\begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix}}_{\text{第一部分 (矩阵 A)}} \cdot \underbrace{\begin{pmatrix} W^{(11)} & W^{(12)} \\ W^{(21)} & W^{(22)} \end{pmatrix}}_{\text{第二部分 (矩阵 B)}} \cdot \underbrace{\begin{pmatrix} x^{(1)} \\ x^{(2)} \end{pmatrix}}_{\text{第三部分 (向量 C)}}$$

因为输入的是这个token，位置是m，而且是二维向量。所以在最右边是两个分量，列排列。

中间是参数矩阵，一般来说维度是 $dd22 $，也没有问题。

最左边是旋转矩阵。根据3.4小节的推导，从最后的公式25可以看出，加位置编码就是乘以

设（对应向量 ）。
乘以 ：

$$(u + iv)(\cos(m\theta) + i\sin(m\theta))$$

展开：
新实部 (Real)：

新虚部 (Imag)：

写回矩阵形式 把上面的计算过程写成矩阵形式：

$$\begin{pmatrix} \text{New Real} \\ \text{New Imag} \end{pmatrix} = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix}$$

3.4.3小节

这一节主要是说明证明论文提出的位置编码满足两个特性：有上界、长距离衰减（两个位置越远的token，注意力分数越低。但不是单调下降，而是震荡下降）

有界我们很容易想到，就是函数值<=某个值就好。所以公式29使用缩放很好理解，并且缩放的公式也很简单。。但是论文并不是直接就得到公式29，而是由公式28做了铺垫。

是相邻频率分量上的词向量内容的差值。我们不管它具体是多少，直接取其中最大的那个值，记作 。那么可以得到

因为要说明长距离衰减，那就是m-n越大，值越小，而公式29中和m-n相关的项只为

把无关变量给移出去，也就是。

以上就是3.4.3小节的要表达的核心思想以及相关公式解读。接下来，从头来一遍。

---

公式27：没什么好说的，根据前面的公式推论，公式8和公式25结合下就得到了，然后取实部，就是注意力相似度。这个地方做了一个分组，就是两两配对。

公式28：这一步是为公式29做铺垫，为了把m-n这个变量单独剥离出来分析。理论上来说，如果直接把公式28的极坐标写为复数形式再去实部，那么实部内容如下：

$$\text{Attention Score} \propto \sum_{i=0}^{d/2-1} (\text{内容}_i) \times \cos((m-n)\theta_i)$$

咋一看实部多了一个 ，范围就是 [-1,1]。所以这个函数的取值其实取决于 。因为公式29只是把换成了h。那么每一项的值不就是在 之间，当然是有界的。那么是否没有必要进行什么阿贝尔变化？

其实不然，因为这个操作是求和操作，而不是单项操作。

如果有 个项（比如 384 个）。如果这些 全都等于 1（相位对齐），那么总和会非常大（等于 ）。

作者想证明的：随着距离 变大，这些 项不会同时等于 1，而是会有正有负，互相抵消。因此，总和（Attention Score）的上限会大幅下降，远小于 。

阿贝尔变化的作用在于把“互相抵消”这件事（隐藏在 里）和“内容幅度”这件事（）分离开来，让我们能单独证明：位置结构本身会导致总和变小。

把“内容幅度”这件事（）单独拿出来后，后面使用缩放：

$$\dots \le (\max_{j}|h_{j+1}-h_{j}|) \sum |S_{i+1}|$$

是做了最坏的一个假设，假设你的词向量内容 是任意的（只要不是故意针对 RoPE 构造的恶性数据），那么 Attention 分数的衰减趋势主要由 决定。但是如果 本身随着 剧烈变化且刚好抵消了 的衰减，那确实会失效。但在自然语言训练出的模型中，词向量在不同频率分量上的分布通常比较平滑，所以这个假设在统计上是成立的。

至于图2中出现的衰减，因为本质是复数旋转（波的干涉），只要是波，就会有波峰波谷。在某些特定的距离下（波长整数倍），Attention 分数可能会突然回升一点点，这是正常的数学现象。其实核心是 的取值，正是因为这个特定的底数 10000 和指数分布，导致了不同维度的旋转速度差异巨大，从而在长距离下产生了强烈的“相消干涉”。如果 选得不好（比如全是常数），根本不会衰减。

我们需要明白的是：

Decay 的来源：RoPE 的长距离衰减不是像 ALiBi 那样加一个硬性的 Bias 惩罚，而是通过多频率正弦波的干涉自然形成的。

的重要性：那个 base=10000 很关键。后来 LLaMA 做 Long Context 扩展（NTK-Aware, Linear Scaling）时，改的就是这个 的分布。如果你理解了衰减来自于频率差异，你就懂了为什么改 可以扩展上下文长度。

工程与理论的差距：理论证明它是“震荡衰减”的，这就解释了为什么有时候 RoPE 在超长距离下还是会有一些奇怪的“回光返照”（Attention 突然变大），因为那是波的特性。

震荡衰减、知道 有影响、知道 是关键

实验

一、 总体框架 (The Big Picture)

核心目标：证明 RoPE 不仅仅是数学推导漂亮，而且在实际工程中具有 收敛速度快、效果更好、兼容线性 Attention 以及 处理长文本能力强 等优势。

4 个验证维度：

1. 标准任务验证：机器翻译（Transformer 的“老本行”）。
2. 预训练模型验证 (BERT)：考察在预训练（Pre-training）和下游任务微调（Fine-tuning）中的表现。
3. 线性 Attention 兼容性验证 (Performer)：证明 RoPE 可以无缝接入线性复杂度模型（这是很多相对位置编码做不到的）。
4. 长文本与大规模模型验证：中文长文本任务 + GPT-3 架构上的扩展性对比（与 EleutherAI 合作）。

二、 详细实验解读

1. 机器翻译 (Machine Translation)
   这是 Transformer 架构最经典的测试床。

• 设定：使用 WMT 2014 英德翻译数据集 1。对比模型包括标准的 Transformer (Baseline) 和使用相对位置编码 (RPE) 的模型。
• 结果：RoFormer 的 BLEU 分数为 27.5，不仅超过了基线 Transformer (26.5)，也超过了其他的 RPE 模型 (26.8)
• 结论：RoPE 在最基础的序列到序列任务上是有效的，且优于现有的位置编码方案。

1. BERT 预训练与微调 (Pre-training Language Modeling)
   这一部分验证 RoPE 在“理解型”预训练模型中的表现。

• 预训练 (Pre-training)：
  • 设定：用 RoPE 替换 BERT 中的绝对位置编码，在 BookCorpus 和 Wikipedia 上进行预训练 4444。
  • 结果：从 Loss 曲线（Fig 3 左图）可以看出，RoFormer 的 收敛速度比 BERT 更快。
• 微调 (Fine-tuning)：
  • 设定：在 GLUE 基准数据集（MRPC, SST-2, QNLI 等）上进行评估。
  • 结果：在 6 个数据集的对比中，RoFormer 在 3 个数据集上显著优于 BERT，特别是在 MRPC (+1.1%) 和 STS-B (+1.9%) 上提升明显 7777。

1. 线性 Attention 的兼容性 (Performer with RoPE)
   这是一个非常有技术含量的实验。因为大多数相对位置编码（如 T5 的 RPE）是加在 Attention 矩阵上的，这会破坏 Linear Attention 的分解结构，导致无法使用。而 RoPE 是乘在 上的，理论上可以兼容。

• 设定：使用 Performer 模型（一种线性复杂度的 Transformer），在 Enwik8 数据集上训练。
• 结果：加入 RoPE 后，Performer 的训练 Loss 下降得更快，收敛更好（Fig 3 右图）。
• 结论：RoPE 是目前为数不多能直接用于 Linear Attention 的相对位置编码方案，这证明了其数学形式的优越性 10。

1. 长文本与大规模模型 (Long Text & GPT-3)
   这一部分验证 RoPE 的两个重要特性：长距离建模能力 和 在大参数模型上的稳定性。

• 中文长文本 (Chinese Data)：
  • 任务：CAIL2019-SCM（法律文书相似度匹配），文档长度通常超过 512。
  • 结果：RoFormer 随着序列长度增加（从 512 到 1536），准确率稳步提升 12121212。这验证了 RoPE 在处理长文本时的泛化能力。
• GPT-3 架构对比 (with EleutherAI)：
  • 设定：对比了三种编码方式：GPT-3 原版绝对位置编码 (Learned)、T5 的相对位置编码 (RPE) 和 RoPE 13。测试了小模型 (125M) 和大模型 (1.4B) 。
  • 结果：
    • 收敛极快：RoPE 在小模型上仅用 <55% 的步数就达到了其他模型原本的性能 15。
    • 效果更优：在 Validation Loss 和 PPL（困惑度）指标上，RoPE 均击败了原版 GPT-3 和 T5-RPE 16。三、

验证了数学直觉：你在数学推导中看到的“长距离衰减”性质，在中文长文本实验中得到了验证（模型没有因为距离变长而崩盘，反而利用得很好）。

验证了计算优势：Performer 的实验证明了 RoPE 确实是通过“旋转向量”而非“操作 Attention 矩阵”来实现位置编码的，这种解耦让它能适应各种变体架构。

验证了训练效率：多个实验都提到了 “Faster Convergence”（更快的收敛），这意味着用 RoPE 训练模型更省钱、更高效。