SimVP: Towards Simple yet Powerful Spatiotemporal Predictive Learning
模型架构
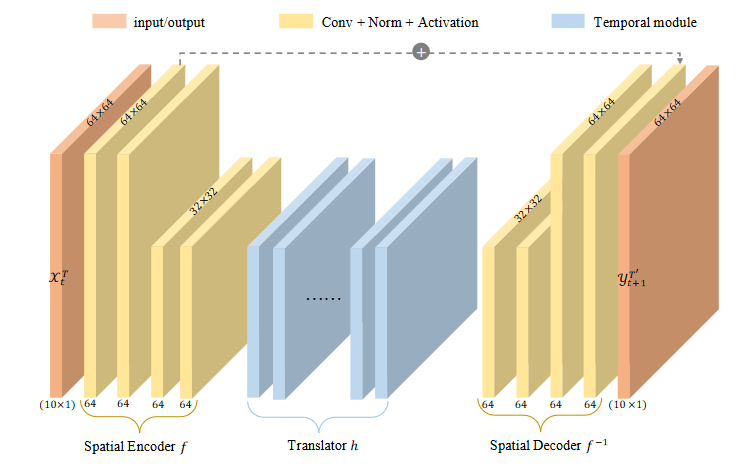
三部分均由CNN组成
其中Translator有两种选择:
IncepU: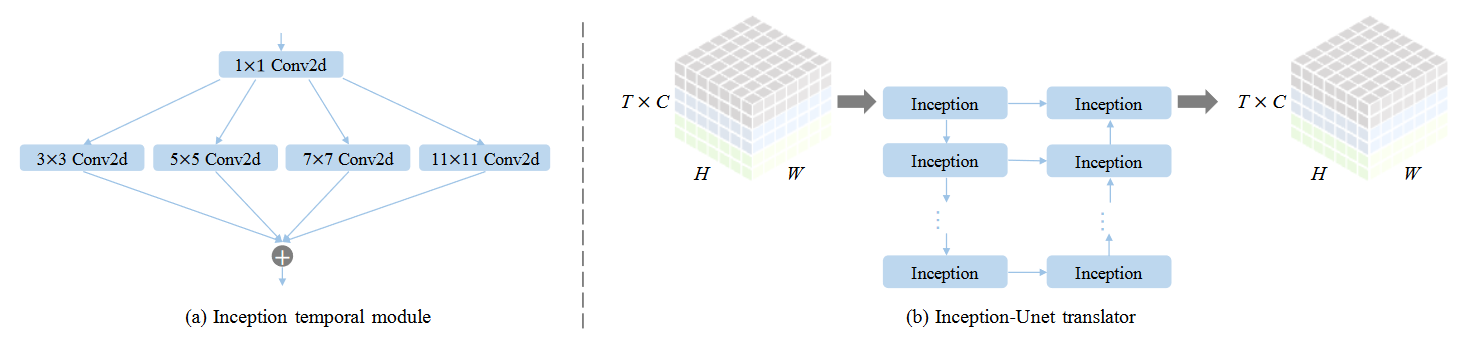
gSTA: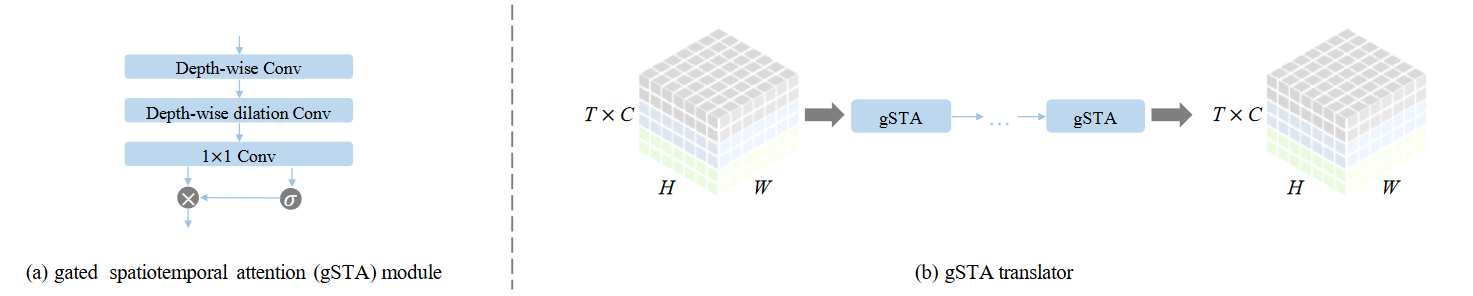
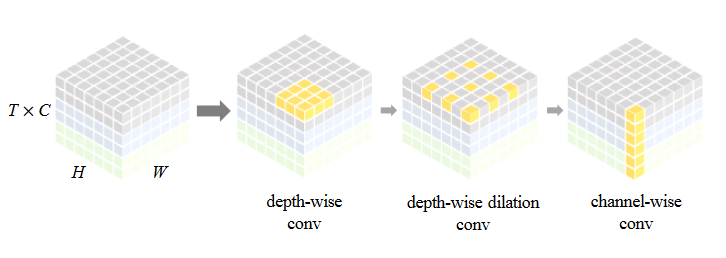
Temporal Attention Unit: Towards Efficient Spatiotemporal Predictive Learning
Summary
(写完笔记之后最后填,概述文章的内容,以后查阅笔记的时候先看这一段。注:写文章summary切记需要通过自己的思考,用自己的语言描述。忌讳直接Ctrl + c原文。)
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
- 准确的时空预测学习可以使气候变化[74, 77]、人类运动预测[91, 107]、交通流量预测[18, 97]和表征学习[39, 71]等领域的广泛实际应用受益。时空预测学习的意义主要在于其探索物理世界中空间相关性和时间演化的潜力。
- 此外,时空预测学习的自监督性质非常符合人类的学习方式,无需大量标记数据。海量视频可提供丰富的视觉信息,使时空预测学习成为一种生成性预训练策略[35, 60],用于特征表征学习,以完成各种下游视觉监督任务。
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?)
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
TIMER-XL: LONG-CONTEXT TRANSFORMERS FOR UNIFIED TIME SERIES FORECASTING
Summary
(写完笔记之后最后填,概述文章的内容,以后查阅笔记的时候先看这一段。注:写文章summary切记需要通过自己的思考,用自己的语言描述。忌讳直接Ctrl + c原文。)
- 这个工作是在“Timer: Generative Pre-trained Transformers Are Large Time Series Models”的工作基础上进行优化的,是同一批人做的。
- 实验是在A100上面进行的。
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
Transformer被广泛应用于时间序列预测,
不论是
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?)
- 现有的时序Transformer通常只能运行(输入/输出)百个量级的时序tokens,而自然语言和视觉的Transformer可以学习数千到数百万个tokens之间的依赖关系。
为什么现有的时序Transformer通常只能运行(输入/输出)百个量级的时序tokens?
这篇论文在说明这一点的时候引用了一篇论文(A time series is worth 64 words: Long-term forecasting with transformers. arXiv preprint arXiv:2211.14730, 2022.)
在引文中的附录A.1.2中提到:“The default look-back windows for different baseline models could be different. For Transformerbased models, the default look-back window is L = 96; and for DLinear, the default look-back window is L = 336. The reason of this difference is that Transformer-based baselines are easy to overfit when look-back window is long while DLinear tend to underfit. ”
大概的意思就是窗口过大,基于Transformer的模型容易过拟合,而基于Dlinear的模型容易欠拟合。但是这篇引文没有分析为什么容易过拟合
- 对于单变量预测,短语境输入导致对全局趋势的学习不足,难以解决现实世界时间序列中的非平稳性问题(Hyndman,2018)。对于多变量预测,越来越多的研究证明了明确捕捉通道内和通道间依赖关系的有效性(Zhang & Yan,2022;Liu et al.,2023;2024a),这凸显了扩展上下文长度以涵盖相互关联的时间序列的实际紧迫性。
- 这里解释下对于多变量预测来说,为什么捕捉通道内和通道间依赖关系和上下文长度有关。
- 对于通道内依赖:指同一变量在不同时间点的依赖关系(例如,温度序列中的季节性变化)。如果上下文长度过短,模型可能无法捕捉到长期趋势(如年周期、周周期),导致预测失败。例如,预测电力负荷时,若上下文仅包含几天数据,模型可能无法学习到夏季高温的长期规律。
- 对于通道间依赖:指不同变量之间的相互作用(例如,温度与电力负荷的关系)。如果变量间的依赖关系是跨时间的(如某地降雨量在几周后影响另一地的农业产量),模型必须看到足够长的历史数据才能学习这种延迟关联。例如,在气候预测中,风速和气压的长期关联可能需要数月的数据来建模。
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
- 提出了多变量下一个标记预测和统一的时间序列预测,通过扩大上下文来强化 Transformers,从而做出信息完整的预测。
- 介绍了 TimeAttention,这是一种为多维时间序列量身定制的新型因果自关注,可通过位置感知促进序列内和序列间建模,并保持 Transformers 的因果性和可扩展性。
- TimeAttention: 旨在捕获所有变量内部和变量之间的因果patches依赖关系
将一维序列扩展到二维时序
论文提出的机制关键在于:(1)彻底捕捉序列内和序列间的依赖关系;(2)在时间维度内保持因果关系。在不失一般性的前提下,我们以多元预测为例进行说明。
多元next token prediction这种范式的好处是可以学习每个序列中的因果依赖关系,同时纳入来自其他序列的外生变量相关性,从而使其成为一种通用预测范式,其性能优于与渠道无关的模型(Nie 等人,2022 年)或以变量为中心的模型(Liu 等人,2023 年)。
上面这段话我不是很理解,没有解释为什么,公式也实在看不出他说的“学习因果依赖关系”和“纳入来自其他序列的外生变量相关性”。等看到后面的论文看能不能解决这个问题。
Position Embedding:使用了RoPE(Su 等人,2024 年),这是一种在时间维度上广泛使用的位置嵌入。在变量维度上,我们在每个头部使用两个可学习标量,以保持变量的排列等价性(Woo 等人,2024 年)。
TimeAttention:与按变量分类(Liu 等人,2023 年)和按非因果关系分类的补丁标记(Nie 等人,2022 年 就是patchTST)不同,我们的 TimeAttention(时间注意)旨在捕捉所有变量内部和变量之间的因果patch-wise依赖关系。
具体来说以时间优先的方式将补丁标记的二维索引平铺为一维索引,从而对补丁标记进行排序。请注意,变量的顺序并不重要,因为等式 6 保证了它们的排列等价性。
作者的方法是在transformer基础上进行优化,核心优化点有两个:Position Embedding和TimeAttention
论文提出的注意力机制,主要是:(1)捕获序列内部和序列之间的依赖关系(对应下面的Position Embedding);(2)在时间维度内保持因果关系(对应TimeAttention)。
Position Embedding
为了避免自注意力中的置换不变性:
- 时间维度:反映token在时间维度上的顺序。
- 变量维度:对变量具有置换不变性。即打乱变量的输入顺序不应改变模型学到的内在规律。
为此,Timer-XL采用了组合式位置编码:
- 对于时间维度: 采用了 RoPE(Rotary Position Embedding。Roformer: Enhanced transformer with rotary position embedding)。RoPE不是简单地将位置编号加在令牌嵌入上,而是通过旋转矩阵的方式将相对位置信息注入到查询(Q)和键(K)向量中。
- 对于变量维度: 在每个头(这个头有可能是指多头注意力机制的头)中引入了可学习的标量 u和 v,以保持变量的置换不变性(这个也是引用了别人的方法,Unified training of universal time series forecasting transformers)。
其实就是简单的把两个方法拼接起来,说的是在E.3提供了详细的消融实验来证明有效性,但是内容很少,全是文字,没有实验。
TimeAttention
旨在捕获变量内部和变量之间的causal patch-wise 依赖。以时间优先的方式将二维索引展平为一维索引,因为有前面的Position Embedding,所以变量顺序不重要。
其原理可以通过以下步骤理解:
- 令牌排序与问题定义
首先,模型将2D的 N(变量数) × T(时间patch数) 的令牌,按照 “时间优先” 的顺序拍平成一条长度为 N*T的1D序列。也就是说,排序是:[Var1-T1, Var1-T2, …, Var1-TT, Var2-T1, …, VarN-TT]。
所谓的时间优先,排列得到的序列应该是按照时间顺序来排列的,应该是:[Var1-T1, Var2-T1,…,Var1-T2, Var2-T2,…, Var1-Tn, Var2-Tn,…]
论文中的这段话:
We provide an intuitive example to illustrate the causal dependencies within multivariate time series: considering the 2nd token of time series A. To predict its next token, its representation h should be exactly dependent on the tokens-{1, 2, 4, 5}.
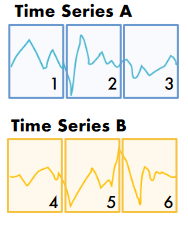
上图按照时间优先,排列成一维顺序应该为:[1,4,2,5,3,6]
所以才说,如果预测序列A的第二个token的下一个token(第三个),只能依赖1,4,2,5。这样看就是正确的。
现在需要一个 (NT) × (NT)的注意力掩码矩阵,这个矩阵定义了在这 NT个令牌中,哪些令牌对之间有依赖关系。
- 依赖关系的解构与克罗内克积(Kronecker Product)
论文发现,这个庞大的、看似复杂的注意力掩码矩阵 A,可以优雅地解构为两个更小矩阵的克罗内克积:
A = C ⊗ T
C(变量依赖图): 一个 N × N的矩阵,表示变量之间的依赖关系。C_{m,n} = 1表示变量 m和变量 n之间存在依赖关系。
T(时序因果掩码): 一个 T × T的下三角矩阵(可能包含对角线),用于保证时间上的因果性。T矩阵中的元素 T_{i,j} = 1(j <= i)。
- TimeAttention的运作机制
克罗内克积 ⊗的效果是,用 C矩阵中的每一个元素 C_{m,n}去“放大”整个 T矩阵。
如果 C_{m,n} = 1,那么在最终的注意力掩码 A中,变量 m的所有时间令牌与变量 n的所有时间令牌之间的依赖关系,就完全由 T矩阵定义(即保持因果性)。
如果 C_{m,n} = 0,那么变量 m和 n之间的所有令牌对都会被掩码掉(即不允许互相注意)。
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
从三个方面对Timer-XL进行评价:
- 作为特定任务的预测器(Supervised training as a task-specific forecaster):
- 这个方面关注的是模型在有监督训练下,在各个独立、具体的预测任务上的性能。这正是通过第4.1、4.2、4.3节分别在单变量预测、多变量预测、协变量预测这三个经典且不同的任务场景上做实验来体现的。每一节都是在某个特定任务上“从头训练”一个模型,并证明Timer-XL在该任务上的优越性。
- 作为零样本预测器(Large-scale pre-training as a zero-shot forecaster)
- 这个方面关注模型的泛化能力和潜力。通过第4.4节的大规模预训练实验,作者展示了Timer-XL一旦经过海量数据预训练后,无需在下游任务上微调(即零样本),就能在未曾见过的数据集和任务上取得良好效果,这使其有成为“基础模型”的潜力。
- 评估TimeAttention的有效性和模型效率(Assessing the effectiveness and efficiency)
- 在第4.5节,作者专门分析了其核心创新TimeAttention机制的有效性(如可视化)和模型的计算效率。同时,在前三节的实验里,与其它模型的对比本身也包含了对TimeAttention有效性的评估(例如,对比通道独立与通道依赖的模型)。
4.1 单变量预测
4.2 多变量预测实验
输入长度是672,输出长度是96。将预测结果作为输入进行迭代预测,预测四个长度{96,192,336,720}
模型核心组件输入输出的理解
从公式3可以看到,每个patch token首先和
对于多维变量预测来说,整体流程是一样的。只不过3.2小节写的更加详细点。对于公式6来说,
和传统的注意力机制相比,核心差别
实验部分总结
图3:引言部分提到,只使用编码器的transformer在长上下文预测中可能会出现性能下降,而基于解码器的Transformer则可以缓解这个问题。
PatchTST是基于编码器的架构,
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
- 第一章第四段,Multivariate Next Token Prediction:指在时间序列预测任务中,同时建模多个变量之间的依赖关系,并基于当前和历史观测值,联合预测下一个时间步的多个变量值。
- 第三章Approach。对时序变量token的定义:
- 一个序列长度是TP,一个时序token被定义为P个连续的时间点,那么每个patch token的长度就是T。
- 序列长度=token数量*token长度。而P就是token长度。
- 不过这里我有个问题,就是在符号A(公式8)是不是和公式6里面提到的一样?如果是一样,干嘛非要拆成两个矩阵?直接计算不好吗,反正最后再外面要套一个Mask矩阵
实验复现
因为需要复现实验,需要先统计下做了哪些实验,每个实验是如何设置的。
代码网址:https://github.com/thuml/OpenLTM
数据集描述:https://github.com/thuml/OpenLTM/blob/main/figures/datasets.png
数据集描述: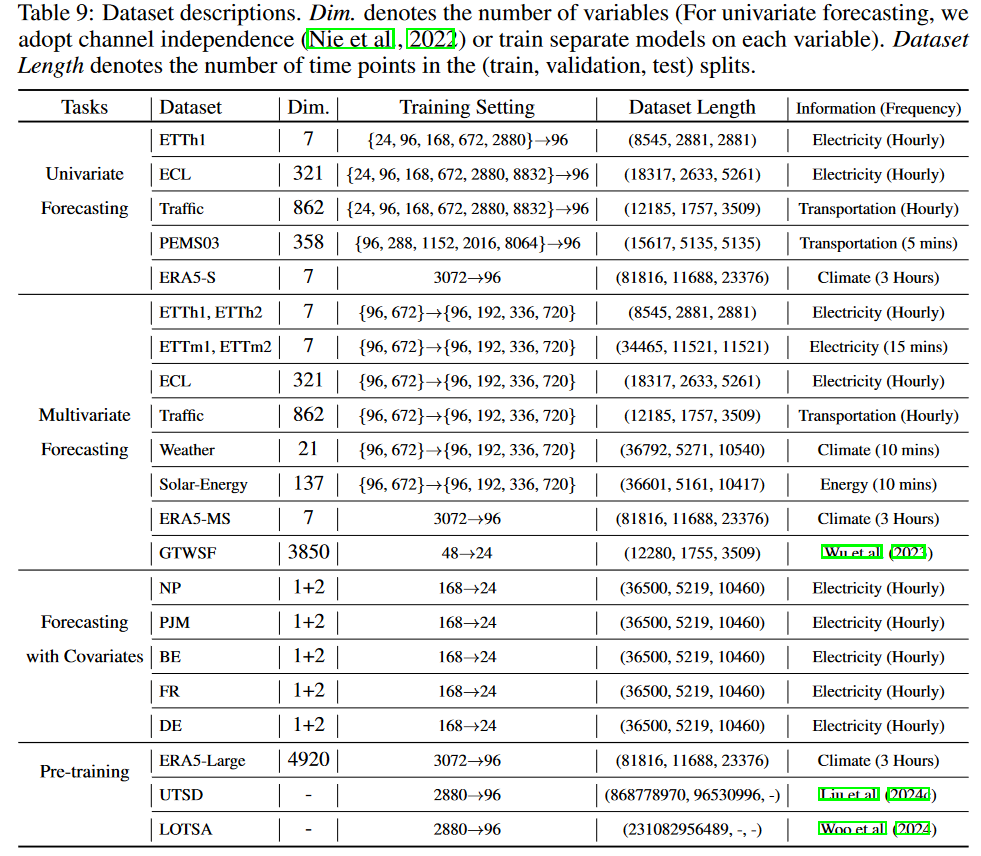
实验配置: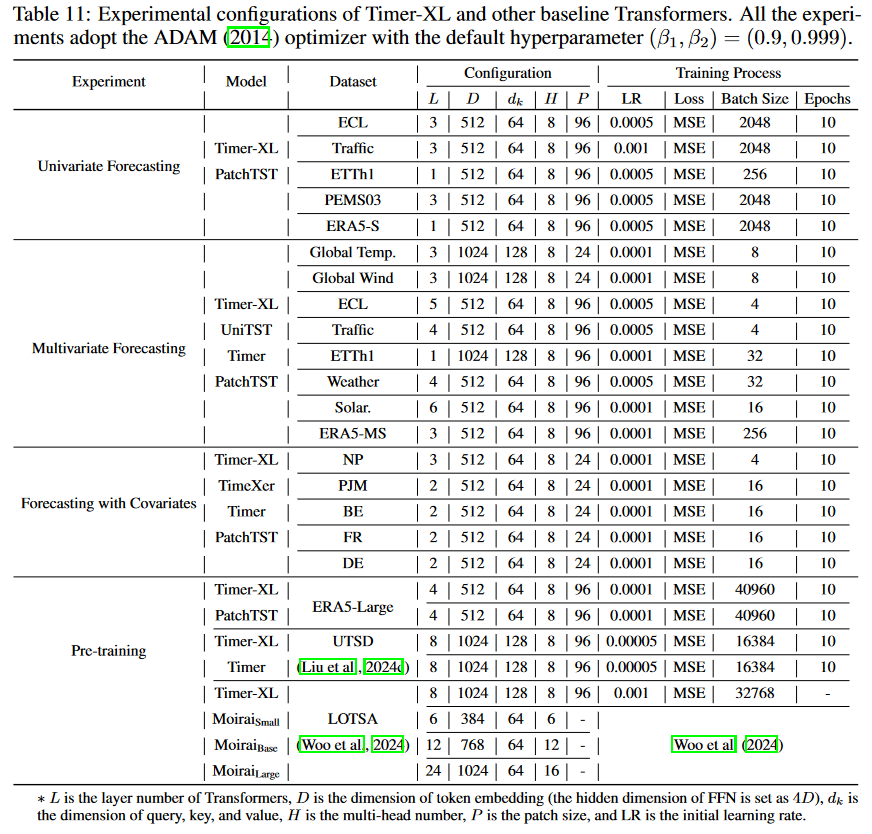
单变量时序预测
图3实验
实验步骤
- 预测的步长都是96。输入的数据长度不断增加,一共有5个不同的类型输入长度:1day(24步)、4day(96步)、1week(168步)、1month(672步)、4month(2880步)。我准备复制ETTh1这个数据集的结果。那么一共就是要进行5次实验,每次要修改输入的步长。每次的epoch为10次。
单变量时序预测采用多变量时序数据集要怎么处理
不过这里有个问题(已解决,在下一个点里面有提到),那就是论文在4.1中的Setups提到”Although these datasets are originally multivariate, they aim to be predicted in a univariate approach with the implementation of channel independence.”。这里我有些没看懂,因为图3的实验都是多变量数据集,但是实验却是单变量预测,那么选用哪个变量进行训练呢?论文没有说。但在附录B.3中提到“We adopt channel independence from Nie et al. (2022) in univariate time series forecasting.”。这个可能就是处理的方法,后面需要去看下这个论文是怎么做的。。关于上面的问题,有了回答。参考:https://zhuanlan.zhihu.com/p/602332939 。 所谓的channel independence就是对多变量分别进行预测,再将预测的结果拼接起来,这就相当于每个维度是独立的。
channel independence实验结果
代码里面连续三次验证集loss没有下降就早停。
- 输入步长24(1day):
- 第一次实验:epoch 5早停;mse:0.4135052263736725, mae:0.4306889474391937
- 第二次实验:epoch 5早停;mse:0.4135052263736725, mae:0.4306889474391937
- 第三次实验:epoch 5早停;mse:0.4135052263736725, mae:0.4306889474391937
平均效果:mse:0.4135052263736725, mae:0.4306889474391937
如果把data从MultivariateDatasetBenchmark换为UnivariateDatasetBenchmark,mse:0.37723585963249207, mae:0.3987869918346405
输入步长96(4day):
- 第一次实验:mse:0.3673262298107147, mae:0.3994017541408539
- 第二次实验:mse:0.3673262298107147, mae:0.3994017541408539
- 第三次实验:mse:0.3673262298107147, mae:0.3994017541408539
平均效果:mse:0.3673262298107147, mae:0.3994017541408539
如果把data从MultivariateDatasetBenchmark换为UnivariateDatasetBenchmark,mse:0.3619115948677063, mae:0.3970280587673187
输入步长168(1week):
- 第一次实验:epoch 9早停;mse:0.3750412166118622, mae:0.40709444880485535
后面两次结果也一样。
平均效果:mse:0.3750412166118622, mae:0.40709444880485535
替换后
mse:0.36265239119529724, mae:0.40084296464920044
- 输入步长672(1month):
- 第一次实验:epoch 6早停;mse:0.5115599036216736, mae:0.5127909183502197
- 第二次实验:epoch 6早停;mse:0.5115599036216736, mae:0.5127909183502197
- 第三次实验:epoch 6早停;mse:0.5115599036216736, mae:0.5127909183502197
平均效果:mse:0.5115599036216736, mae:0.5127909183502197
patch_size参数的默认值是16,在论文里面,这个值的设置是96,替换为96后,结果是一摸一样。epoch6早停,mse,mae一样。
如果把data从MultivariateDatasetBenchmark换为UnivariateDatasetBenchmark,在epoch4早停,mse:0.42560669779777527, mae:0.4508516490459442
输入步长2880:
多变量时序预测—table4
输入672步长,输出96。数据集ETTh1
论文结果:mse:0.409, mae:0.430
~~ 第一次结果:mse:0.7172967791557312, mae:0.6388883590698242。第二次一样。第三次结果一样~~
复现结果比较差,mse提高了75.3%;mae提高了48.6%
上面的结果有问题,因为是预测4个不同步长的结果,然后取平均,但是代码没有把4个结果取平均,而是单独输出,所以还需要自己计算下。计算后的结果:
mse:0.576475;mae:0.5523
后面又重新测试了下,发现mse和mae都变小了,这个把代码给贴上来,防止后面出现变化。
平均结果
mse: 0.5123112127184867825; mae: 0.5089017152786254875
export CUDA_VISIBLE_DEVICES=0
model_name=timer
token_num=7
token_len=672
# seq_len=$[$token_num*$token_len]
seq_len=$((token_num * token_len))
# training one model with a context length
# python -u run.py \
# --task_name singlegpuforecast \
# --is_training 1 \
# --root_path ./dataset/ETT-small/ \
# --data_path ETTh1.csv \
# --model_id ETTh1 \
# --model $model_name \
# --data MultivariateDatasetBenchmark \
# --seq_len $seq_len \
# --input_token_len $token_len \
# --output_token_len $token_len \
# --test_seq_len $seq_len \
# --test_pred_len 96 \
# --batch_size 32 \
# --learning_rate 0.0001 \
# --train_epochs 10 \
# --d_model 1024 \
# --d_ff 2048 \
# --gpu 0 \
# --lradj type1 \
# --use_norm \
# --e_layers 1 \
# --valid_last
# testing the model on all forecast lengths
for test_pred_len in 96 192 336 720
do
python -u run.py \
--task_name singlegpuforecast \
--is_training 0 \
--root_path ./dataset/ETT-small/ \
--data_path ETTh1.csv \
--model_id ETTh1 \
--model $model_name \
--data MultivariateDatasetBenchmark \
--seq_len $seq_len \
--input_token_len $token_len \
--output_token_len $token_len \
--test_seq_len $seq_len \
--test_pred_len $test_pred_len \
--batch_size 32 \
--learning_rate 0.0001 \
--train_epochs 10 \
--d_model 1024 \
--d_ff 2048 \
--gpu 0 \
--lradj type1 \
--use_norm \
--e_layers 1 \
--valid_last \
--test_dir singlegpuforecast_ETTh1_timer_MultivariateDatasetBenchmark_sl4704_it672_ot672_lr0.0001_bt32_wd0_el1_dm1024_dff2048_nh8_cosFalse_test_0
done输入672步长,输出96。数据集ECL
论文结果:mse:0.155, mae:0.246
复现结果:mse:0.17138800024986267, mae:0.27118179202079773
4个长度的预测结果:
mse:0.14015242457389832, mae:0.24011272192001343
mse:0.1517903357744217, mae:0.2513769268989563
mse:0.15890070796012878, mae:0.2604312002658844
mse:0.17138800024986267, mae:0.27118179202079773
平均结果:
mse:0.1555578671395778675
mae:0.255775660276412965
输入672步长,输出96。数据集Traffic
4个长度的预测结果:
mse:1.4108110666275024, mae:0.7981050610542297
mse:1.4211959838867188, mae:0.800054669380188
mse:1.4341756105422974, mae:0.8021271824836731
mse:1.4508225917816162, mae:0.8043699860572815
平均结果:
mse:1.4292513132095337
mae:0.801164224743843075
输入672步长,输出96。数据集Weather
4个长度的预测结果:
mse:0.17348450422286987, mae:0.23053230345249176
mse:0.22228124737739563, mae:0.2735917568206787
mse:0.27404284477233887, mae:0.31003275513648987
mse:0.3528522253036499, mae:0.3624463975429535
平均结果:
mse:0.2556652054190635675
mae:0.2941508032381534575
输入672步长,输出96。数据集Solar-Energy
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
论文引用部分梳理
第一段:之前的工作大多集中在长期预测(long-term forecasting)上。但可靠的预测是需要考虑上下文的内生变化和外生相关性来做出的。此外,预训练Trans的上下文长度决定了推理过程中输入和输出的最大长度。因此,长上下文Trans比段上下文Trans更通用。
第二段:目前时序领域的Trans在长上下文预测遇到了问题,时序Trans通常只能支持数百个token的上下文。这种情况,对单变量来说,短上下文输入导致对全球趋势的学习不足,难以解决现实世界时间序列中的非平稳性;对于多变量来说,捕获变量间和变量内部的关系是很有效的,这突出了扩展上下文长度以涵盖相互关联的时间序列的实际紧迫性。
这段指出了时序trans在长上下文预测中遇到的问题,并且说明这个问题如果不解决,会很麻烦,凸显长上下文预测的重要性。
第三段:为什么选择基于decoder的Trans来做这个工作
第四段:
- 将语言建模的训练目标推广到多变量下一个标记预测,实现了统一的时间序列预测,覆盖了单变量、多变量、协变量预测。
- 在纯解码器架构的基础上,提出了TimeAttention。
- 将上下文扩展到上千个patch tokens。并在单变量、多变量和协变量信息预测基准上达到了最先进的水平。
- 通过在大规模数据集上进行预训练,我们将 Timer-XL 作为Timer的超长版,Timer-XL在零点预测方面优于最近的大型模型。
三个方面的贡献:
- 提出了多变量下一个标记预测和统一的时间序列预测,通过扩大上下文来强化Transformers,从而做出信息完整的预测。
- TimeAttention。一种为多维时间序列量身定制的新型因果自关注。
- Timer-XL,能缓解长上下文时间序列中的性能下降,在特定任务基准测试中达到最先进的性能,并通过预训练实现显著的 “零镜头 “性能。
实验复现v2
Figure3—Univariate forecasting (pred-96) of well-acknowledged benchmarks under channel independence (Nie et al., 2022). We increase the lookback length to encompass monthly and yearly contexts.
- 实验描述:在4个不同数据集上面分别测试,单变量预测,预测长度是固定的,为96。输入长度不断增加。因为单变量数据集长度不够,我们采用了多变量数据集,通过通道独立实现单变量预测。
数据集:ETTh1
- 输入长度:24(1day),patch_size:3
- 输入长度:96(4day),patch_size:12
- 输入长度:168(1week),patch_size:24
- 输入长度:672(1month),patch_size:96
- 输入长度:2880(4month),patch_size:384
数据集:ECL
数据集:Traffic
数据集:PEMS03
Table3—Univariate forecasting (input-3072-pred-96) of ERA5-S, encompassing 117k time points in each station (40-years).
- 实验描述:
Are Transformers Effective for Time Series Forecasting?
- LTSF(long-term time series forecasting)
- DMS(direct multi-step)
- IMS(iterated multi-step)
2023-AAAI
Summary
作者质疑了LTST-Transformer在长时间时序预测中的有效性,通过与LTSF-linear的方法进行对比来验证猜想。
Transformer的核心是多头注意力机制,该机制在提取长序列中元素之间的语义关联方面有非常强的能力。但是注意力机制是具有permutation-invariant,会破坏时序中的order。为例验证这个想法,将LTSF-linear和LTST-Transformer方法进行比较,并进行以下实验:
- 注意力机制是否对LTSF有效
- 步骤:逐渐将Informer中的注意力层转换为线性层。
- 结论:随着模型越来越简化,性能也在不断提高。对这些模块的必要性提出质疑。
- 现有的LTST-Transformer能否较好的保留时间序列
- 步骤:通过两种方式破坏输入序列的原始顺序:Shuf. (Random Shuffle): 将整个输入序列的顺序完全随机打乱、Half-Ex. (Half Exchange): 将输入序列的前半部分和后半部分直接交换。这个实验应该是先把模型训练好,然后输入三种不同的序列(原始、shuf、half-ex),观察和原始的相比性能下降多少。如果原始的数据是周期性很强的数据,那么打乱后,性能应该会下降很多。并且周期性越强的数据,性能下降越多。
- 结论:
- Exchange数据集(周期性差):LTST-Transformer影响非常小;LTST-Linear效果很差,shuf后性能下降很明显。
- ETTh1数据集(周期性一般):FEDformer和Autoformer有“time series inductive bias”模块,导致性能下降很大;而Informer没有这个,性能下降的比较少。
- 论文说因为LTST-Linear的平均下降率要高于LTST-Transformer,所以LTST-Transformer的方法不能很好的保留时序。这个结论我觉得可以这样理解,因为是比较原始和打乱的差异,时序保留的越好,那么打乱后,效果就会越差。而LTST-Transformer的下降率要比LTST-Linear的低,说明它反而没有保留好时序。
- 不同embedding策略效果如何
- 要去了解下三个former的embedding策略,位置的和时间的。
- 训练数据大小对LTST-Transformer的影响
- 可以去看看清华那篇timer-xl,看看它的测试长度是多少,作者在这个地方的结论是弱结论。
- LTST-Transformer效率真的提升了吗
- 从表8可以看出来,和经典Transformer相比,大多数Transformer的变体在推理时间和参数上都差不多,甚至变差了。因为后面的这些变体引入了更多的设计,使得实际成本变得更高。
论文作者提到的核心贡献不在于提出了一个线性模型,而在于抛出了一个重要问题(Transformer在时序预测中真的有效吗),展示了令人惊讶的对比,并从不同角度证明了为什么 LTSF-Transformers 并不像这些著作中声称的那样有效。
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
- Transformer的核心是多头注意力机制,该机制在提取长序列中元素之间的语义关联方面有非常强的能力。
- 但是注意力机制是具有“排列不变性”的。排列不变性是指:在语义丰富的NLP任务中,如果我们把一个句子中部分词位置置换,再喂入Transformer学习,对point-wise自关注机制学习其语义信息并不会有太大的影响。这便是排列不变性。
- 排列不变性让模型只关注语义信息,而忽略时序顺序信息。但在时序数值数据中,order信息是非常重要的,并且很多时序数据(如股价、电价)是缺乏语义信息的,因此我们希望模型更关注连续点集,而不是离散点集,但实际上用point-wise的自注意力机制,应具有排列不变性,会导致过拟合时序噪声,而非真正时序信息,导致泛化性能差。
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?)
- 证明Transformer没有学习到时序信息
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
- 作者假设长时间预测仅仅对具有相对清晰的趋势和周期性的时序数据有用(introduction-5para),而线性模型已经可以提取此类信息。所以选用名为LTSF的模型为baseline,直接预测未来时间序列。
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
对比方法
基础base-line:
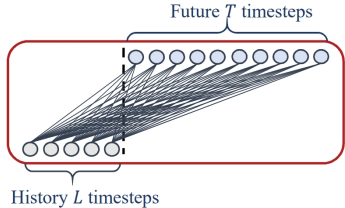
数学表达式为:。权重矩阵W的维度是T*L,T是预测窗口大小,L是输入窗口大小。 预测时间步1:
预测时间步2:
只要矩阵 W中每一行的权重值不同,即使输入序列相同,计算出的每个未来时间步的预测值也是不同的。 为了更好的处理不同领域的数据,在基础的LTSF-Linear基础上引入两个变体:
- DLinear: 将Autoformer和FEDformer中的”Decomposition“策略和线性层结合。首先通过移动平均核将原始数据输入分解为趋势成分和剩余(季节性)成分。然后,对每个分量应用两个单层线性层,将两个特征相加得出最终预测结果。
- NLinear: NLinear 首先用序列的最后一个值减去输入值。然后,输入经过一个线性层,再将减去的部分加回来,最后进行预测。NLinear 中的减法和加法是对输入序列的简单归一化。
- 四种Tranformer的变体:FEDformer、Autoformer、Informer、Pyraformer
- 原始的DMS方法:重复look-back窗口中的最后一个值
注意力机制是否对LTSF有效
- 逐渐将Informer中的内容转换为线性层。将注意力层转换为线性层,得到Att-Linear;摒弃Informer中的其他辅助设计(如FFN),只留下嵌入层和线性层,得到Embed+Linear。最后将模型简化为线性层。
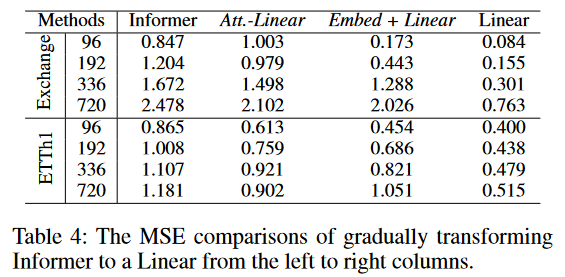
结论:随着模型越来越简化,性能也在不断提高。对这些模块的必要性提出质疑。
现有的LTSF-Transformer能较好的保留时间序列吗?
- 该实验旨在测试模型是否真正理解和依赖输入序列的时间顺序。它通过两种方式破坏输入序列的原始顺序:Shuf. (Random Shuffle): 将整个输入序列的顺序完全随机打乱、Half-Ex. (Half Exchange): 将输入序列的前半部分和后半部分直接交换。
- 如果模型严重依赖于正确的时间顺序,那么在这种顺序被破坏后,其性能(即MSE)应该会显著下降。
- “Average Drop”这一列量化了模型在顺序被破坏后,性能变差的程度。这个指标要分为Shuf和Half-Ex两部分来看。我们以FEDformer在ETTh1上的性能来看,一共有4个不同预测长度的结果,分别是0.753、0.730、0.736、0.720,这四个值分别和对应的Ori结果计算变化率,以第一个为例,(0.753-0.376)/0.376。然后把四个结果加起来除以4,就得到了“Average Drop”。这个结果正的越多,表面结果下降的越厉害;负的越多,表面性能还有提升。
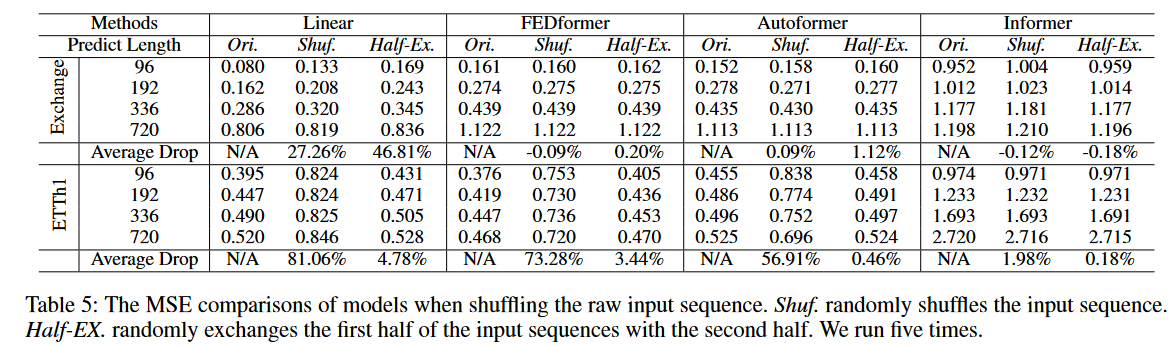
- 结论:
- 对于汇率数据集。所有的LTSF-Transformer方法性能变化很小,而LTSf-Linear的性能却大幅下降。这表明,具有不同位置嵌入和时间嵌入的LTSF-Transforme保留的时间关系相当有限,容易对有噪声的金融数据产生过拟合,而简单的 LTSF-Linear 可以自然地对顺序进行建模,并以较少的参数避免过拟合。
- 对于ETTh1数据集,FEDformer和Autoformer因为引入了”time series inductive bias“,使得能提取更具有周期性数据的特征。因此,在Shuf设置下,两个模型的性能下降很多。而Informer没有这种temporal inductive bias,效果反而下降的少。
不同嵌入策略的效果如何?
- 如果没有位置嵌入(wo/Pos.)如果没有时间戳嵌入(wo/Temp.),随着预测长度的增加,Informer 的性能也会逐渐下降。由于 Informer 对每个token只使用一个时间步长,因此有必要在每个token中引入时间信息。
- FEDformer 和 Autoformer 不在每个token中使用单一的时间步长,而是输入一系列时间戳来嵌入时间信息。因此,在没有固定位置嵌入的情况下,它们可以实现相当甚至更好的性能。
- 如果没有时间戳嵌入,Autoformer 的性能就会因为全局时间信息的丢失而迅速下降。
- 由于 FEDformer 中提出了频率增强模块来引入时间归纳偏差,因此它在移除任何位置/时间戳嵌入后受到的影响较小。
训练数据的大小是现有基于Transformer的LTSF方法的限制因素吗?
- 在训练数据减少的情况下,预测误差通常较小。这可能是因为与较长但不完整的数据规模相比,全年数据能保持更清晰的时间特征。
- 虽然我们不能得出结论说应该使用更少的数据进行训练,但这表明训练数据规模并不是限制性原因。
效率真的是最重要的因素吗?
- 现有的基于Transformer的LTSF方法声称原始Transformer的时间复杂度都是
,尽管他们进行了优化,理论上最高优化到了 ,但是还不清楚,实际的推理时间和内存消耗是否也优化了。
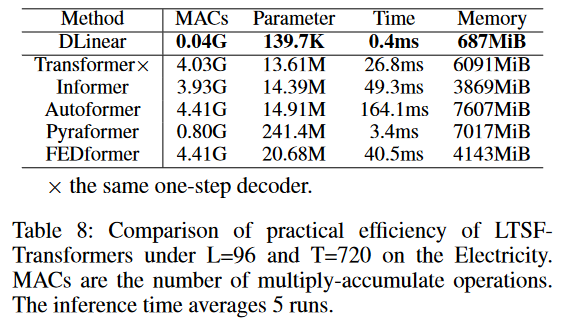
从表8可以看出来,和经典Transformer相比,大多数Transformer的变体在推理时间和参数上都差不多,甚至变差了。因为后面的这些变体引入了更多的设计,使得实际成本变得更高。
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
知乎评论有人提到,这篇论文是由漏洞的,找的实验用的数据集基本看不出周期性,EXchang数据真就完全没有啥周期性。ETT有点,但是不多。如果换成PEMS04这样的分布漂移不严重的数据,这些工作效果最好的就是Informer。(Are Transformers Effective for Time Series Forecasting? - 马东什么的文章 - 知乎
https://zhuanlan.zhihu.com/p/569194246)有一篇论文对这篇文章的论点进行了回应,发现了在时间序列上高效使用transformer的方式,效果超越DLinear和其他formers。见知乎评论:Transformer是否适合用于做非NLP领域的时间序列预测问题? - 科研汪老徐的回答 - 知乎
https://www.zhihu.com/question/493821601/answer/2506641761 。 论文名称:A Time Series is Worth 64 Words: Long-term Forecasting with Transformers
可以去验证下是不是这样
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
- AutoFormer、Informer、FEDformer、Pyraformer。这篇论文提到,Informer输入一系列时间戳来嵌入时间信息,在没有固定位置嵌入的情况下,效果也不错;AutoFormer提出了频率增强模块来引入时间归纳偏差,因此它在移除任何位置/时间戳嵌入后受到的影响较小。
Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting
[2021-NeurIPS]
下面这个图我基本是看懂了,包括Decoder部分的两个输入,Seasonal Init后面的Zero,就是表示拼接0,对应论文里面的公式2;而Trend-cyclical Init后面的Input DataMean也对应公式2。不过唯独Encoder Input那张图里面的“To Predict”我不知道是什么意思。我理解的是模型的预测结果拼接过来,那么这样不就变成了rolling吗,但是实验部分也没有强调这个。
我又看了下,这个“To Predict”应该表示的是预测长度,在论文第三章开头也有一个,“To Predict”表示的是一个变量,表示预测步长。但是每个步长应该要单独训练。
Summary
作者研究长时间时序预测问题。现有的研究局限主要有两点:(1)直接从长时间序列中挖掘时序依赖关系是很难的。传统的时序分析方法Decomposition只关注历史序列,忽略了未来序列和历史序列之间存在的依赖关系;(2)Transformer-based方法计算复杂度高。之前有人将使用稀疏注意力,但是point-wise这种方式只能捕获单个时间点之间的关系,无法捕捉序列之间的关系。
为了解决上述问题,作者提出了Autoformer,核心点为:
(1)Series decomposition block:为了学习长时间预测中的复杂时间模式,将时序数据分解为trend-cyclincal和seasonal两部分,反映了序列的长期变化特点和季节性变化特点。
(2)Auto-Correlation:挖掘序列中子序列之间的关联性。
模型架构:
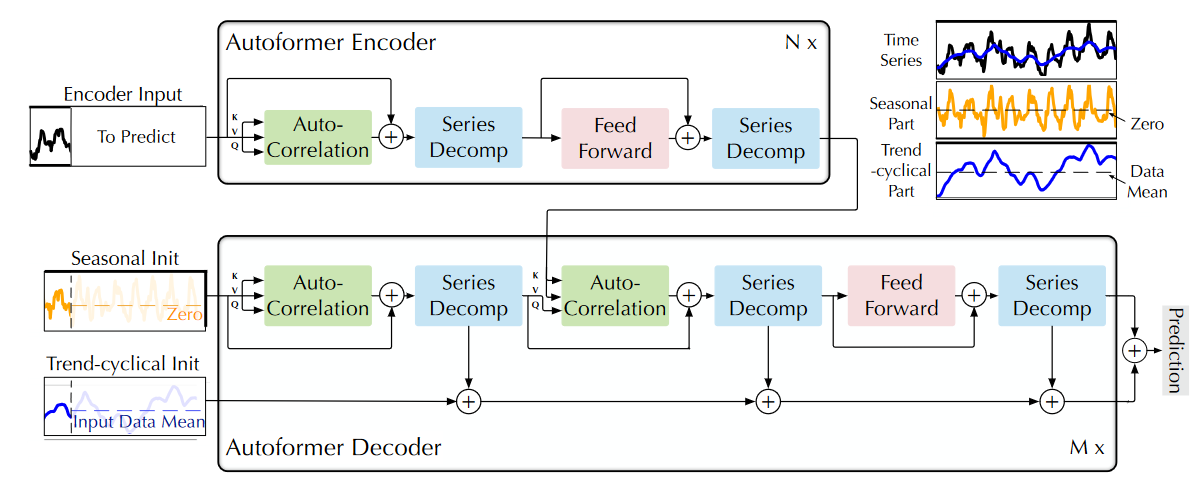
过去
Series decomposition block:
trend-cyclical:seasonal:
summarize above equations:
Model inpus:
- Encoder:Encoder的初始输入是过去
个时间步, 。Encoder部分的SeriesDecomp模块,会舍弃掉trend-cyclical,只关注seasonal part。 
- Decoder:
Decoder部分的初始输入是将Encoder后半部分时间步数据放入SeriesDecomp模块,得到和 ,再分别和零向量和 的平均值平均,得到Decoder的输入数据。 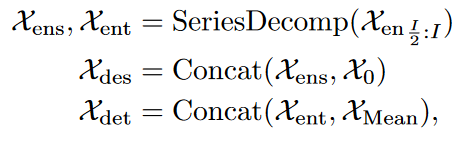
- Encoder:Encoder的初始输入是过去
Auto-Correlation:Auto-Correlation机制的工作流程主要包括两个步骤:Period-based dependencies和Time delay aggregation。
Period-based dependencies:自动找到时间序列中具有较强关联的子序列。具体做法是计算序列的自相关函数(Autocorrelation)。对于序列
,其与自身滞后 个时间步的序列 的相似性,通过自相关函数来衡量。函数值越高,说明这两个子序列之间具有较强的关联。自相关函数如下: 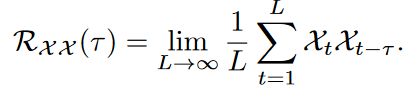
Time delay aggregation:对子序列的信息进行聚合。
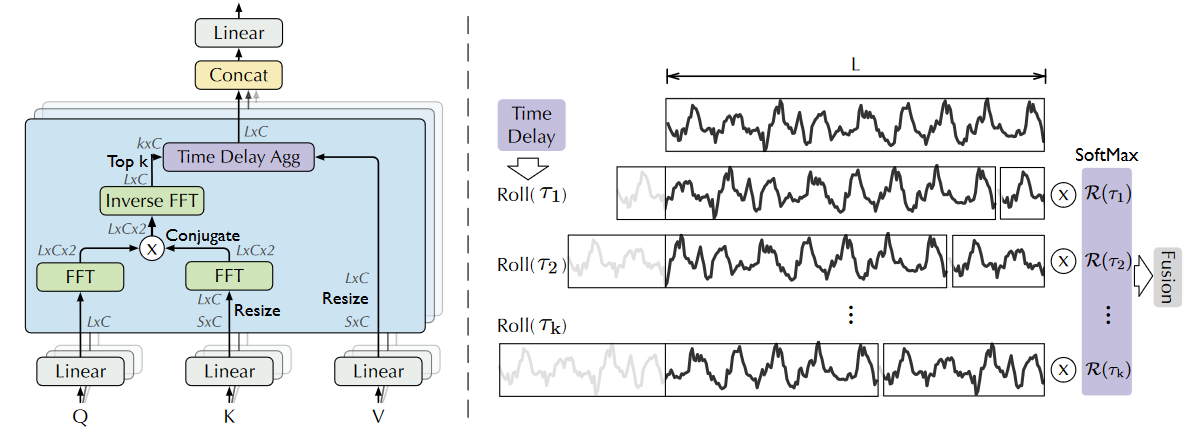
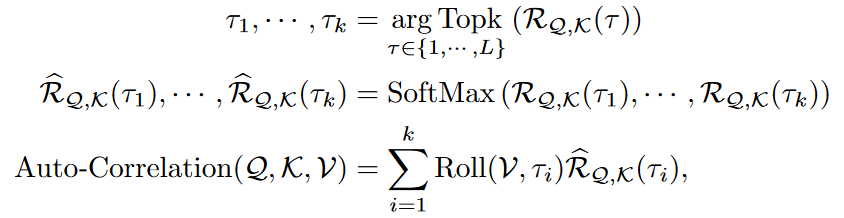
对
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
研究的动机和必要性:
- 时序预测广泛应用于能源消耗、交通和经济规划、天气和疾病传播预测等领域
- 迫切的需求就是将预测时间延长到更远的未来,这对于长期规划和预警来说意义重大。
现有研究局限:
- 直接从长期时间序列中发现时间依赖关系是不可靠的,因为依赖关系可能会被纠缠(entangled)的时间模式所掩盖。
- 典型的Transformer-based方法计算复杂度高,之前有方法将注意力改为稀疏注意力,但是使用了point-wise representation aggregation。会因为稀疏的point-wise而牺牲信息利用率,从而造成时间序列长期预测的瓶颈。
解决这些局限的研究挑战:
- 为了对错综复杂的时间模式进行推理,我们尝试采用分解的思想,这是时间序列分析中的一种标准方法。它可以用来处理复杂的时间序列,提取出更多可预测的成分。由于未来是未知的,Decomposition只能用作过去序列的预处理。这种常见的用法限制了分解的能力,忽略了被分解成分之间未来潜在的相互作用。
论文方法的出发点和解决思路:
- 基于时序分解方法,并试图超越分解的预处理用法。使深度预测模型具备渐进分解的内在能力。此外,分解还能揭示纠缠不清的时间模式,突出时间序列的固有特性[15]。得益于此,我们尝试利用序列的周期性翻新自我关注中的点-线联系。我们观察到,各周期中处于同一相位的子序列往往呈现出相似的时间过程。因此,我们尝试根据序列周期性得出的过程相似性来构建序列级连接。
论文方法的主要技术方案:
- Auto-Correlation:在序列层面发现依赖关系并进行信息聚合。根据序列的周期性发现子序列的相似性,并从基础周期中汇总相似的子序列。对于长度为 L 的序列,这种系列机制的复杂度为 O(L log L),并通过将点表示聚合扩展到子序列级别。我们的机制超越了以往的自相关系列,可同时提高计算效率和信息利用率。
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?这部分可以从Introduction最后一段的contributions中去找,贡献对应的就是解决了什么问题)
Decomposition这种预处理方法受限于历史序列的简单分解效应,忽略了未来长期序列基本模式之间的层次互动关系。
典型的Transformer-based方法计算复杂度高,之前有方法将注意力改为稀疏注意力,但是使用了point-wise representation aggregation。会因为稀疏的point-wise而牺牲信息利用率,从而造成时间序列长期预测的瓶颈。
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
- 针对问题1:从一个新的渐进维度引入分解思想。我们的 Autoformer 将分解作为深度模型的内部模块,可以在整个预测过程中逐步分解隐藏序列,包括过去序列和预测的中间结果。
- 针对问题2:Auto-Correlation:在序列层面发现依赖关系并进行信息聚合。根据序列的周期性发现子序列的相似性,并从基础周期中汇总相似的子序列。对于长度为 L 的序列,这种系列机制的复杂度为 O(L log L),并通过将点表示聚合扩展到子序列级别。我们的机制超越了以往的自相关系列,可同时提高计算效率和信息利用率。
Decomposition Architecture:
- Series decomposition block:
- 这部分的操作主要是将原始的数据进行分解,得到趋势-周期和季节两部分数据。具体的操作见公式1,这个过程被概括为
。对应图1中的“Series Decomp”模块
- 这部分的操作主要是将原始的数据进行分解,得到趋势-周期和季节两部分数据。具体的操作见公式1,这个过程被概括为
- Model inputs:
- encoder输入:过去
个时间步, - decoder输入:包含趋势-周期和季节性两部分呢输入,两部分输入的维度是待定,都是
- 每次输入
- encoder输入:过去
- Encoder:
:因为Encoder部分有两个Series Decomp模块,这里面的上标 表示第几个Series Decomp模块的输出。
- Decoder:
- 分为两部分:趋势-周期成分的累计结构;季节成分的叠加自相关结构。
- 每个Decoder部分都包含inner Auto-Correlation和encoder-decoder Auto-Correlation。其中encoder-decoder Auto-Correlation应该就是Decoder部分中间的Auto-Correlation模块,这个模块的k和v是来自Encoder。分别完善预测和利用过去的季节性信息。
- Decoder整体流程分为三个部分,两个Auto-Correlation+Series Decomp,再接一个Feed Forward+Series Decomp。
Auto-Correlation Mechanism:
1. 设计动机:
传统Transformer模型采用点对点(Point-wise) 的自注意力机制,这种方法在长序列预测中存在明显局限:- 计算效率低
- 信息利用瓶颈:点对点的关联方式难以有效捕捉时间序列中固有的子序列级(Sub-series level) 的周期性模式。
Auto-Correlation机制的工作流程主要包括两个步骤:基于周期的依赖关系发现和时延聚合。
2. 基于周期的依赖关系:
这一步的目标是自动找到时间序列中隐藏的周期长度。具体做法是计算序列的自相关函数(Autocorrelation)。- 自相关函数:对于序列 {X_t},其与自身滞后τ个时间步的序列 {X{t-τ}} 的相似性,通过自相关函数 R{XX}(τ) 来衡量。R_{XX}(τ) 的值越高,说明该滞后时间τ所代表的周期长度可能性越大。
- 快速计算:论文利用维纳-辛钦定理,通过快速傅里叶变换(FFT)来高效计算所有可能滞后(τ from 1 to L)的自相关值,将复杂度降至 O(L log L)。
- 选择关键周期:算法并非使用所有周期,而是选取自相关值最高的k个时延τ₁, τ₂, …, τₖ(其中 k = ⌊c × log L⌋,c为超参数)。这些τ值即为模型识别出的最主要周期长度,其对应的R(τ)值作为聚合时的权重(置信度)。
3. 时延聚合:
这一步的目的是基于发现的周期,将不同周期中相似相位(即相同位置)的子序列信息进行聚合。- 滚动操作(Roll):对于每一个选定的关键时延τ_i,对值(Value)序列执行Roll(X, τ_i)操作。这个操作将序列整体向后滚动τ_i个时间步,使得当前时刻的相位与τ_i个时间步前的相位对齐。
- 加权聚合:最后,将所有经过滚动对齐的子序列,根据其自相关值R(τ_i)(经过Softmax归一化)进行加权求和,得到最终的聚合表示。
4. 高效计算:
在效率上,得益于FFT和仅聚合O(log L)个子序列,整个Auto-Correlation机制的时间复杂度和空间复杂度均保持在 O(L log L),使其能够高效处理长序列。5. 与Self-Attention家族的对比:
Figure 3 清晰地展示了Auto-Correlation与各种自注意力机制的本质区别:- (a)全注意力:所有点之间进行两两连接,计算开销大。
- (b)稀疏注意力(如Informer, Reformer):基于某种度量选择部分关键点进行连接,仍是点对点。
- (c)Log稀疏注意力:按指数间隔选择点进行连接。
- (d)Auto-Correlation:根本性地将依赖发现和信息聚合从点级提升到了子序列级。它基于序列的周期性,建立的是序列与序列(Series-wise) 之间的连接。
这种根本性的改变,使得Auto-Correlation在长时序预测任务中,同时兼顾了计算效率和信息利用的有效性,突破了传统点对点自注意力的瓶颈。
- 6. 自相关计算参考资料
相关的概念可以参考这两个网站:https://zhuanlan.zhihu.com/p/583185155、https://zhuanlan.zhihu.com/p/430503143
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
消融实验
Table3
- 目的:验证论文所提出架构的有效性
- 操作:把论文提出的progressive architecture架构应用到其他模型,验证相比原模型是否有提高。这个就是表3中的Ours;在应用了架构后,分别训练两个模型,一个模型接收pre-decomposed seasonal的输入,并对其预测。另一个接收trend-cyclical components作为输出输出,最后将两个结果以某种方式合并。
Table4
- 目的:验证论文所提出注意力机制的有效性
- 操作:将Autoformer中的Auto-Correlation分别替换为其他注意力机制,例如:Full Attention、LogSparse Attention、LSH Att、ProbSparse Att。各种输入长度的效果都是最好的,并且部分方法还会内存溢出。
模型分析
这部分几乎没看懂,不知道它画的图到底想表达什么。等今天下午或明天再重新看下。
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
- 文中的idea是基于Decomposition方法,后面可以去了解下,参考文献是[1, 27]
第三章节中的Encoder部分,提到“the encoder focuses on the seasonal part modeling”。没有明白为什么重点是季节部分,而不是趋势-周期?(这个问题已经弄明白了)- 4.3小节中的模型分析。我不太理解Seasonal Part和Trend-cyclical具体应该是什么样?比如说,一个时序数据被分解为seasonal和trend,那么应该是什么样,后面可以让ai给我写一个简单程序看一下。(这部分具体的内容,可能需要结合代码才能看懂,或者跑一下实验才行)
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting
Summary
- 论文5.5小节专门回答FEDformer和Autoformer的区别,因为这两个架构非常像。
- 作者认为 Autoformer 本质上是将序列分解为多个时域(Time Domain)子序列来进行特征提取,其傅里叶方法仅用于加速子序列相似度的计算 。
- 相比之下,FEDformer 使用频率变换将序列分解为多个频域(Frequency Domain)模式来提取特征 。它不再进行局部的子序列选择,而是从整个序列(Whole Sequence)中计算全局频率特征,从而获得更好的长序列预测性能
- 这篇论文和Autoformer都是没有使用归一化的,而归一化的那篇论文叫《REVERSIBLE INSTANCE NORMALIZATION FOR ACCURATE TIME-SERIES FORECASTING AGAINST DISTRIBUTION SHIFT》,可以去看看
- 这篇论文的核心模块是Frequency Enchanced Block(FEB)和 Frequency Enhanced Attention(FEA)具有相同的流程:频域投影 -> 采样 -> 学习 -> 频域补全 -> 投影回时域:
- 首先将原始时域上的输入序列投影到频域。
- 再在频域上进行随机采样。这样做的好处在于极大地降低了输入向量的长度进而降低了计算复杂度,然而这种采样对输入的信息一定是有损的。但实验证明,这种损失对最终的精度影响不大。因为一般信号在频域上相对时域更加“稀疏”。且在高频部分的大量信息是所谓“噪音”,这些“噪音”在时间序列预测问题上往往是可以舍弃的,因为“噪音”往往代表随机产生的部分因而无法预测。相比之下,在图像领域,高频部分的“噪音”可能代表的是图片细节反而不能忽略。
- 在学习阶段,FEB 采用一个全联接层 R 作为可学习的参数。而 FEA 则将来自编码器和解码器的信号进行cross-attention操作,以达到将两部分信号的内在关系进行学习的目的。
- 频域补全过程与第2步频域采样相对,为了使得信号能够还原回原始的长度,需要对第2步采样未被采到的频率点补零。
- 投影回时域,因为第4步的补全操作,投影回频域的信号和之前的输入信号维度完全一致。
这里面有个地方要说明下,那就是第3不中提到的”用一个全联接层 R 作为可学习的参数“,从图上看,这个参数R和
低秩近似(low-rank approximation):
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
研究的动机和必要性:
现有研究局限:
解决这些局限的研究挑战:
论文方法的出发点和解决思路:
论文方法的主要技术方案:
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?这部分可以从Introduction最后一段的contributions中去找,贡献对应的就是解决了什么问题)
Transformer-based方法计算成本高,无法捕捉从全局视野捕捉时序特征。
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
idea从两个方面来
- seasonal-trend分解。虽然已经有人把这个思想用到了transformer-based方法,但是我们根据Kologrov-Smirnov 分布检验,我们提出了一种特殊的网络设计,它能有效地使预测的分布接近ground-truth的分布。
- 傅里叶变化。fft与trans结合,应用于频域而不是时域。应用于频域能帮助trans捕捉时序的全局属性。
FEDformer的一个关键问题是:应该选择哪些频率来表示时序?通常的观点是保留低频,过滤高频,但这可能不适用用时序。因为时序中的某些变化trend变化和important events相关,简单的去除高频成分,可能会丢掉这部分信息。根据理论分析,随机选择频率成分(低频和高频)能为时序提供更好的表示。实验也验证了这一点。
将Trans与频域分析结合,除了能更有效的进行长期预测,还能降低计算复杂度,这个和以往的trans不一样(应该是指linear trans之类的),这类trans会一定程度牺牲性能。
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
A TIME SERIES IS WORTH 64 WORDS: LONG-TERM FORECASTING WITH TRANSFORMERS
ICLR 2023
Summary
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
- 研究的动机和必要性:
预测是时序分析中最重要的任务之一。深度学习在预测任务中表现的很好,深度学习中非常有代表性的工作则是Transformer。但是最近的一篇论文(Are Transformers Effective for Time Series Forecasting?)表明线性模型在各种常见时序数据集上的性能都要优于Transformer。
- 现有研究局限:
解决这些局限的研究挑战:
论文方法的出发点和解决思路:
论文方法的主要技术方案:
论文提出一种与通道无关的补丁时间序列变换器(PatchTST)模型来回答这个问题。关键设计点有两个 :
- Patching:时序预测旨在了解不同时间步中数据的关联性。单个时间不像语句中的单词那样具有语义,因此提取局部语义信息对分析他们之间的连续是很重要的。大多数研究只使用point-wise输入token或者只从序列中手工提取信息。相比之下,我们通过将时间步数聚合成子序列级的片段,增强了局部性,并捕捉到了点级所不具备的全面语义信息。(感觉和autoformer说的很像,思路也非常相似)
Channel-independence:多变量时序数据就是一个多channel的信号。Transformer的token可以是来自单通道,也可以是多通道。channel-mixing表示就是表示后者。Channel-independence已经在CNN(Zheng 等人,2014 年)和线性模型(Zeng 等人,2022 年)中被证明效果良好,但尚未应用于基于 Transformer 的模型。
和之前的模型相比,论文模型有以下几个优点:
- 减少时间和空间复杂度:不经过预处理,input token会和序列长度L相同。通过Patching,把N设置为L/S,然后还有patch length P(我理解的是,序列总长度是L,先划分为多个子序列,就是L/S。然后在每个子序列里面划分patch,每个patch的长度就是P)
- 从更长的look-back窗口中学习的能力:
- 表征学习的能力:证明Transformer在时序预测中的有效性,并且效果要优于Dlinear模型。
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?这部分可以从Introduction最后一段的contributions中去找,贡献对应的就是解决了什么问题)
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
- Forward Process: 假设输入look-back window:
。时间长度是L,一共有M个变量。对于每个单变量来说,维度是 。每个单变量都单独的输入模型中 - Patching:这个过程是这样的。每个单变量是
,patch的时候先确定每个patch的长度 ,然后采用滑动窗口的形式进行分割,滑动的步长是 ,然后根据公式 ,得到有多少个patch,也就是说每个单变量会被划分为多少个patch,然后把这些patch拼接起来,就得到了 。
- Instance Normalization:这种技术最近被提出来帮助减轻训练数据和测试数据之间的分布偏移效应。它简单地将每个时间序列实例 x(i) 归一化为零均值和单位标准差。实质上,我们在修补之前对每个 x(i) 进行归一化处理,然后将均值和偏差加回输出预测中。
表征学习
用PatchTST来获取多变量时序数据中的有用表征。
自监督学习中,掩码autoencoder是很流行的。目前应用与时序,在分类和回归任务中取得了显著的性能。掩码被用在每个时间序列或者不同的序列,但是这样做有两个问题:
- 在单个时间步层面应用掩码。当前时间步的掩码,可以通过后续的时间值推断出来,不需要对整个序列有高水平的理解。偏离了我们学习整个序列的重要抽象表示的目标。
- 传统Transformer在预测任务输出层上有设计缺陷,会导致参数巨大,容易过拟合,计算和内存开销也大:
- 假设输入回溯序列长度 L = 336, Transformer隐藏层维度 D = 128, 要预测的变量数 M = 10, 预测长度 T = 96。输入进入隐藏层后,会变为新的表示向量 z ∈ R^(L×D) = R^(336×128);最终得到的预测结果维度是 R^(M×T) = R^(10×96)。为了实现这种映射,需要一个线性层(全连接层),其权重矩阵 W的维度为 (L·D) × (M·T)。在这个例子中,就是 (336 128) × (10 96) = 43008 × 960。这个矩阵包含超过 4千万个参数。
- 使用PatchTST可以有效的解决这个问题:输入是Patch,不是单时间点: 模型首先将长度为L的序列分割成N个长度为P的Patch。例如,L=336, P=16, S=8,则 N ≈ (336-16)/8 + 2 = 42个Patch。patch进入隐藏层后,z^{(i)} ∈ R^(D×N)。这里的N(如42)远小于原始的L(336)。模型最终需要预测的是未来T个具体时间点的值。因此,需要将N个Patch的抽象特征 z^{(i)}转换回T个时间点的预测。这是通过一个Flatten层 + 线性投影头实现的:
- Flatten: 将 z^{(i)} ∈ R^(D×N)展平为一个长向量,维度为 D*N。
- 线性投影: 用一个较小的线性层将这个 DN维的向量直接映射到 T维的输出(对于单变量序列)。这个线性层的权重矩阵维度仅为 (DN) × T。沿用上面的例子,就是 (128 * 42) × 96 = 5376 × 96,参数数量约51.6万,比传统方法的4千万参数减少了两个数量级
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
长时间预测
- Transformer-based Models:
- FEDformer (Zhou et al., 2022): 使用傅里叶增强结构来降低复杂度。
- Autoformer (Wu et al., 2021): 结合了分解和自相关机制。
- Informer (Zhou et al., 2021): 提出了ProbSparse注意力机制和蒸馏技术
- Pyraformer (Liu et al., 2022): 采用金字塔式注意力模块。
- LogTrans (Li et al., 2019): 使用卷积自注意力和LogSparse设计。
- Non-Transformer Model:
- DLinear (Zeng et al., 2022): 一个简单的线性模型,其论文结论对Transformer在时间序列预测中的有效性提出了挑战。
- 输入与输出设置 (Input/Output Settings)
- 输入长度 (Look-back window, L):
- 对于大多数Transformer基线模型,默认的回看窗口为 L = 96。
- 对于DLinear模型,默认 L = 336。
- 为了确保基线模型的表现不被低估,作者对FEDformer、Autoformer和Informer额外测试了多种回看窗口 L ∈ {24, 48, 96, 192, 336, 720},并选取其最佳结果作为最终对比,这使得基线非常强大。
- 预测长度 (Prediction horizon, T):
- 对于ILI数据集:T ∈ {24, 36, 48, 60}
- 对于其他所有数据集:T ∈ {96, 192, 336, 720}
- 评估指标: 使用均方误差 (MSE) 和平均绝对误差 (MAE) 作为评估模型预测准确性的标准。
- 输入长度 (Look-back window, L):
- PatchTST模型变体 (Model Variants)
作者提出了两个版本的PatchTST模型以进行公平和探索性的比较:- PatchTST/42: 使用默认回看窗口 L=336,通过分块(Patch长度 P=16, 步长 S=8)后产生 N=42个输入令牌。此设置用于与基线模型(如DLinear)进行公平对比。
- PatchTST/64: 使用更长的回看窗口 L=512,产生 N=64个输入令牌。此设置用于探索模型在更大数据集上的潜力,追求更好的性能。
实验结果:
实验结果表明,PatchTST模型在绝大多数情况下都显著优于所有基线模型。
整体性能领先:
- 与Transformer基线模型的最佳结果相比:
- PatchTST/64 在MSE上整体降低了 21.0%,在MAE上整体降低了 16.7%。
- PatchTST/42 在MSE上整体降低了 20.2%,在MAE上整体降低了 16.4%。
- 与DLinear模型相比,PatchTST同样展现出优势,尤其是在大规模数据集(Weather, Traffic, Electricity)和ILI数据集上表现更为突出。
关键结果分析:
- 该总结性表格清晰地展示了PatchTST在不同数据集和不同预测长度下的全面领先优势。其性能提升是显著且一致的。
- 结果有力地回应了DLinear论文的挑战,证明了通过恰当的设计(分块和通道独立),Transformer架构在时间序列预测任务中不仅是有效的,而且是极其强大的。
Representation Learning
本节的核心目的是证明PatchTST模型不仅在有监督学习中表现卓越,在自监督表示学习领域同样能取得 state-of-the-art (SOTA) 的性能,并具备强大的迁移学习(Transfer Learning) 能力。
Table4
为了公平且全面地评估自监督预训练的价值。它通过对比三种不同的模型训练策略来实现这一点:
- sup:Supervised。模型(PatchTST)直接在目标数据集(如Weather, Traffic)的带标签数据(即已知的历史和未来数据对)上训练至收敛
- Lin.Prob:模型首先在无标签数据(只使用历史数据,不涉及未来数据)上进行掩码预训练。然后,在进行下游预测任务时,冻结(固定) 预训练好的Transformer编码器的所有权重,只新训练一个简单的线性输出层(Linear Head)。
- Fine-tuning:先应用线性探测 10 个历时来更新模型头,然后对整个网络进行 20 个历时的端到端微调。事实证明,先线性探测后微调的两步策略优于直接进行微调的策略。
结论:仅进行线性探测(Linear Probing) 的结果就已经可以媲美甚至超越从零开始训练(Supervised from scratch) 的PatchTST模型以及强大的DLinear模型。这雄辩地证明了预训练编码器提取的特征质量极高,无需调整其权重就足以完成准确的预测。意味着我们可以通过大规模无标签数据预训练一个通用的“时间序列基础模型”,然后在具体任务上只需训练一个轻量的线性头,从而大大降低下游任务的计算成本和数据需求。
Table6
在ETTh1数据集上,无论是使用自身数据预训练(Self-supervised)还是从Traffic数据集迁移过来(Transferred),PatchTST(仅用线性探测)的性能都大幅领先于所有对比学习方法(TS2Vec, BTSF, TNC, TS-TCC)。
消融实验
本节的核心目的是通过一系列控制变量实验,确凿地验证PatchTST模型中两个核心设计——分块(Patching) 和通道独立(Channel-Independence)——各自的有效性与必要性,并探究其他因素(如回看窗口长度)的影响。
- Table7:核心组件消融:分块(P)与通道独立(CI)
- Figure2: 回看窗口长度(Look-back Window L)的影响
- 原则上,较长的回视窗口会增加感受野,从而有可能提高预测性能。随着回看窗口L的增大,PatchTST的性能(MSE)持续稳定地提升。相比之下,FEDformer、Autoformer和Informer等基线模型的性能在L超过某个值后无法进一步提升,甚至可能下降。这表明这些模型缺乏有效利用长历史信息的能力。证明我们的模型有能力从更长的回视窗口中学习。
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
论文里面提到Patching的优势有两个:
- 同样的显存可以运行更多数据,达到训练加速的目的。
- 传统的trans-based方法捕捉的是单一时间点的依赖,但是单一时间点不具备类似自然语言中的语义。Patching可以捕捉局部范围时间的依赖,具有类似自然语言中的语义。
下面来解释下这两点,关于Trans计算复杂度的相关知识可以看《Transoformer》那篇博客。
Trans的计算复杂度
假设原始输入是(256,336,1).batch_size为256;输入长度为336,变量数为1。然后会进入embedding层,那么维度会变为:
如果使用patch,假设没有重叠切割,分为21个块,每个块长度为16。PatchTST的embedding层仍然会进行线性映射,维度还是512,得到的结果是
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
WAVENET: A GENERATIVE MODEL FOR RAW AUDIO
论文是做音频生成的,核心共享:
- 可以生成具有主观自然度的原始语音信号
- 为了处理长时间依赖性,开发了基于扩张因果卷积的新架构,该架构表现出非常大的感受野。
Dilated Causal Convolution
因果卷积说白了就是掩码卷积,和因果注意力一样的道理。
不过好处就是不受限于循环连接,可以并行训练,训练速度比RNN快。
对于卷积来说,有个问题就是,如果卷积核太小,那么感受野就小,模型能学习到的特征就很有限,因为只能看到局部的,长距离的场景下,可能就无法保持连贯性。理论上来说可以使用一个大核卷积来解决这个问题,但是大核卷积可能会导致参数量过大,而且模型可能无法获得非线性能力。这里举个例子:
方案 A:直接用一个巨大的卷积核(你的设想)
如果只用一层卷积,要达到 16,000 的感受野,卷积核大小必须等于 16,000。 参数量公式:
计算:
结果:参数量与感受野成线性比例增长。方案 B:WaveNet 的空洞卷积堆叠(Dilated Convolution)
WaveNet 使用卷积核大小,通过指数级增加的 Dilation ( ) 来扩大感受野 1。
要达到 16,000 的感受野,大约需要 14 层(因为)。 参数量公式:
( 为层数)
计算:结果:参数量与感受野的对数( )成比例。
最关键的其实还是非线性表达能力,这里要多说一句和它相关的,也就是大部分模型是先升维再降维:
https://www.zhihu.com/question/1956421703728076399/answer/1956810843154019269
https://www.zhihu.com/question/1956421703728076399/answer/1956436758561551971
升维并不是凭空增加信息,而是把原始数据映射到更高维的表征空间,让模型能更容易地分离复杂模式、表达特征交互,并容纳更多参数来提升表达能力。就像在低维空间难以分开的点,到了高维就可能变得线性可分,升维的作用更多是扩展可分性和表达力。
降维则是对冗余和噪声的压缩,把高维表征里最核心的结构和模式抽取出来,既提高了计算效率,又增强了抽象能力。它不是简单地丢信息,而是通过压缩获得更浓缩、更有意义的表征。
换句话说,升维是扩展探索空间,降维是提炼有效信息,交替进行,构成了深度学习表征学习的过程。
An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling
解决了什么问题
Sequence Models之前主要聚焦在(recurrent)循环架构上。有些研究表明,某些卷积架构在音频合成、机器翻译方面达到SOTA,那么引出一个问题:卷积序列建模是否只限于特定领域,或者是否对序列处理和循环架构之间的关系进行重新考虑?
做了什么事
提出了一个适用所有任务的通用序列建模架构(TCN)。
方法
核心特点:
- 卷积是因果的
- 支持任意输入和输出长度
- 如何使用深度网络和扩张卷积来获得long effective history size(我个人的理解就是记忆能力)
MODERNTCN: A MODERN PURE CONVOLUTION STRUCTURE FOR GENERAL TIME SERIES ANALYSIS
Adaptive Multi-Scale Decomposition Framework for Time Series Forecasting
时序在不同的采样模式上表现出不同的时间模式。
解决了什么问题
trans-based在长序列方面能较好的建模,但是有以下问题:
(1)计算复杂度高、训练效率慢
(2)在长序列中提取语义关系的时候会削弱时间关系。会导致过度强调突变点,导致过拟合。
idea
MLP-based,计算复杂度低,可以按照时间序列建模,
挑战
然而,现有的基于 MLP 的方法中线性映射的简单性带来了信息瓶颈(Liu 等 2024b),阻碍了它们捕捉不同时序的能力
方案
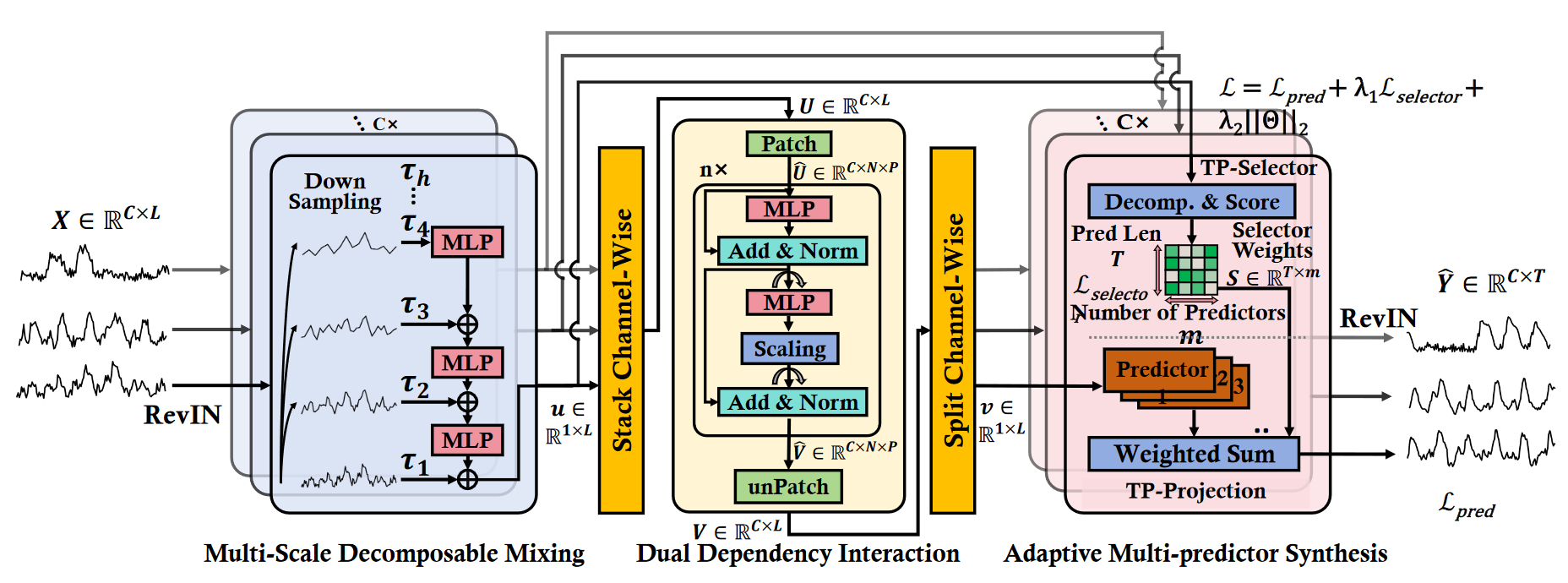
提出了一个基于 MLP 的自适应多尺度分解(AMD)框架,以更好地分解时间序列中的不同时间模式并为其建模。
Multi-Scale Decomposition Mixing Block(MDM)
采用channel-independence,对每个变量单独进行操作。
最终得到的是:通过池化对每个变量进行多个尺度的聚合,丰富了每个变量的信息。
首先是通过池化得到不同粗粒度(回应论文的出发点,不同采用频率表现出不同的时间模式)的数据。具体来说:
假设我们有一个长度
第一层:
数据:[10, 20, 15, 25, 30, 40, 35, 45]
第二层:
操作:在
[15, 20, 35, 40]
以此类推。
然后对池化的结果进行聚合,具体来说:
每个通道会得到多个
Dual Dependency Interaction Block(DDI)
这一层首先会对上一步中各个通道的数据给堆叠起来。然后按照变量维度和时间维度进行patch,然后以patch为单位来聚合特征。
来自 MDM 模块的
然后是切片操作,将长度为
然后DDI模块是由n个模块堆叠成的,这个块包含两个子层,分别处理时间和通道依赖。
时间依赖(针对每个变量内部的patch进行特征提取):
通道依赖:
为了让 MLP 能处理“变量”维度,需要对矩阵进行转置,把
将 MLP 的输出乘以一个可学习或预设的参数
最后将处理后的通道特征加回原来的
。
经过
Adaptive Multi-predictor Synthesis Block(AMS)
思想:对预测有重大影响的时间模式在不同时期会发生变化,有更强的预测能力。TimeMixer仅仅使用平均聚合,我们利用MOE的自适应特性,为每种时间模式设计特定的预测器,动态分配更多注意力给主要的时间模式,以此提高预测的准确性。
最终的输出结果是公式9的加权和:
(1)权重由TP-Select部分成:输入是MDM模块的输出,根据公式8、7和10对前top-k个主时间模式赋予一个值,对后top-k个模式赋予另一个值(公式10)。
(2)被加权的输入是由TP-Projection部分生成:输入是DDI模块的输出,每个变量单独操作,最后再拼接。每个变量输入进入专家网络,专家网络的权重由TP-Select来控制。
实验部分
消融实验
- MDM:对多个尺度进行聚合。
- 验证思路:去除这个模块;
- 结果:单一尺度不足以进行准确预测。
- DDI:捕捉变量内部和变量之间的依赖关系,缩放率是用来平衡对时间相关性和跨信道相关性的重视。
- 验证思路:去除这个模块、调整缩放率;
- 结果:缩放率可以平衡多元时间序列数据中对时间依赖性和跨渠道依赖性的重视,并提高模型的性能。
- AMD:根据MDM的输出结果,对前top-k个权重和后top-k的个权重进行区分;基于权重,使用MOR,对DDI的结果进行聚合。
- 验证思路:
- RandomOrder:没有使用 MDM 输出的真实
(包含时序特征的 embedding)作为输入来生成权重,而是将其替换为了随机的序列/向量。(这个是问的gemini,有可能不正确,我也不是很理解这个意思) - Average Weight:每个专家的权重是一样的。原文采用的是TP-Selector 的动态打分机制(Softmax/Top-K 等)
- RandomOrder:没有使用 MDM 输出的真实
- 验证思路:
Notes
这篇论文比较复杂,感觉像多个部件拼凑起来的,超参数也多。具体来说:
(1)架构复杂。主要有三个模块,从时间粗细粒度、时间/变量维度等进行多次特征提取。然后再经过复杂的加权方式来聚合。
(2)超参数多:公式6,7,8,10都有超参数
(3)损失函数由三个部分组成,而且损失函数里面还有两个超参数。
Revitalizing Multivariate Time Series Forecasting: Learnable Decomposition with Inter-Series Dependencies and Intra-Series Variations Modeling
2024[ICML]
Summary
假设我们的输入是(32,7,96)。表示每个batch_size是32,变量数是7,输入长度是96。
RevIN是很对每个样本里面的每个变量进行处理。也就是说,同一个样本里面的同一个变量一共有96个时间点,对这96个时间点计算均值方差,然后归一化。
而batchnorm,是针对每个变量处理,也就是同一个变量,要处理样本时间点(3296)个数据点,进行归一化。
Background
(研究的背景,帮助你理解研究的动机和必要性,包括行业现状和之前研究的局限性。)
研究的动机和必要性:
现有研究局限:
解决这些局限的研究挑战:
论文方法的出发点和解决思路:
论文方法的主要技术方案:
Problem Statement
(问题陈述:问题作者需要解决的问题是什么?这部分可以从Introduction最后一段的contributions中去找,贡献对应的就是解决了什么问题)
Method(s)
(作者解决问题的方法/算法是什么?是否基于前人的方法?基于了哪些?)
Evaluation
(作者如何评估自己的方法?实验的setup是什么样的?感兴趣实验数据和结果有哪些?有没有问题或者可以借鉴的地方?)
Conclusion
(作者给出了哪些结论?哪些是strong conclusions, 哪些又是weak的conclusions。即作者并没有通过实验提供evidence,只在discussion中提到;或实验的数据并没有给出充分的evidence?)
Notes(optional)
(不在以上列表中,但需要特别记录的笔记。)
References(optional)
(列出相关性高的文献,以便之后可以继续track下去。)
待整理的问题(主要是关于时序异常检测相关的东西)
时序内容总结:
- 复现模型,效果很差。
原文:
作者:john
链接:https://www.zhihu.com/question/1302007972/answer/22655276244
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
手头工作需要复现patchtst,所以对他的代码做了重建,结论是:这都什么鬼。。。如果说patchtst还算效果不错,那么其他xxformer简直就是xxx引子是一个本源的问题:transformer effective in TS?patchtst的作者给出答案是正面的,可是我想说,patchtst的模型设定,本质也就是个linear模型,transformer几乎没贡献。来看看patchtst的几个dataset,weather,traffic,illness,exchange_reate,electricity,ett-small。除了个别频率到了30分钟和15分钟,其他都是1hour。patch length是16(supervised,with stride=8) /12(self-supervised,with stride=12),所以作者认为数据集里面日内的波动都不重要?不需要用transformer来model?CV里面有一开始就用整个图片一半大小的卷积核来提取特征的吗?还是nlp里直接将文章段落tokenize?OK你说重点是model日间的波动和趋势,那为什么要用小时频率的数据,而不是降频使用每日的数据?一旦用每日数据,look-back window在相同input length情况下岂不是可以更长?所以patchtst,以及其他ts领域xxformer关于缩短input 序列长度的努力可能都有问题。用高频数据但是很大的patch size和stride,等于将高频波动交给了linear(或者卷积),对于日期级别的数据而言input length可能又不够patchtst还有一个创新,channel independent,这个我觉得就是偷懒。以traffic数据集为例,北京东三环的交通流量,跟西北五环的交通流量,能有什么关联?各个路口之间其实更多是一种graph的关系,稍微用点图神经网络的先验知识也能得到更好的建模结果吧?总结:transformer在ts的研究还很粗糙,虽然有端到端的需求,但是任何先验知识都不利用的建模,很可能得到跟linear差不多的结果补充吐槽一句:xxformer 的作者们受国外zzzq那套东西影响,学术也这么搞,根本不管时序的固有特征,只是琢磨:transformer如何处理更长序列,transformer如何节约显存,如何减少训练时间。。。调个sota 发顶会,名利皆丰
评论1:
这一系列最恶心的是,评价指标都是在标准化的结果上测的,都没有还原回来
这一系列工作,最大的亮点就是归一化了评价指标,大家对比mse,mae就好了,要画图的话分分钟露馅
原来你们早就发现了,实际业务落地,moving average is all you need
预测跟ground truth对比环节,到了复杂时间序列的部分,画个图一看,xxxformer就是lag 1输出,大亮[捂脸] MSE MAE这些指标能不是最优的嘛 直接成朴素预测法了
评论2:
patchtst效果好的原因是因为时间序列里每个点之间基本没啥关系,而且噪音很大,注意力机制很难提取到东西,或者说注意力的噪音比收益大。patchtst加上patch操作以后自注意力机制变成了1D卷积,所以效果好。事实证明时间序列数据太过简单,但根据点的值完全无法提取信息,有的注意力机制可以提取是因为他们是面向位置的注意力而不是面向变量值的注意力。
- 时序任务的本质
“和图像、语言相比,时间序列不是一种数据类型,而是一种数据格式”
意思是说不同领域的时序数据的特性可能完全不相同,只不过统一在时序这个格式下?
而且因为时序数据的在不同领域的巨大鸿沟,导致不能形成有效的统一预测大模型,原始数据必须经过挖掘
3.时序预测不要进入
强烈不建议有志之士进入时序预测领域,几乎所有的时序预测方法和paper都是伪科学,已有方法work前提条件往往要求系统趋于稳态可控,但这往往与实际不符,反过来看,如果已知系统趋于稳态了,写规则或者任意xx网络 都可以work。[赞同]
4.
LTSF的根本问题
有没有发现,所有LTSF文章,它的任务范围是超级通用的,气候、交通、能源、心电信号、汇率这些领域,都在暗示它有用。然而,这几个任务是不同的,气候和心电明显是确定性动力系统,而汇率是随机动力系统,甚至到了random walk的地步(知乎上有大佬介绍了Bergmeir的批评),这要求你的模型,既能搞确定性动力系统,又能搞随机动力系统,甚至还要对付non-stationarity,out-of-distribution。
当然,在现实世界数据中,难以预测的数据经常三样都粘:比如陷入一个局部混沌的区域,一些随机的known unknowns,和一些直接改变分布的冲击(真正的unknown unknowns),可能都会发生。所以,这个超级通用的任务设定,我姑且认为勉强合理。
但是!给这些LTSF模型的任务又是超级困难的。当我们用绩点,GPA来考核学生的时候,“绩点”这两个字就已经默认了这个学生是大学生;当你用MSE考核预测的时候,你默认的东西可太多了:
默认1:每个点都是可预测的(真正的pointwise predictability)。很多人喜欢预测的股价,和Bergmeir大佬批评的exchange rate 这个数据集都很类似random walk。random walk你可以算期望,方差,但是下一个点你是预测不了的,唯一能做的就是用上一个点预测下一个点。我看有评论区说某某former都是用昨天的价格预测明天的价格,嗯,会不会是你喂了太随机的数据呢?很可能人家收敛到了最合理的策略,反而说明了这模型是真的有东西。另外,混沌系统是没法预测的,最著名的就是蝴蝶效应的Lorenz系统,他的每一步的轨迹永不相交也永不重复,不但长期预测是根本不可能,短期预测的话每一步数据提供给你的信息都不带重样的。那什么东西可以用MSE预测?最简单的,比如说统计/计量101教的回归:线性DGP(data generating process,数据生成机制)加上一个独立常方差高斯噪声(aka Homoscedasticity / 同方差性,逆天的幽默经济术语,说人话叫 Constant variance Gaussian noise)。这种情况下 MIN MSE = MAX MLE,用线性回归测的就是最优线性无偏估计量(Best Linear Unbiased Estimator)。
默认2:我只在乎每个点的表现。早一点,晚一点,都不行,错就是错。如果实际数据是[1,2,3,…10],而我预测的是[2,3,4,5…11],评委不会考虑我结构上的正确性,只是看到每个点你都错了。但其实,我们真的需要那么准确么?股票的话,我看个大概趋势不行么?我的趋势错开了一段时间,算是真的错了吗?但是用MSE/MAE就意味着,这些都不重要,就是那么自信。这是用MSE/MAE来评判(evaluate)的问题。用它来做训练目标(training objective)那问题就更多了,最基本的,用MSE 训练代表要匹配条件概率的期望(expectation of conditional probability),意思是只要平均对了,剩下的无所谓。如果实际数据是[0,0,0]的话,预测[1,3,5]和[5,3,1]都是错,但是人类看来是有区别的吧?正负值很重要吧,尤其是炒股票的,[-1,3,-5]是不是又不一样了?
我们经常说能力越大,责任越大,拿transformer去测时序,它的灵活性和表现能力(expressiveness)比线性回归强多了。进去一团点云,因为模型的灵活性,出来也很可能是一团点云。如果数据是上上下下,很可能灵活的模型就会拙劣的模仿,(如果是train with MSE, eval with MSE的情况下),最后给你一团平均正确的点云就完事了。归根结底,这其实是模型能力和任务的不匹配,太灵活的模型碰上太随机的数据。
一个感想:
作为研究者,别去卷那几个benchmark。我个人建议,找一个简单的混沌系统去测验,为什么呢,因为(1)难度很大(真正长距离预测是不可能的,但是短期能测试模型性能)。(2)你知道每个数字的真正答案。统计学一个重要的法则,就是凡事先“play with toy set”,先在已知的数学结构上做实验,看看你这个模型能不能达标。记得别搞什么normalization。(3)所谓的“真实世界”数据集,很大程度上退化成了模拟器比赛,谁能模拟真实轨迹的平均数谁厉害,但是你并不知道“真实世界”的内在机制。只要模型在benchmark和PatchTST或者以上的模型打的有来有回,我觉得就不差了。很多人(比如曾经的我)怎么也跑不出来那种工整的sota,什么全数据,全长度,把baseline按在地上打,然后误以为自己的模型不行。另外,像weather这种数据集,偷偷藏了个-9999,不是知乎上有人提醒我都不知道,能跑的过DLinear才有鬼了。
结论:时间序列预测的极限远未触及,但突破的关键可能在于我们先要打破自己设定的思维牢笼——那些看似通用实则矛盾的评估标准和验证方式。
细节知识
rfft
时序预测中,傅里叶变化是使用比较多的,对应到代码里面来说,就是rfft。rfft 指的是 “实数快速傅里叶变换(Real FFT),输出的结果是复数(包含振幅和相位信息)
为什么叫”r”fft?因为实数信号的频谱具有“共轭对称性”(Hermitian symmetry),即正频率和负频率的信息是冗余的。rfft 专门利用这一点,只计算并返回一半的频率分量以节省计算量,但返回的每一个点依然是标准的复数(包含实部和虚部)。
所以如果输入的序列长度是720,那么使用rfft得到的数据量只有361。



