CFD知识

CFD

发布日期: 2024-03-03

文章字数: 8.2k

阅读时长: 31 分

阅读次数:

名词解释

weno3、weno5

在计算流体动力学（CFD）中，WENO，全称为加权基本非振荡器（Weighted Essentially Non-Oscillatory），是一种被广泛应用的数值方法，主要用于解决对流主导的流体动力学问题。

WENO方法的主要特点是能够在光滑区域中实现高阶精度，同时在激波和不连续性附近保持非振荡的解。这是通过对一组不同的预测子方案（即预测子 stencil）进行非线性加权来实现的，每个预测子方案对应于不同的插值多项式。

“WENO3”和“WENO5”指的是WENO方法的不同变体，数字表示用于构造预测子方案的插值多项式的阶数。例如，WENO3表示使用二阶插值多项式，而WENO5表示使用四阶插值多项式。理论上，WENO5在光滑区域的精度高于WENO3，但是在激波和不连续性附近，WENO5和WENO3的性能差距就不那么明显了。

CFD基础知识

网格计算

在计算流体动力学（CFD）中，网格（也称为网格点或计算网格）是用于空间离散化的基础，它将连续的流体域划分为一系列的离散单元或控制体。在这些网格点或网格单元上进行计算是CFD模拟的核心过程，这使得我们能够通过求解流体流动和传热等控制方程来模拟和预测流场行为。以下是对CFD计算中在网格点上进行计算的基本理解：

网格划分
网格类型：根据不同的需求，可以选择结构化网格、非结构化网格或混合网格。结构化网格通常是规则的、具有固定拓扑结构的网格，易于生成和计算；非结构化网格更加灵活，适用于复杂的几何形状。
网格密度：网格的密度（即网格点的数量和分布）直接影响计算的精度和计算成本。在流体流动的关键区域（如边界层、尾迹区等），通常需要更细的网格以捕捉流动细节。
控制方程离散化
方程离散化：连续的流体控制方程（如Navier-Stokes方程）需要通过离散化过程转换为一组可以在计算机上求解的代数方程。常用的离散化方法包括有限差分法（FDM）、有限体积法（FVM）和有限元法（FEM）。
计算过程：在每个网格点或网格单元上，通过求解离散化后的方程来计算流体的物理量（如速度、压力、温度等）。这些计算通常涉及网格点之间的相互作用，以及与边界条件的关系。
边界条件处理
边界条件：在CFD计算中，必须在域的边界上施加适当的边界条件，这些条件对流场的计算至关重要。边界条件可以是速度、压力、温度的已知值，也可以是更复杂的条件，如周期性边界、对称性边界等。
在网格点上的应用：边界条件直接施加于位于或靠近边界的网格点上，这些条件将在求解过程中被用来计算边界附近的流场行为。
迭代求解与收敛
迭代求解：对于非线性和耦合的方程组，CFD计算通常需要通过迭代方法求解。在每次迭代中，所有网格点上的物理量都会根据当前的流场状态和相互作用进行更新。
收敛判定：通过监控残差和关键物理量的变化来判断求解过程是否收敛。当这些量的变化降至某个预定的阈值以下时，可以认为已经达到了收敛状态，此时的网格点上的物理量代表了流场的最终解。

总结
在CFD计算中，网格点上的计算是通过将连续的流体控制方程离散化，然后在这些离散的点上求解这些方程来实现的。这个过程包括网格的划分、方程的离散化、边界条件的施加、以及通过迭代求解直至收敛的整个计算流程。正确的网格划分和高效的求解策略是获得准确可靠CFD模拟结果的关键。

收敛

在计算流体动力学（CFD）中，”收敛”是指通过迭代求解过程，计算得到的流场参数（如速度、压力等）随着迭代次数增加，趋于稳定的一个状态，不再发生显著变化。收敛是衡量CFD模拟是否成功达到预期物理状态的关键指标之一。在CFD模拟中，判断一个计算是否收敛，通常依据以下几个方面：

残差
残差是指实际流场参数与计算流场参数之间的误差。在迭代过程中，求解器会计算各个方程的残差，这些残差应当随着迭代次数的增加而减小。当残差降低到某个预定的阈值以下时，可以认为求解过程已经收敛。残差的阈值取决于具体的应用和精度要求，常见的阈值包括e-3、e-4等
物理量的变化
除了监视残差之外，还需要检查关键物理量（如速度、压力、温度等）随迭代次数的变化。如果这些物理量在连续几个迭代步骤中的变化非常小，那么可以认为求解过程已经收敛。具体的变化阈值同样依据实际应用和精度要求而定。
监视点或监视面
在CFD模拟中，可以设置特定的监视点或监视面，用来跟踪特定位置或区域内物理量随迭代过程的变化。如果这些监视点或监视面上的物理量变化趋于稳定，那么也可以作为收敛的一个判断依据。
流场特征
对于一些特定的流动问题，还可以通过观察流场的特征来判断模拟是否收敛，比如流线的分布、涡量的生成和消散等。如果流场的这些特征在连续几个迭代步骤中保持稳定，那么可以认为求解过程接近收敛。
综合判断
实际上，判断CFD模拟是否收敛通常需要综合考虑以上几个方面。单一指标可能不足以准确反映整个流场的收敛状态，尤其是在处理复杂流动问题时。因此，进行综合判断是非常重要的。

收敛后该做什么？
当CFD模拟最终收敛后，这意味着已经得到了一个稳定的流场解，这时候主要的工作转向结果的分析和验证，以及基于这些结果的后续应用。以下是一些在模拟收敛后可以进行的主要活动：

结果分析
流场特征分析：对流场中的速度、压力、温度等物理量进行详细分析，识别流动特征，如涡流、分离流、回流等。
性能评估：对于工程应用，根据流场分析结果评估产品的性能，例如，对于汽车外流场分析，评估空气阻力系数；对于管道流动，评估压降和流量分配等。
验证与验证（V&V）
验证（Verification）：确认数值解的正确性，即检查计算过程是否无误，包括网格独立性分析、数值方法的正确性等。
验证（Validation）：通过实验数据或其他可信来源的数据来验证模拟结果的物理准确性。
参数研究与优化设计
参数敏感性分析：通过改变关键参数（如入口流速、温度、几何形状等）来研究它们对流场和性能的影响，为设计提供依据。
设计优化：基于CFD结果，利用优化算法寻找最佳设计参数，以改善性能、降低成本等。
多学科耦合分析
结合结构力学、热传递、化学反应等其他物理过程的模拟，进行更为复杂的多物理场耦合分析，以更全面地评估和优化产品性能。

双时间步法

在计算流体力学中，采用双时间步法（Dual Time Stepping）处理非定常问题是一种常见的技术，尤其适用于处理复杂的瞬态流动。这种方法的核心思想是引入一个人工的“假”时间维度来加速收敛到每一个物理时间步的解，即在物理时间步固定的情况下，通过迭代解决一个或多个假时间步来求解非定常方程。这里的“定长”的意思是，在计算过程中，物理时间步保持固定，而在这个固定的物理时间步内部，使用多个假时间步来迭代求解。

工作原理

物理时间步：这是真实的时间步进，反映了流场随时间的实际变化。
假时间步：为了在每个物理时间步获得稳定和准确的解，引入一个额外的时间维度（称为假时间）。在每个固定的物理时间步内，通过多次迭代假时间来求解流场，直到达到某种收敛条件。这些迭代帮助稳定了求解过程，并确保了从一个物理时间步到下一个物理时间步的平滑过渡。

在双时间步法中，虽然处理的是非定常问题，物理时间步是固定的，即在每个物理时间点，计算条件并不改变，这样可以在每个物理时间步的计算中达到一种“定长”或稳定状态。在这种意义上，尽管整体问题是非定常的（随时间变化的），每个物理时间步的处理过程类似于求解一个定常问题，因为在达到物理时间步的解之前，假时间的迭代使得解在该物理时间点达到稳定。

应用场景

这种方法非常适用于需要时间精确性的流动问题，如不稳定流动、振荡流动等。通过在每个物理时间步内迭代假时间步，双时间步法可以有效地稳定数值解，并加快收敛速度，特别是在使用隐式时间离散化方案时。

定长&非定常

定长：

定常流动指的是流体流动的特性（如速度、压力等）在时间上不发生变化。这意味着即使流体在空间上的性质（如速度和压力）可能随位置变化，但在任何给定位置，这些性质随时间是恒定的。

非定常：

非定常流动指的是流体流动的特性在时间上有变化。在这种情况下，流体的速度、压力等参数不仅随空间位置变化，而且随时间也在变化。

区别

定常流动没有时间依赖性，而非定常流动具有时间依赖性。
通常，非定常流动的模拟比定常流动的模拟更为复杂和计算量更大，因为它需要解决流体特性随时间的变化，而定常流动只需考虑空间变化。
定常流动常用于工程设计和分析中相对简单或长期稳定的流动情况，而非定常流动则适用于研究流体动力学中的瞬态现象和时间变化效应。

数学知识

奇异值分解

奇异值分解（Singular Value Decomposition，简称SVD），可以用于矩阵的压缩和降维，通过保留最大的几个奇异值及其对应的奇异向量，可以近似原矩阵，这在图像压缩和数据降维等领域非常有用。在解决线性最小二乘问题、计算矩阵的伪逆等方面，奇异值分解也是一种非常重要的工具。

奇异值分解的计算一般通过数值算法实现，比如利用QR分解或者其他迭代方法，因为直接计算奇异值分解在数值上可能非常复杂。

下面讲解下奇异值分解的核心步骤：

1 收集数据集并构建数据矩阵

假设我们收集了个时刻的系统状态（例如流场数据），每个状态都是维的向量（例如流体的速度矢量和压力）。将这些数据组织成一个数据矩阵:

一般来说，N>>M。列通常被称为快照

2 执行奇异值分解（SVD）

U 是的单位正交矩阵，其列向量称为左奇异向量，代表数据的空间模式。

Σ 是的一个对角元素为非负值实数、非对角元素都为0的矩阵。对角元素被称为奇异值，由大到小排列。X的秩等于非0奇异值个数

V 是的单位正交矩阵，其列向量称为右奇异向量，代表时间模式。

如果X的列是依据时间获得的空间测量值，那么U对应空间模式，V对应时间模式。

奇异值分解和特征分解的联系

任何一个矩阵都可以进行奇异值分解，分解为，，三个矩阵

SVD的步骤一般就是两个：

求的特征向量（构成的矩阵就是V）和特征值（默认由大到小，对这个值求平凡根就是奇异值）
求的特征向量（构成的矩阵就是U）

和的特征值是一样的

基于POD的降阶模型(版本1：从左奇异向量U提取模态)

1 提取主要POD模态/模式

先执行前面的奇异值分解

选择r个最大的奇异值对应的左奇异向量，构成矩阵

构造模态系数

数据重构

是一个M*M的矩阵，但这个矩阵通常不是单位矩阵，除非选取了所有模态。所以不会直接消除。

误差来源：误差来源于中未包含的那些方向（即剩余的个方向）。这些方向可能包含较小的数据变化，但在某些情况下也可能含有重要信息。
近似质量：近似的质量依赖于的选择以及数据的本身特性。增加会改善近似的精确度，但同时会增加计算和存储的负担。

如果使用全部模态，当时，成为一个完整的正交基，覆盖了原始数据空间的所有维度。所以，是一个正交矩阵，满足以下条件：

上面说的重构是没有考虑数据去中心化的。如果是去中心化的，要在奇异值分解前减去平均值，重构的时候要加上平均值。看下面的代码：

def DimensionReductionOpt(S):
    #POD analysis
    # O = 3
    # pca = PCA(n_components=O)
    pca = PCA()
    coeff = pca.fit_transform(S.T)
    
    u_mean = pca.mean_.reshape(-1,1)
    u_modes = pca.components_.T
    a0 = coeff[-1] 
    
    #Optimization
    def Obj(a):
        u = u_mean + u_modes@(a.reshape(-1,1))
        # res通过读取resid_glb.out文件中的et_res来获取
        res = Res(u)
        obj = np.abs(res).mean()
        return obj
    # N*K = 100
    # outputs = minimize(Obj, a0, method='Nelder-Mead',tol=1e-16,options={'maxiter': int(N*K/10)})
    outputs = minimize(Obj, a0, method='Nelder-Mead',tol=1e-16,options={'maxiter': int(100/10)})
    u = u_mean + u_modes@(outputs.x.reshape(-1,1))
    return u

重构的代码就是u = u_mean + u_modes@(a.reshape(-1,1))

而投影在coeff = pca.fit_transform(S.T)就完成了，这个代码是自动进行了去中心化的，重构的时候要把平均值再加回去，所以上面的代码是没有问题的。

实现代码：

def perform_pod(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    # data shape :  (100, 2)

    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)

    print('pod U shape: ', U.shape)
    print('pod Sigma shape: ', Sigma.shape)
    print('pod VT shape: ', VT.shape)
    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前3个主要模态
    modes = U[:, :n_modes]

    print('pod modes shape: ', modes.shape)

    modal_coefficients = np.diag(Sigma[:n_modes]) @ VT[:n_modes, :]

    # 重构数据，使用所有模态
    reconstructed_data = np.dot(modes, modal_coefficients) + mean_data
    return reconstructed_data

基于POD的降阶模型(版本2，从右奇异向量V提取模态)

1 提取主要POD模态/模式

如果选择前K个模态，那么维度是

2 模态系数

模态系数：;如果选择前K个模态，那么维度是

实现代码：

def perform_pod_v(data):
    """执行POD并重构数据，使用SVD并选取V作为模态"""
    # 数据中心化
    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)
    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前2个主要模态
    modes = VT[:n_modes, :]  # 使用V的转置的前n_modes行

    print('pod_v modes shape: ', modes.shape)

    modal_coefficients = U[:, :n_modes] @ np.diag(Sigma[:n_modes])

    # 重构数据
    reconstructed_data = modal_coefficients @ modes + mean_data
    return reconstructed_data

pod的不同实现方式

pod的实现方式大体有两种，核心的关键在于矩阵的分解，用svd分解，还是传统的特征值分解。

下面我用代码来阐述下：

svd分解

def generate_data(n_time_steps):
    """生成一个简单的示例数据集"""
    t = np.linspace(0, 2 * np.pi, n_time_steps)
    data = np.array([np.sin(t), np.cos(t)]).T  # 2变量，n时间步
    print('data shape : ', data.shape)
    return t, data

def perform_pod(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化
    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)

    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前3个主要模态
    modes = U[:, :n_modes]
    modal_coefficients = np.diag(Sigma[:n_modes]) @ VT[:n_modes, :]

    # 重构数据，使用所有模态
    reconstructed_data = np.dot(modes, modal_coefficients) + mean_data
    return reconstructed_data

def perform_pod_pca(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    pca = PCA(n_components=2)
    coeff = pca.fit_transform(data)
    u_mean = pca.mean_.reshape(-1,1)
    u_modes = pca.components_.T

    reconstructed_data = u_mean + np.dot(u_modes, coeff.T)


    return reconstructed_data.T

上面的两个函数perform_pod_pca和perform_pod，你可以理解为一个详细版的，另一个是粗略版的。

关于pod的输入没有明确的规定，即样本数和特征数谁在前都是可以的，但是会对结果有些影响，但是不大。

gpt对此的解释是：

分析时间上的变化模式

如果你主要关注如何在不同时间点捕捉流场的变化模式，你可以将每个时间点的流场数据看作一个特征向量。m（样本数）：对应于时间点的数量，在你的案例中，这是10（你有10个不同时间点的流场数据）。n（特征数）：对应于每个时间点的数据点数量，在你的案例中，这是201（每个时间点有201个流场数据点）。
这样，每一行代表一个时间点的完整流场，列数则代表每个时间点被记录的流场数据点。

分析空间特征

如果你关注在所有时间点上各个特定空间位置的行为，你可能会选择将每个空间点的时间序列视为一个特征向量。m（样本数）：对应于空间点的数量，即201（每个时间点201个数据点）。
n（特征数）：对应于时间点的数量，即10（你有10个时间的流场数据）。
在这种情况下，每一行代表一个固定空间位置在所有记录时间点的流场变化。

特征分解

# 特征值分解
def perform_pod_eig(data):
    """执行POD并重构数据"""
    # 数据中心化
    mean_data = np.mean(data, axis=1).reshape(-1, 1)
    data_centered = data - mean_data
    
    # 构建协方差矩阵
    covariance_matrix = np.dot(data_centered, data_centered.T) / data_centered.shape[1]
    
    # 特征分解
    eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
    
    # 排序特征值和特征向量
    idx = eigenvalues.argsort()[::-1]
    eigenvalues = eigenvalues[idx]
    eigenvectors = eigenvectors[:, idx]
    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前3个主要模态
    modes = eigenvectors[:, :n_modes]
    modal_coefficients = np.dot(modes.T, data_centered)
    
    # 重构数据
    reconstructed_data = np.dot(modes, modal_coefficients) + mean_data
    return reconstructed_data

POD总结

不论输入矩阵的维度是 n m 还是 m n ，模态从U还是V中选择，最后重构出来的值都是一样的。

❗❗❗ 上面的回答是错的，如果把数据设置的复杂点，就会出现差异,只不过差异比较小

下面的代码可以直接运行，验证上面的回答：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

from sklearn.linear_model import LinearRegression

# 这个文件是为了确定模态是从左奇异向量还是右奇异向量里面获得的

def generate_data(n_time_steps):
    """生成一个简单的示例数据集"""
    t = np.linspace(0, 2 * np.pi, n_time_steps)
    data = np.array([np.sin(t), np.cos(t), np.cos(t)*np.sin(t)]).T  # 2变量，n时间步

    return t, data

def perform_pod_u(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    # data shape :  (100, 2)

    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)

    print('pod_u U shape: ', U.shape)
    print('pod_u Sigma shape: ', Sigma.shape)
    print('pod_u VT shape: ', VT.shape)
    
    # 提取前几个模态和模态系数
    n_modes = 20  # 选择前3个主要模态
    modes = U[:, :n_modes]

    print('u pod modes shape: ', modes.shape)

    modal_coefficients = np.diag(Sigma[:n_modes]) @ VT[:n_modes, :]

    print("pod_u modal_coefficients shape: ", modal_coefficients.shape)

    # 重构数据，使用所有模态
    reconstructed_data = np.dot(modes, modal_coefficients) + mean_data
    return reconstructed_data

def perform_pod_v(data):
    """执行POD并重构数据，使用SVD并选取V作为模态"""
    # 数据中心化
    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)
    
    # 提取前几个模态和模态系数
    n_modes = 20  # 选择前2个主要模态
    modes = VT[:n_modes, :]  # 使用V的转置的前n_modes行

    print('pod_v U shape: ', U.shape)
    print('pod_v Sigma shape: ', Sigma.shape)
    print('pod_v VT shape: ', VT.shape)

    print('v pod modes shape: ', modes.shape)
    modal_coefficients = U[:, :n_modes] @ np.diag(Sigma[:n_modes])

    print("pod_v modal_coefficients shape: ", modal_coefficients.shape)

    # 重构数据
    reconstructed_data = modal_coefficients @ modes + mean_data
    return reconstructed_data

def perform_pod_pca(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    # pca = PCA(n_components=2)
    pca = PCA(n_components=20)
    coeff = pca.fit_transform(data)
    u_mean = pca.mean_.reshape(-1,1)
    u_modes = pca.components_.T
    
    print('u_mean: ', u_mean.shape)
    
    print('u_modes: ', u_modes.shape)
    
    print('coeff: ', coeff.shape)

    reconstructed_data = u_mean + np.dot(u_modes, coeff.T)


    return reconstructed_data.T

def compare_arrays(arr1, arr2):
    """比较两个numpy数组的统计差异"""
    if arr1.shape != arr2.shape:
        raise ValueError("Arrays must have the same dimensions")
    
    # 计算差异数组
    difference = arr1 - arr2

    # 计算平均值差异
    mean_difference = np.mean(difference)
    
    # 计算最大值和最小值差异
    max_difference = np.max(difference)
    min_difference = np.min(difference)
    
    # 输出结果
    print("Mean Difference:", mean_difference)
    print("Max Difference:", max_difference)
    print("Min Difference:", min_difference)

# 生成数据
n_time_steps = 100
t, data = generate_data(n_time_steps)

data = np.random.rand(20,10000)

# data = data.T

print('data shape: ', data.shape)

reconstructed_data0 = perform_pod_u(data)

# reconstructed_data1 = perform_pod_v(data)
reconstructed_data1 = perform_pod_u(data.T)

reconstructed_data2 = perform_pod_pca(data)

compare_arrays(reconstructed_data1.T, reconstructed_data0)

代码中：

U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)

如果full_matrices=False，返回的U和V是经济尺寸，仅仅包含有意义的奇异值信息。

假设X是M*N

U的形状：M min(M,N)
V的形状：N min(M,N)

代码中：

u_modes = pca.components_.T

形状和V一样，说明默认选择的模态是从右奇异矩阵V里面选择的。

下面的一段代码是可以运行的，涉及pod三种不同的代码写法。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

from sklearn.linear_model import LinearRegression

# 这个文件是为了确定模态是从左奇异向量还是右奇异向量里面获得的

def generate_data(n_time_steps):
    """生成一个简单的示例数据集"""
    t = np.linspace(0, 2 * np.pi, n_time_steps)
    data = np.array([np.sin(t), np.cos(t), np.cos(t)*np.sin(t)]).T  # 2变量，n时间步

    return t, data

def perform_pod_u(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    # data shape :  (100, 2)

    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)

    print('pod U shape: ', U.shape)
    print('pod Sigma shape: ', Sigma.shape)
    print('pod VT shape: ', VT.shape)
    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前3个主要模态
    modes = U[:, :n_modes]

    print('pod modes shape: ', modes.shape)

    modal_coefficients = np.diag(Sigma[:n_modes]) @ VT[:n_modes, :]

    # 重构数据，使用所有模态
    reconstructed_data = np.dot(modes, modal_coefficients) + mean_data
    return reconstructed_data

def perform_pod_v(data):
    """执行POD并重构数据，使用SVD并选取V作为模态"""
    # 数据中心化
    mean_data = np.mean(data, axis=0)
    data_centered = data - mean_data
    
    # 使用SVD进行分解
    U, Sigma, VT = np.linalg.svd(data_centered, full_matrices=False)
    
    # 提取前几个模态和模态系数
    n_modes = 2  # 选择前2个主要模态
    modes = VT[:n_modes, :]  # 使用V的转置的前n_modes行

    print('pod_v modes shape: ', modes.shape)

    modal_coefficients = U[:, :n_modes] @ np.diag(Sigma[:n_modes])

    # 重构数据
    reconstructed_data = modal_coefficients @ modes + mean_data
    return reconstructed_data

def perform_pod_pca(data):
    """执行POD并重构数据，使用SVD避免复数问题"""
    # 数据中心化

    # pca = PCA(n_components=2)
    pca = PCA(n_components=2)
    coeff = pca.fit_transform(data)
    u_mean = pca.mean_.reshape(-1,1)
    u_modes = pca.components_.T
    
    print('u_mean: ', u_mean.shape)
    
    print('u_modes: ', u_modes.shape)
    
    print('coeff: ', coeff.shape)

    reconstructed_data = u_mean + np.dot(u_modes, coeff.T)

    return reconstructed_data.T

def compare_arrays(arr1, arr2):
    """比较两个numpy数组的统计差异"""
    if arr1.shape != arr2.shape:
        raise ValueError("Arrays must have the same dimensions")
    
    # 计算差异数组
    difference = arr1 - arr2
    
    # 计算平均值差异
    mean_difference = np.mean(difference)
    
    # 计算最大值和最小值差异
    max_difference = np.max(difference)
    min_difference = np.min(difference)
    
    # 输出结果
    print("Mean Difference:", mean_difference)
    print("Max Difference:", max_difference)
    print("Min Difference:", min_difference)


# 生成数据
n_time_steps = 100
t, data = generate_data(n_time_steps)


# data = data.T

print('data shape: ', data.shape)

reconstructed_data0 = perform_pod_u(data)

reconstructed_data1 = perform_pod_v(data)

reconstructed_data2 = perform_pod_pca(data)

compare_arrays(reconstructed_data1, reconstructed_data2)

POD和DMD的区别

“POD中的能量和DMD中的频率”

如何理解下面这句话：

“pod是按能量进行区分，dmd是按照频率进行区分”

在POD中，所谓的“能量”通常指的是数据集中的方差，它衡量的是每个模态在描述数据集的整体波动中所占的份额。在POD方法中，每个模态都会有一个对应的奇异值（在计算中来自奇异值分解或协方巧矩阵的特征值），这个奇异值的大小表示了该模态在数据中所包含的“能量”或信息量。第一个模态包含最大的能量，即方差最大，解释了数据集中最主要的波动；随后的模态所包含的能量依次减少。
DMD的关注点在于捕捉数据的时间动态，特别是周期性和增长/衰减特性。在DMD中，每个模态不仅与一个空间模式相关联，还与一个复数特征值相关联，这个复数特征值的实部和虚部分别表示该模态的增长/衰减率和振荡频率。频率这里直接对应于物理和工程中的频率概念，表示模态随时间振荡的速度；高频模态表现为快速振荡，而低频模态变化较慢。

DMD(Dynamic Mode Decomposition)

假设我们有一个时间序列数据矩阵，其中每一列是系统在某一时刻的状态向量。我们将数据划分成两个矩阵, 。它们分别包含从时间到和到的状态：

收集数据

X1 = [x1,x2,…,] (n×(m-1))

X2 = [x2,x3,…,] (n×(m-1))

计算矩阵A的近似

DMD算法寻求在时间上与两个快照矩阵相关的最佳拟合线性算子A的主导谱分解（特征值和特征向量）

(n×n)

为了找到最好的线性近似，我们使用最小二乘法求解

(n×n)

奇异值分解

(n×(m-1)) = (n×r)(r×r)(r×(m-1))

其中

r是的秩

构建低秩动态矩阵

为了得到矩阵A的一个更容易处理的表达形式，我们将X1和X2投影到由U构成的低维空间，，。

现在需要一个矩阵使得两个投影矩阵接近，

根据上一步对X1进行SVD分解的结果，带入方程可以得到：

可以得到
（r*r）

下面是另一种简单的写法，展开后和上面的结果是一样的

利用 SVD 的结果构建一个低秩近似矩阵：

（r*r）

很多公式或论文里面会把写为。

特征分解

(r*r)

其中，W是特征向量矩阵，是特征值矩阵。维度都是r*r

计算DMD模态

维度是(n*r)

这个地方需要注意下，有的地方关于模态的公式是下面这个：

这是有名的投影模态。第一个写法是精确表示，如果计算出来的是0，那么就采用第二个计算。具体的区别可以参考《数据驱动的科学和工程》p197。

数据重构

，维度是n*1

其中
，维度是r*1

“+”表示伪逆

b通常被称为初始幅度向量

表示第i个模态的振幅，可以一般是根据模态振幅的大小对DMD模态排序。

就是里面每个元素的(t-1)次方。

这样重构哪个时刻的数据就使用对应的次方

上面的公式可以改写下，也是很多论文里面经常介绍DMD会用到的：

其中

表示范德蒙矩阵

(因为渲染的原因，和显示有问题，正常显示如下图：)

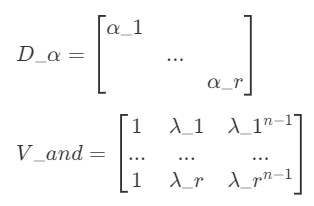
定义模态时间系数

包含了DMD的时间演化信息

预测数据

和上面的重构数据一样，假设t的范围是1<=t<=5。t=6时刻的数据为：

需要注意的是，这里我们是基于第一个时间步的数据来进行预测，如果是基于最后一个时间步的数据来进行预测，那么b会发生变化

预测未来一个时间步的数据变为：

预测未来时间步数据还有另外一种写法：

其中

注意事项

如果原始数据有20个时间步，那么t的索引范围是0-19；如果要预测未来1个时间步的数据，就是t=21，那么传入代码中的t实际应该是20
dmd方法中的模态数量选择，就是秩数量的选择。因为秩数量的选择取决于X1和X2矩阵，这两个矩阵的维度都是 n×(m-1)；而秩r的数量最多是min （n, m-1），而m一般远小于n，意味着秩做多就是m-1，代码里面重构的时候也应该注意，最多取到m-1。

参考代码如下：

import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import svd, pinv

# 这个版本的代码预测没有问题，但是重构代码有些问题，因为重构出来的值精度有问题

def dmd(X, r):
    # Step 1: SVD
    U, Sigma, Vh = svd(X[:, :-1], full_matrices=False)
    U_r = U[:, :r]
    Sigma_r = np.diag(Sigma[:r])
    V_r = Vh.conj().T[:, :r]
    
    # Step 2: 构建A_tilde
    A_tilde = U_r.conj().T @ X[:, 1:] @ V_r @ pinv(Sigma_r)
    
    # Step 3: 特征值和特征向量
    Lambda, W = np.linalg.eig(A_tilde)
    
    # Step 4: 计算DMD模式
    Phi = X[:, 1:] @ V_r @ pinv(Sigma_r) @ W
    
    return Phi, Lambda, U_r, Sigma_r, V_r, W

# DMD中时间步索引是从0开始的，原数据又20个时间步，那么索引就到19；下一个时间步的索引就是20，那么t_next就是20
def predict_next_step(Phi, Lambda, b, t_next):
    omega = np.log(Lambda)
    return (Phi @ (b * np.exp(omega * t_next))).real

# 下面的函数表示的是预测未来多个时间步的数据。
# 如果一开始的训练数据是20个时间步，那么initial_time就是20，预测几个，num_steps就是多少
def predict_future_steps(Phi, Lambda, b, initial_time, num_steps):
    omega = np.log(Lambda)
    predictions = []
    for future_time in range(initial_time , initial_time + num_steps ):
        prediction = (Phi @ (b * np.exp(omega * future_time))).real
        predictions.append(prediction)
    return np.array(predictions)

def compare_arrays(arr1, arr2):
    """比较两个numpy数组的统计差异，适用于可能包含复数的数组"""
    if arr1.shape != arr2.shape:
        raise ValueError("Arrays must have the same dimensions")
    
    # 计算差异数组的绝对值
    difference = np.abs(arr1 - arr2)
    
    # 计算平均值差异
    mean_difference = np.mean(difference)
    
    # 计算最大值和最小值差异
    max_difference = np.max(difference)
    min_difference = np.min(difference)
    
    # 输出结果
    print("Mean Difference (Magnitude):", mean_difference)
    print("Max Difference (Magnitude):", max_difference)
    print("Min Difference (Magnitude):", min_difference)

def reconstruct_data(Phi, Lambda, b, num_time_steps):
    # 计算每个模式的时间动态
    time_dynamics = np.zeros((r, num_time_steps), dtype=complex)
    for i in range(num_time_steps):
        time_dynamics[:, i] = b * np.power(Lambda, i)
    
    X_dmd = Phi @ time_dynamics
    return X_dmd

# 载入数据
# 假设X是一个(20, 1001)的数组，你需要替换这里的代码以加载你的数据
X = np.random.randn(20, 1001)  # 示例数据

# 应用DMD
r = 19  # 设置模式个数
Phi, Lambda, U_r, Sigma_r, V_r, W = dmd(X.T, r)  # 转置X，使得列变为时间步

# 计算初始b
b = pinv(Phi) @ X.T[:, 0]  # 使用转置后的第一时间步的数据

# 预测下一个时间步
predicted_field = predict_next_step(Phi, Lambda, b, X.shape[0])

reconstructed_X = reconstruct_data(Phi, Lambda, b, X.shape[0])

print("predicted_field shape: ", predicted_field.shape)

print("reconstructed_X shape: ", reconstructed_X.shape)

compare_arrays(X, reconstructed_X.T)

Jason Lin

https://gaofeng-lin.github.io/posts/f6b7c48b/

本博客所有文章除特別声明外，均采用 CC BY 4.0 reprint policy. If reproduced, please indicate source Jason Lin !

CFD

流场加速收敛论文

2024-04-23 CFD论文

流场加速收敛

时空预测

2023-12-25 research_papers

computer vision Spatiotemporal predictive learning

名词解释

weno3、weno5

CFD基础知识

网格计算

收敛

双时间步法

定长&非定常

数学知识

奇异值分解

奇异值分解和特征分解的联系

基于POD的降阶模型(版本1：从左奇异向量U提取模态)

基于POD的降阶模型(版本2，从右奇异向量V提取模态)

pod的不同实现方式

svd分解

特征分解

POD总结

POD和DMD的区别

“POD中的能量和DMD中的频率”

DMD(Dynamic Mode Decomposition)

收集数据

计算矩阵A的近似

奇异值分解

构建低秩动态矩阵

特征分解

计算DMD模态

数据重构

预测数据

注意事项

你的赏识是我前进的动力