什么是卷积
https://zhuanlan.zhihu.com/p/374458086
https://www.zhihu.com/question/22298352/answer/637156871
教科书对卷积的定义一般是:
连续形式:
离散形式:
不论是连续还是离散形式,本质上就是先将一个函数翻转,然后进行滑动叠加。
“卷”就是函数的翻转,从
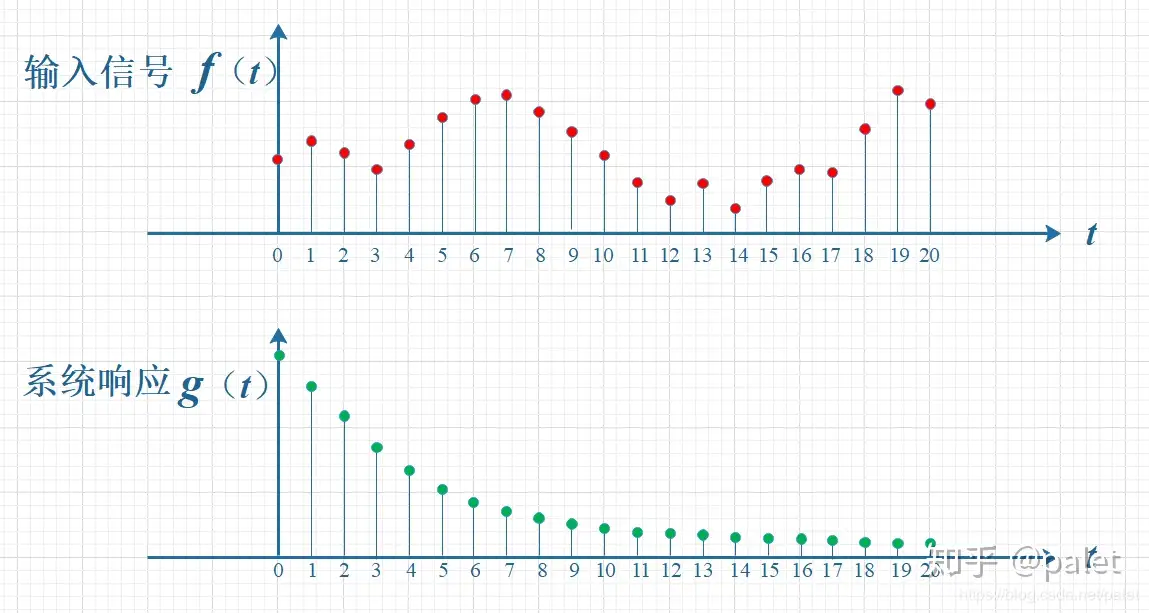
举一个例子:
计算f和g两个函数在T=10时刻的卷积值。
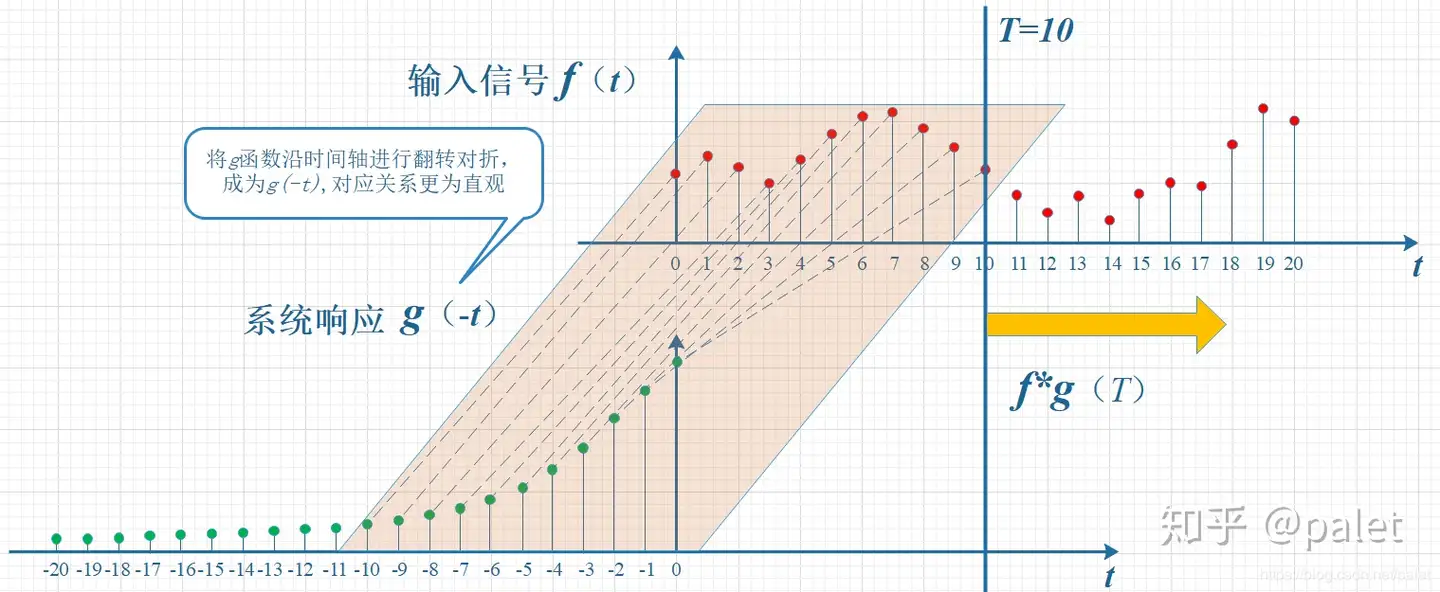
卷积的过程也是可以写为矩阵形式的,可以参考:https://www.bilibili.com/video/BV1Rj411F753/?spm_id_from=333.337.search-card.all.click&vd_source=d9f39df9d8d274edb857b2cb1c934f00
深度学习中的卷积
https://zhuanlan.zhihu.com/p/374458086
深度学习中的卷积略微有点不一样,因为并没有对卷积核进行反转(旋转180度)。当然,卷积核默认情况是对称的,所以反转也是一样。
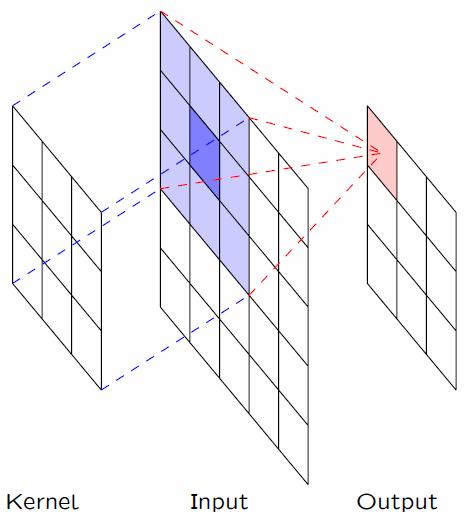
我们通过改变卷积核的数值,就可以对图像进行不同的操作,比如模糊、磨皮等。
我们可以很直观的看到,图像中的卷积,其实就是提取原始图像特征,保留了二维图像的相邻图像块的信息。
平移等变性
https://zhangting2020.github.io/2018/05/30/Transform-Invariance/
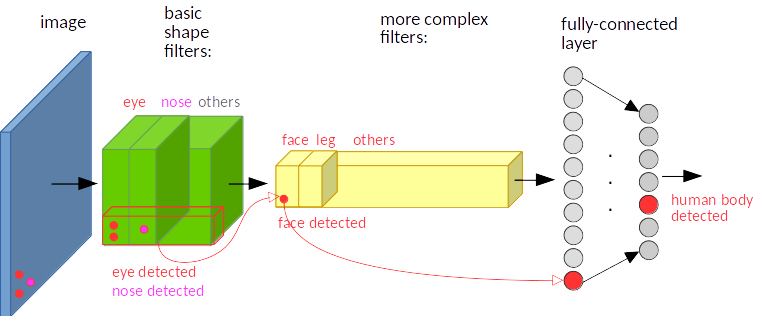
卷积是具有平移等变性,我们以目标检测为例来说明:图像中的目标不管被移动到图片的哪个位置,得到的结果(标签)应该是相同的,这就是卷积的平移等变性。
有的地方叫做平移不变性,是有点容易误解的。
之所有有这种特性,是因为卷积核在所有位置的参数是共享的,所以目标如果移动,那么相应的特征图上的表达也会移动。
卷积和傅里叶变换的联系
[CV] 通俗理解『卷积』——从傅里叶变换到滤波器 - 穆文的文章 - 知乎
https://zhuanlan.zhihu.com/p/28478034
时域卷积=频域相乘
假设两个时域信号f1和f2『卷积』的结果是f3,则f3的频谱,是f1的频谱函数和f2的频谱函数,对应频率『相乘』的结果。
图像卷积里面,我们一般会使用多个卷积核,那么会得到多个特征图,相当于提取了多个特征,比如模糊化、边缘检测等。
当我们把图像跟多种卷积核作用时,就能得到不同频段的信号,这也就是卷积神经网络中,『卷积层』的本质作用。所以,图像卷积的本质,就是提取图像不同频段的特征。



