快速总结

基础

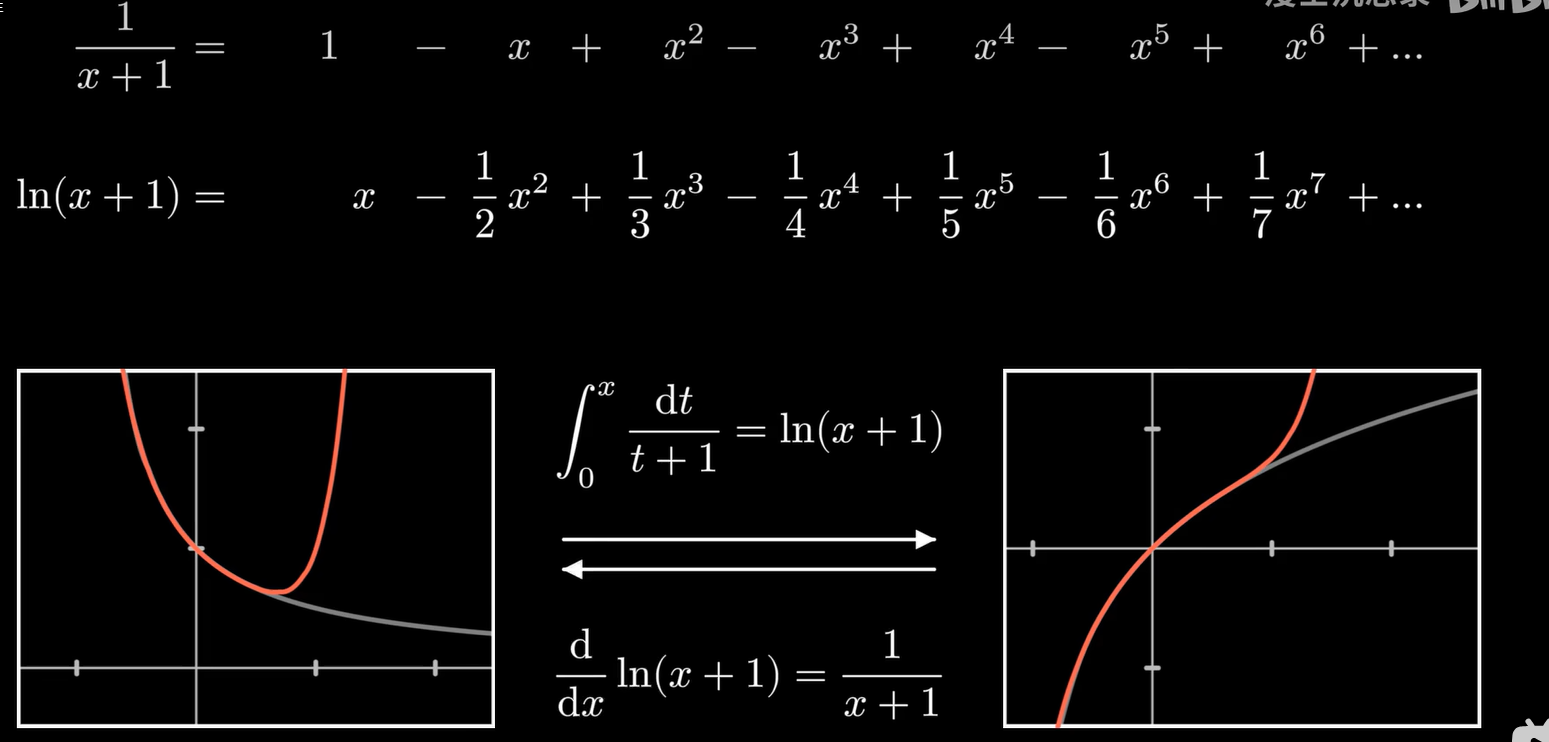
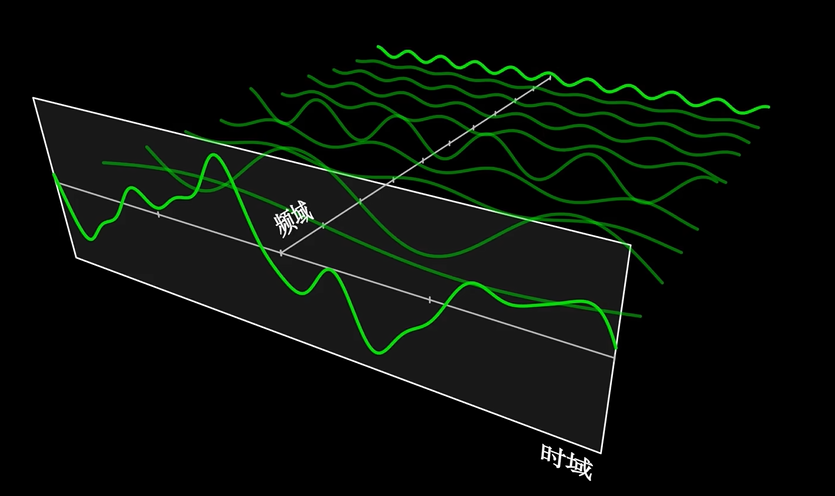
傅里叶变换是把时域数据分解为频域数据的，假设输入是周期函数，具体来说如下图所示：

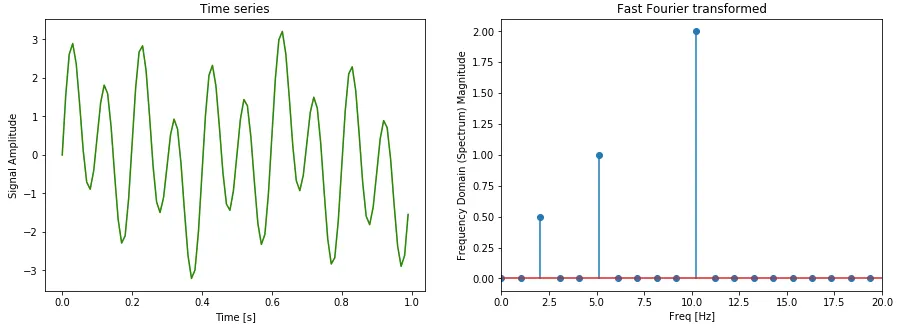
左边的是时域图，右边的是频域图。

频域图横轴是频率（1秒内周期重复的次数。如果重复两次就是2HZ，重复一次就是1HZ），纵轴是振幅。我们对振幅不为0的频率使用反向傅里叶变化，就可以得到sin/cos图像：

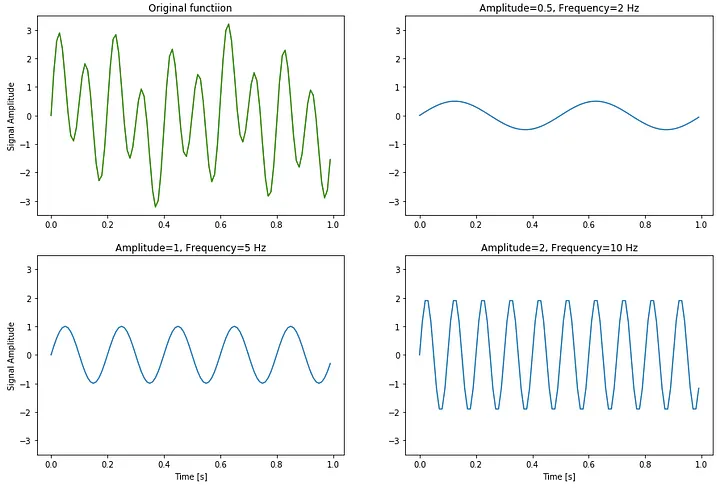
也就是说，原始时域数据，可以被分解为多个sin/cos图像的叠加。

而还原得到的sin/cos图像的振幅和频率，也和频率图对应的结果一样。

HZ越高就是高频，HZ越低就是低频，这里不要和振幅混淆。也就是说，坐标轴左边的是低频，右边的是高频。我们经常说高频是噪声，就是因为它的波动无序，很混乱，周期短。

虽然上面的图只显示了正频率和0频率，但傅里叶变化计算出来的其实是具有负频率的，只不过正频率和对应负频率的幅值是相同的，只是画了正频率的一部分。但是在实际反向傅里叶变换的使用，也是会运用到负频率的结果。也就是说，还原的时候，所有的频率都会使用到，包括0频率。

对与0频率来说，是非常重要的。0Hz 代表的是直流分量（DC Component），也就是整段数据的平均值。但是如果使用了RevIN归一化（时序预测通常这么做），那么0Hz 的振幅理论上应该接近于 0。如果不归一化，0Hz 的振幅通常是最大的。

如果输入是离散的数据，比如说是8个值，那么傅里叶变化会得到8个复数，这8个复数的模长就是对应频率的振幅。

关于正负对称可以多说两句。

如果输入是偶数，假设为8，出去0HZ，还剩下7个。
Index 1, 2, 3: 正频率部分
Index 5, 6, 7: 负频率部分（对应 -3, -2, -1）
Index 4 (Nyquist Frequency): 是一半采样率的位置 ()。它也没有对称的。
也就是说，如果输入时偶数，那么打印出来的频率图是[N/2+1]。

如果输入是奇数，假设为9，那么除去0HZ，剩下的就是对称的。

代码

python中我们一般使用rfft来进行傅里叶变化，准确的是快速傅里叶变化。rfft得到的是复数，只有正频率部分的结果。

网上视频

https://www.bilibili.com/video/BV1eUHjzgEAd/?spm_id_from=333.337.search-card.all.click&vd_source=d9f39df9d8d274edb857b2cb1c934f00
建系（建立坐标系），有了坐标系，点的位置变成了数字，曲线变成了方程，交点变成了解方程，按部就班就能解决几何问题。

坐标系的本质是用坐标轴分解位置，坐标轴的本质是基底向量。笛卡尔坐标系中的基底向量就是u=(1 0), v=(0 1)，如下图所示：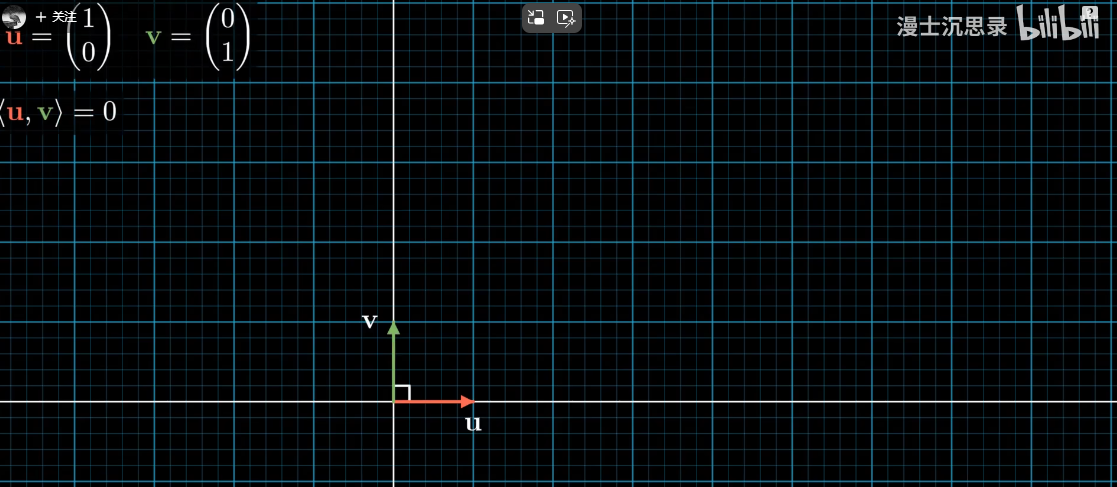

一旦明确了基底向量，就拥有一套双向翻译体系。

用数字线性组合基底，得到这个坐标所对应的抽象的几何空间位置；

反过来，只要能把一个抽象的向量在基底下分解成线性组合，只需要把这些组合的系数拼在一起，就能得到坐标：

向量和坐标之间最重要的对应关系：线性相加
两个抽象的向量相加，得到和向量的坐标，一定是两者坐标一位位对应加起来的。

傅里叶变化要分析的向量是所有的周期函数

傅里叶变化选择的基底是一系列不同周期的正余弦函数。之所以选这个，是因为正弦函数是振动的基本单元，求导，积分都很方便。所以拿来做基底。

从坐标翻译到向量时，把每个单项式乘以坐标的各个系数，再加到一起，就还原了原本的多项式。

从基底分解来得到函数之间的积分、求导关系。

把多项式在单项式的基底下分解的时候，只需要盯着多项式每一项的系数，就能自动得到坐标。

但如果给的是一些乱七八糟的波，如何知道要用几倍的cosx 加几倍的sinx得到这个波呢？

在抽象的向量和抽象的坐标系里，想要找到坐标对应的系数，让基底线性组合得到想要的向量，需要一套抽象的方法。这个问题的答案就是内积。

在笛卡尔坐标系里面找一个点的横坐标，向x轴做垂线，找交点就好，但是到了更抽象的空间里，我们很难定义垂线和交点这种几何背景过于浓厚的概念。取而代之的是用内积来找坐标。

满足基本条件都可以当作基底

用基底向量组合空间中任意一个向量平常

它的基底是所有形如sinnx cosmx的周期函数，通过线性组合他们，可以表示出几乎所有周期为2pi的函数，比如方波。

傅里叶变换把函数变成了坐标，有什么用？

意义：给出了另一个看待函数的视角

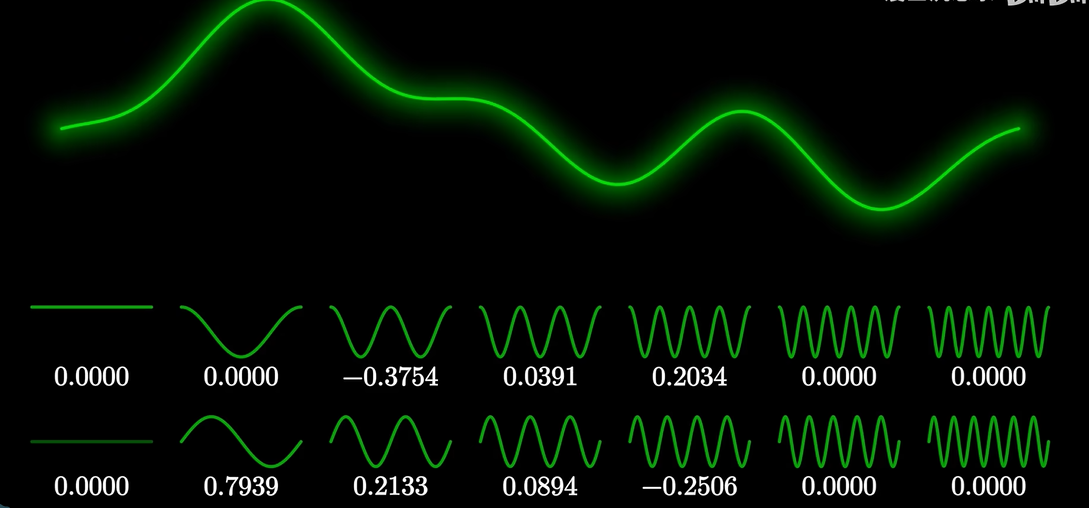
各个不同振动频率所对应的能量大小，每一个正弦波前面的系数，就表示这个正弦周期的振动有多显著，将这些振动系数一一列出，就可以还原的函数形状。这些系数有个专业的名词，叫频谱。

频率小周期大的基底对应的叫做低频区；频率高周期小的基底对应的叫做高频区。

信号处理领域的用法：

语言去噪：信号在频谱中会显示不同频率的成分，而噪声，往往对应着特定的频率区域，只需要在频谱中降低或删除这些能量，就能让语言清晰起来。

流程

具体流程如下：

输入：拿进去一个长度为的时间序列（例如）。
执行 FFT：。
取模（Amplitude）：计算结果的振幅。
- 这时你会得到一个列表，下标是频率，值是强度。
Top-k 筛选：找到振幅最大的前个频率点（比如）。
- 含义：这些是数据里最“强”的节奏。
频率转周期（关键公式）：论文中经常出现这个公式：。例子：假设你输入 100 个点 ()。FFT 告诉你频率的地方振幅最大。解读：说明这 100 个点里，有个波形重复了 4 次。周期：。也就是说，每隔 25 个点，数据就会重复一次规律。